그래프란?
수학에서, 좀 더 구체적으로 그래프 이론에서 그래프란 객체의 일부 쌍(pair)들이 '연관되어' 있는 객체 집합 구조를 말한다. 그래프를 표현하는 방법에는 크게 인접 행렬(adjacency matrix)과 인접 리스트(adjacency list)의 2가지 방법이 있는데, 두 방법 모두 방향 및 무방향 그래프에 적용할 수 있다. 인접 리스트 방법이 작은 밀도 그래프(|E|가 |V|2보다 훨씬 작은 그래프)에 대해 효율적이다. 반면, |E|와 |V|2가 거의 비슷한 높은 밀도 그래프에서는 주어진 두 정점을 연결하는 간선이 있는지 빠르게 확인할 필요가 있을 때는 인접행렬 표현법을 더 선호한다.
인접 리스트의 특징
인접 리스트는 메모리 양이 ø(V+E)라는 바람직한 특성을 가진다. 또한 각 간선이 가중치 함수로 주어지는 가중치 그래프를 표현하는 데도 쉽게 적용할 수 있다. 인접 리스트의 잠재적 단점은 주어진 간선이 그래프에 있는지를 확인하기 위해 인접 리스트에서 v를 검색하는 것보다 빠른 방법을 제공하지 못한다는 것이다. 인접행렬로 표현하는 것은 이런 단점은 해결하지만 점근적으로 더 많은 메모리를 사용해야 한다.
인접행렬의 특징
인접행렬로 그래프를 표현할 때는 간선 개수와 상관없이 ø(V2)의 메모리가 필요하다. 인접행렬은 주대각선을 따라 대칭이다. 무방향 그래프의 인접행렬 A는 그 자신의 전치행렬과 같다. 즉 A = AT이다. 어떤 응용에서는 인접행렬의 대각선과 또는 그 위쪽에 있는 원소만 저장하게 하여 그래프를 저장하기 위해 필요한 메모리를 거의 절반 정도로 줄일 수 있다. 인접행렬에서는 가중치 w를 해당 행과 열의 원소로 넣어주어 가중치를 표현할 수 있다. 인접행렬이 공간적인 면에서 표현이 더 단순하므로 그래프가 어느정도 작은 경우에는 인접행렬을 더 선호할 수도 있다. 게다가 가중치가 없는 그래프에 대해 행렬 원소마다 한 비트만 필요하다는 장점도 있다.
속성을 표현하는 방법
정점이나 간선에 대한 속성을 저장하고 접근하는 데 최상의 방법은 존재하지 않는다. 주어진 상황의 사용 프로그래밍 언어, 구현 알고리즘, 그래프 사용 방법이 다를 가능성이 높기 때문이다. 만약 인접 리스트를 이용한다면, 부가적인 배열을 이용해 그 배열의 원소에 저장할 수 있을 것이다. 객체 지향 프로그래밍 언어에서는 정점에 대한 속성을 Vertex클래스의 서브 클래스에서 인스턴스 변수로 표현할 수 있다.
그래프 순회(Graph Traversals)
그래프 순회란 그래프 탐색(search)이라고도 불리우며 그래프의 각 정점을 방문하는 과정을 말한다. 크게 깊이 우선 탐색(Depth-First Search)과 너비 우선 탐색(Breadth-First Search)의 2가지 알고리즘이 있다. DFS는 프랑스의 수학자 찰스 피에르 트레모가 미로 찾기를 풀기 위한 전략을 찾다가 고안한 것으로 알려져 있으며, 일반적으로 BFS에 비해 더 널리 쓰인다.
DFS는 주로 스택으로 구현하거나 재귀로 구현하며, 이후에 살펴볼 백트래킹을 통해 뛰어난 효용을 보인다. 반면, BFS는 주로 큐로 구현하며, 그래프의 최단 경로를 구하는 문제 등에 사용된다. 예를 들어, 다익스트라 알고리즘으로 최단 경로를 찾는 문제에서 BFS로 구현할 수 있다.
그래프를 인접 리스트로 표현
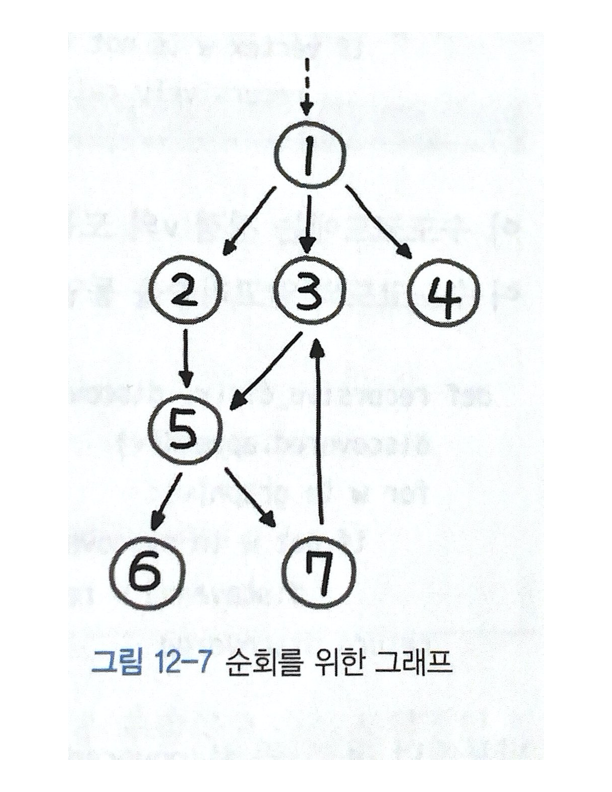
인접 리스트는 출발 노드를 키로, 도착 노드를 값으로 표현할 수 있다. 도착 노드는 여러 개가 될 수 있으므로 리스트 형태가 된다. 파이썬의 딕셔너리 자료형으로 다음과 같이 나타낼 수 있다.
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}이 딕셔너리를 입력값으로 각각 DFS, BFS로 구현해보자.
DFS(깊이 우선 탐색)
DFS는 일반적으로 스택으로 구현하며, 재귀를 이용하면 좀 더 간단하게 구현할 수 있다. 코딩 테스트 시에도 재귀 구현이 더 선호되는 편이다.
재귀 구조로 구현
Pseudo Code
DFS(G, v)
lavel v as discoverd
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G, w)이 수도코드에는 정점 v의 모든 인접 유향(directed) 간선들을 반복하라고 표기되어 있다.
Code
def recursive_dfs(v, discovered=[]):
discovered.append(v)
for w in graph[v]:
if not w in discovered:
discovered = recursive_dfs(w, discovered)
return discovered방문했던 정점, 즉 discovered를 계속 누적된 결과로 만들기 위해 리턴하는 형태만 받아오도록 처리했을 뿐 다른 부분들은, 예를 들어 변수명까지 동일하게 수도코드와 맞춰서 작성해 봤다. 위의 그래프를 입력값으로 한 탐색 결과는 다음과 같다.
>>> f'recursive dfs: {recursive_dfs(1)}' 'recursive dfs: [1, 2, 5, 6, 7, 3, 4]'
스택을 이용한 반복 구조로 구현
Pseudo Code
DFS-iterative(G, v)
let S be a stack
S.push(v)
while S is not empty do
v = S.pop()
if v = is not labeled as discovered then
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
S.push(w)스택을 이용해 모든 인접 간선을 추출하고 다시 도착점인 정점을 스택에 삽입하는 구조로 구현되어 있다.
Code
def iterative_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered이와 같은 반복 구현은 , 앞서 코드가 길고 빈틈없어 보이는 재귀 구현에 비해 우아함은 떨어지지만, 좀 더 직관적이라 이해하기는 훨씬 더 쉽다. 실행 속도 또한 더 빠른 편이다. 그래프를 입력한 탐색 결과는 다음과 같다.
>>> f'iterative dfs: {iterative_dfs(1)}' 'iterative dfs: [1, 4, 3, 5, 7, 6, 2]
똑같은 DFS인데 순서가 다르다. 앞서 재귀 DFS는 사전식 순서(lexicaographical order)로 방문한 데 반해 반복 DFS는 역순으로 방문했다. 스택으로 구현하다 보니 가장 마지막에 삽입 된 노드부터 꺼내서 반복하게 되고 이경우 인접 노드에서 가장 최근에 담긴 노드, 즉 가장 마지막부터 방문하기 때문이다. 인접 노드를 한꺼번에 추가하는 형태이기 때문에, 자칫 BFS가 아닌가 하고 헷갈릴 수 있지만 깊이 우선으로 탐색한다는 점에서 DFS가 맞다.
BFS(너비 우선 탐색)
BFS는 가장 단순한 그래프 검색 알고리즘 중 하나로, 중요한 그래프 알고리즘들의 원형이다. 프림(prim)의 최소 신장 트리 알고리즘과 다익스트라의 단일 출발점 최단 경로 알고리즘은 BFS와 비슷한 아이디어를 사용한다. DFS보다 쓰임새는 적지만, 최단 경로를 찾는 알고리즘 등에 매우 유용하게 쓰인다.
BFS에서 주어진 입력 그래프 G = (E, V)에 대해 수행시간을 분석해보면 큐에 연산을 하는 데 걸리는 총 시간은 O(V)이므로, 인접 리스트를 스캔하는 데 걸리는 시간은 O(E)이다. 초기화 하는 데 필요한 일은 O(v)이므로 BFS를 수행하는 데 걸리는 총 시간은 O(V+E)이다. 즉, 그래프 G의 인접 리스트 표현의 크기에 선형적으로 비례하는 시간이 걸린다.
큐를 이용한 반복 구조로 표현
Pseudo Code
BFS(G, start_v)
let Q be a Queue
label start_v as discovered
Q.enqueue(start_v)
while Q is not empty do
v := Q.dequeue()
if v is the goal then
return v
for all edges from v to w in G.adjacenctEdges(v) do
if w is not labeled as discovered then
lavel w as discovered
w.parent := v
Q.enqueue(w)모든 인접 간선을 추출하고 도착점인 정점을 큐에 삽입하는 수도코드다.
Code
def iterative_bfs(start_v):
discovered = [start_v]
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered그래프를 입력값으로 한 탐색 결과는 다음과 같다.
>>> f'iterative bfs: {iterative_bfs(1)}' 'iterative bfs: [1, 2, 3, 4, 5, 6, 7]'
BFS의 경우 단계별 차례인 숫자 순으로 실행됐으며, 1부터 순서대로 각각의 인접 노드를 우선으로 방문하는 너비 우선 탐색이 잘 실행됐음을 확인할 수 있다.
재귀 구현 불가
BFS는 재귀로 동작하지 않는다. 큐를 이용하는 반복 구현만 가능하다.
백트래킹(Backtracking)
백트래킹은 해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기(백트랙, backtrack)해 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제(constraint satisfaction problems)에 특히 유용하다.
DFS를 이야기하다 보면 항상 백트래킹이라는 단어가 함께 나온다. 백트래킹은 DFS보다 좀 더 광의의 의미를 지닌다. 백트래킹은 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다는 데서 유래했다. DFS와 같은 방식으로 탐색하는 모든 방법을 뜻하며, DFS는 백트래킹의 골격을 이루는 알고리즘이다.
백트래킹은 주로 재귀로 구현하며, 알고리즘마다 DFS 변형이 조금씩 일어나지만 기본적으로 모두 DFS의 범주에 속한다. 운이 좋으면 시행착오를 덜 거치고 목적지에 도착할 수 있지만 최악의 경우 모든 경우를 다 거친 다음에 도착할 수 있기 때문에 브루트 포스와 유사하다. 하지만 한번 방문 후 가능성이 없는 경우에는 즉시 후보를 포기한다는 점에서 매번 같은 경로를 방문하는 브루트 포스보다는 훨씬 더 우아한 방식이라 할 수 있다.
가능성이 없는 후보를 포기하고 백트래킹 하는 동작을 트리의 가지치기(pruning)라고 하며, 이처럼 불필요한 부분을 일찍 포기한다면 탐색을 최적화 할 수 있기 때문에, 가지치기는 트리의 탐색 최적화 문제와도 관련이 깊다.
제약 충족 문제(Constraint Satisfaction Problems)
제약 충족 문제란 수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제를 일컫는다.
백트래킹은 CSP를 풀이하는 데 필수적인 알고리즘이다. 가지치기를 통해 제약 충족 문제를 최적화 하기 때문이다. 특히 CSP는 인공지능이나 경영 과학 분야에서도 심도 있게 연구되고 있으며, 합리적인 시간 내에 문제를 풀기 위해 휴리스틱과 조합 탐색 같은 개념을 함께 결합해 문제를 풀이한다. 스도쿠, 십자말 풀이, 8퀸 문제, 4색 문제 같은 퍼즐 문제와 배낭 문제, 문자열 파싱, 조합 최적화 문제 등이 모두 CSP에 속한다.
