도입

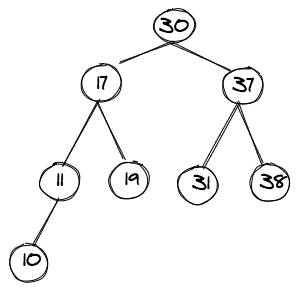
트리 구조란 그프의 일종으로, 한 노드에서 시작해서 다른 정점들을 순회하여 자기 자신에게 돌아오는 순환이 없는 연결 그래프라고 한다.

이전에 작성했던 스택, 큐 자료구조는 선형 자료구조이다. 반면 트리 자료구조는 비선형 자료구조이다. 위의 사진을 보면 알 수 있다.

트리는 계층적 관계를 표현하는 자료구조이다.

트리(tree)라는 이름은 루트 노드를 중심으로 뻗어나가는 모습이 나무의 구조와 비슷하여 붙여지게 되었다고 한다.

트리 관련 용어

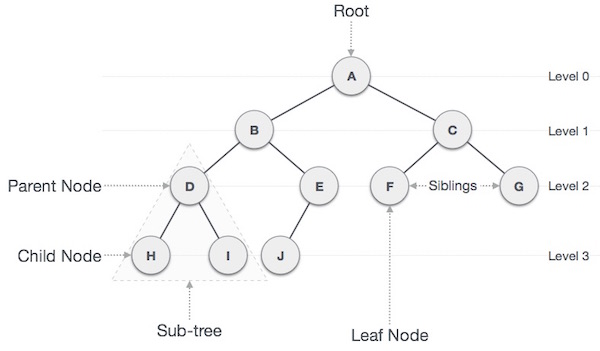
• 노드 : node
  트리의 구성 요소에 해당하는 A,B,C,D,E,F,G,H,I,J와 같은 요소

• 간선 : edge
  노드와 노드를 연결하는 연결선

• 루트 노드 : root node
  트리 구조에서 최상위에 존재하는 A와 같은 노드

• 단말 노드 : terminal node
  아래로 또 다른 노드가 연결되어 있지 않은 H,I,J,F,G와 같은 노드
  단말 노드는 나무의 구조상 잎에 해당한다고 하여 '잎사귀 노드(leaf node)'라고도 불린다

• 내부 노드 : internal node
  단말 노드를 제외한 모든 노드
  단말 노드가 아니라는 뜻에서 '비단말 노드(nonterminal node)'라고도 불린다

• 부모(parent), 자식(child), 형제(sibling) 노드
  노드 간의 관계를 부모, 자식, 형제 관계로 표현할 수 있다
  노드의 관계는 상대적이어서 부모 노드이면서 동시에 자식 노드일 수 있다. 예를 들어서 B는 A의 자식 노드이지만 동시에 D,E의 부모 노드이다.

• 서브 트리(sub tree)
  큰 트리에 속하는 작은 트리를 서브 트리라고 한다

• 레벨(level)
  트리의 각 층별로 숫자를 매기고 이를 트리의 레벨이라고 한다. 트리의 레벨은 0부터 시작해서 아래로 갈 수록 숫자가 커진다.

• 높이(height)
  트리의 레벨이 0부터 시작하기 때문에 트리의 최고 레벨을 트리의 높이라고 한다. 위 사진의 트리의 최고 레벨은 3이기 때문에 이 트리의 높이는 3이다.

이진 트리(Binary Tree)

이진 트리는 다음의 두 조건을 만족하는 트리이다.

• 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
• 나뉘어진 두 서브 트리도 모두 이진 트리이어야 한다.

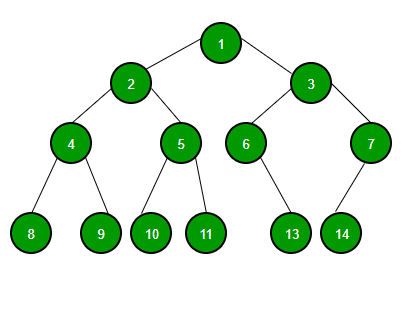
노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면, 공집합(empty set) 노드가 존재하는 것으로 간주한다. 공집합 노드도 이진 트리의 판단에 있어서 노드로 간주한다.

그렇기 때문에 위의 사진도 이진 트리이다. 8~14번 노드와 같은 leaf node의 밑에도 공집합 노드가 존재한다고 볼 수 있고, 6번과 7번 노드의 자식 노드로 공집합 노드가 있다고 볼 수 있기 때문에 위의 조건을 만족하기 때문이다.

위와 같은 트리도 이전 트리에서의 논리를 적용하면 이진 트리임을 알 수 있다.

이진 트리라는 이름에서 연상되는 트리보다 더 넓은 범위의 트리가 이진 트리에 속한다는 것을 알 수 있다.

특수한 경우의 이진 트리가 있다. 바로 포화 이진 트리(Full Binary Tree)와 완전 이진 트리(Complete Binary Tree)이다.

포화 이진 트리(Perfect Binary Tree)

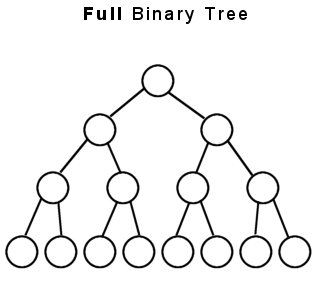
위의 이진 트리는 모든 레벨이 꽉 차 있다. 따라서 노드를 더 추가하려면 레벨을 높여야 한다. 이처럼 모든 레벨이 꽉 찬 이진 트리를 포화 이진 트리라고 한다.

완전 이진 트리(Complete Binary Tree)

완전 이진 트리란 노드가 위에서 아래로, 그리고 왼쪽에서 오른쪽의 순서대로 채워진 트리이다. 위 사진의 트리가 완전 이진 트리이다.

이진 트리의 구현

이진 트리는 배열을 기반으로 구현할 수도 있고, 연결 리스트를 기반으로 구현할 수도 있다.

배열 기반 이진 트리

만약 트리가 완성된 이후부터는 그 트리를 대상으로 매우 빈번한 탐색이 이루어진다면 배열을 기반으로 이진 트리를 구현하는 것이 좋다. 배열의 특성상 연결 리스트와 비교하여 탐색 속도가 빠르기 때문이다.

힙(heap)이라는 자료구조는 배열을 기반으로 구현한 이진 트리를 사용한다.

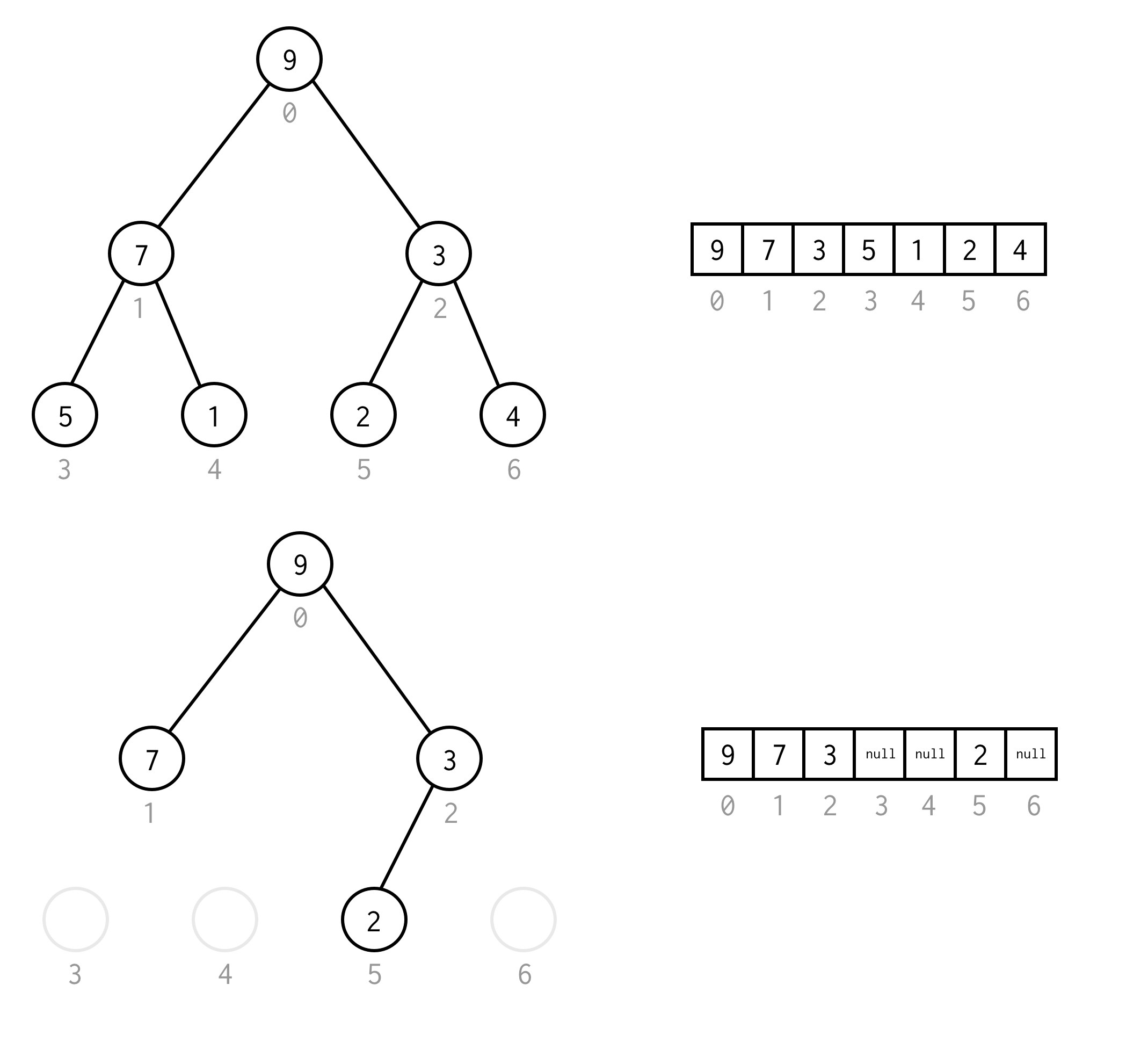
배열을 이용해서 이진 트리를 구현하기 위해서는, 우선 각 노드에 번호를 부여한다. 이때 부여한 번호가 각 노드의 데이터가 저장되어야 할 배열의 인덱스 값을 의미한다. 번호를 부여한 뒤에는 번호에 해당하는 배열의 자리에 노드의 데이터를 저장한다.

연결 리스트 기반 이진 트리

연결 리스트를 이용하여 이진 트리를 구현하면 위 그림과 같다. 연결 리스트의 구성 형태가 트리와 일치하는 것을 알 수 있다.

이진 트리의 ADT

• BTreeNode* MakeBTreeNode(void) : 이진 트리 노드를 생성하여 그 주소 값을 반환한다.
• BTData GetData(BTreeNode* bt) : 노드에 저장된 데이터를 반환한다.
• void SetData(BTreeNode* bt, BtData data) : 매개변수 data를 이용해서 전달된 데이터를 노드에 저장한다.
• BTreeNode* GetLeftSubTree(BTreeNode* bt) : 왼쪽 서브 트리의 주소 값을 반환한다.
• BTreeNode* GetRightSubTree(BTreeNode* bt) : 오른쪽 서브 트리의 주소 값을 반환한다.
• void MakeLeftSubTree(BTreeNode* main, BTreeNode* sub) : 왼쪽 서브 트리를 연결한다.
• void MakeRightSubTree(BTreeNode* main, BTreeNode* sub) : 오른쪽 서브 트리를 연결한다.

이진 트리의 순회(Traversal)

이진 트리를 대상으로 하는 대표적인 순회의 방법은 세 가지가 있다. 루트 노드의 방문 순서에 따라서 순회 방법이 나뉜다.

• 전위 순회(Preorder Traversal) - 루트 노드를 먼저 방문

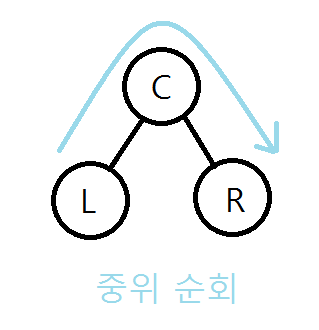
• 중위 순회(Inorder Traversal) - 루트 노드를 중간에 방문

• 후위 순회(Postorder Traversal) - 루트 노드를 마지막에 방문

높이가 2 이상인 이진 트리는 루트 노드는 다음과 같이 서브 트리를 방문하는 식으로 순회를 진행하면 된다.

예) 높이가 2 이상인 이진 트리의 중위 순회
1단계 : 왼쪽 서브 트리의 순회
2단계 : 루트 노드의 방문
3단계 : 오른쪽 서브 트리의 순회
(서브 트리에서의 순회도 1~3단계를 반복하면 된다. 재귀적이다.)

이진 트리의 활용

이진 트리는 다음과 같은 곳에서 활용할 수 있다.

• 수식 트리(Expression Tree)
• 허프만 코딩 트리(Huffman coding tree)
• 이진 검색 트리(Binary Search Tree,BST)
• 우선 순위 큐(Priority Queue)