[Quantum Computing] Week 1 : 선형대수 review-1

1. 학습 배경

좋은 기회로, 대학원 재학생 및 졸업생 분들과 함께 양자 컴퓨터의 기초부터 차근차근 배우는 스터디에 참가하게 되었다!! 💪🏻💪🏻
이번 스터디 주제인 양자 컴퓨터 분야는, 양자 역학을 활용하는 컴퓨터 하드웨어 및 알고리즘을 비롯한 특수 기술을 사용하여 기존 컴퓨터나 슈퍼컴퓨터가 해결할 수 없거나 충분히 빠르게 해결할 수 없는 복잡한 문제를 해결하도록 고안되었다.

특히, 양자 컴퓨터의 기초가 되는 양자 알고리즘은 기존 컴퓨터의 로직으로 해결하기 어려운 복잡한 문제에 대해 다차원 계산 공간을 만드는 새로운 접근 방식을 취함으로서 AI/머신러닝 등 고성능 컴퓨터 자원을 필요로 하는 많은 Task를 해결하는데 활발히 활용되고 있어 더욱 관심이 생기게 된 분야이다.

아래는 이번 스터디의 목표와, 공부하고자 한 주요 내용들을 정리해보았다.

🎯 목표

• 양자 컴퓨터의 기본 개념과 원리를 이해
• 양자 컴퓨팅의 기초적인 기술을 학습
• 관련 책, 강의, 논문 등을 활용하여 심층학습 진행

📚스터디 주요 내용📚

• 양자 컴퓨터의 기본 개념과 양자역학의 기초 개념
• 양자 컴퓨터의 수학적 기초인 선형대수학 이해
• 양자 컴퓨터의 핵심 구성 요소인 qubit, 양자 게이트 및 작동원리
• Shor 알고리즘, Grover 알고리즘 등 주요 양자 알고리즘의 구조와 작동 원리 학습
• Qiskit과 같은 도구를 사용하여 실제 양자 컴퓨터에서 실습 진행

전체적으로 위와 같은 방향으로 함께 총 8명이서 스터디를 진행하게 되었고, 가장 처음으로 수학적 기초가 되는 선형대수학의 기초를 유튜브에 탑재된 강의 [서울대학교 공과대학] 양자 컴퓨팅 및 정보의 기초 를 활용하여 공부하였다.

Week 1 : 선형대수 Review 1

Vector

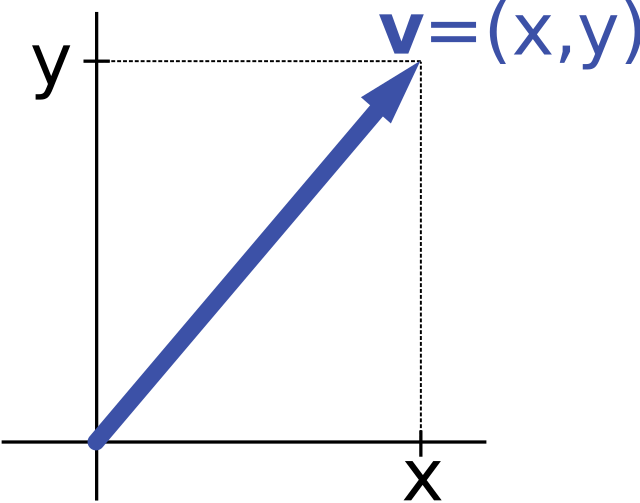
• 크기(또는 길이)와 방향을 가지는 화살표 같은 개념
• 예를 들어, 시작점이 (0,0)이고 끝점이 (x,y) 일때 시작점 -> 끝점으로 가는 위 화살표가 벡터라고 할 수 있다.

선형 벡터 공간 (Linear Vector Space)

• 선형 벡터 공간 (Linear Vector Space)은 벡터라 불리는 객체들의 집합
• 단순히 집합이 형성되면 되는 것이 아니라, 이 집합에서 두 가지 연산(벡터 덧셈, 스칼라 곱)이 충족되어야 한다
  • Vector Addition(벡터의 덧셈) : 두 벡터를 더할 수 있어야 함. 예를 들어, ∣V⟩와 ∣W⟩라는 두 벡터가 있을 때, 이들의 합도 여전히 같은 벡터 공간 안에 속하는 새로운 벡터 ∣V⟩+∣W⟩를 만들 수 있다
    • 덧셈의 교환법칙 : ∣V⟩+∣W⟩=∣W⟩+∣V⟩
    • 덧셈의 결합법칙 : (∣V⟩+∣W⟩)+∣Z⟩=∣V⟩+(∣W⟩+∣Z⟩)
    • Null Vector : 벡터 ∣0⟩|는 'Null Vector'라 불리며, 어떤 벡터에 더해져도 그 벡터를 바꾸지 않는다. 즉, ∣V⟩+∣0⟩=∣V⟩. 또한 벡터 ∣0⟩|는 유일하게 존재함.
    • 벡터의 덧셈에 대한 역원: 각 벡터 ∣V⟩에는 덧셈에 대한 역벡터 −∣V⟩가 존재하여 ∣V⟩+(−∣V⟩)=∣0⟩을 만족한다.
  • Multiplication by scalars(스칼라 곱) : 스칼라(숫자)를 아래 법칙을 만족하면서 벡터에 곱할 수 있다.
    • Closure : 벡터를 더하거나 스칼라를 곱한 결과는 여전히 같은 벡터 공간 안에 있어야 한다. 즉, ∣V⟩+∣W⟩ ∈ V.
    • 스칼라 곱의 분배법칙 : a(∣V⟩+∣W⟩) = a∣V⟩+a∣W⟩
    • 스칼라 곱의 결합법칙 : a(b∣V⟩) = (ab)∣V⟩
    • 어떤 벡터를 0벡터와 곱하면 항상 0벡터이다. 즉, 0∣V⟩ = ∣0⟩ 만족
• |B⟩ : ket
• ⟨A| : bra
  
• ⟨A|B⟩ : braket
  • ad+be+cf 로 계산됨.

Field

• 벡터 공간에서 벡터에 곱해지는 필드란 일반적으로 실수나 복소수로, 스칼라(a,b,…)와 거의 유사하게 받아들여진다. 필드가 복잡하다면, 복잡한 벡터 공간을 가지게 되는 것! 양자컴퓨터에서의 스칼라는 Complex number(복소수)가 보통 활용된다.
• field = scalar

선형 독립(Linear Independent)

• 벡터 공간 내에 여러가지 벡터들이 존재한다. 벡터들의 선형 결합이 0이 되는 경우에 이 상수 계수들이 전부 0인 경우에만 선형 결합이 0이 되면, 선형 독립이라고 한다.
  • 즉, a|A⟩+b|B⟩+c|C⟩ = 0 을 만족하는 a,b,c가 오직 0 뿐일때 Linear Independent(선형 독립)이라고 함.
  • a,b,c가 모두 0일때 외에 다른 case가 존재하면 Linear dependent(선형 종속)이라고 함.

차원(Dimension)

• 벡터 공간에서 존재할 수 있는 선형 독립 벡터들의 최대 개수
  • 2차원 공간에서는 최대 2개의 선형 독립 벡터가 있을 수 있다. 예를 들어, 벡터 (1,0)과 (0,1)는 선형 독립 벡터이며, 이 두 벡터로 2차원 평면의 모든 벡터를 생성할 수 있다.
  • 3차원 공간에서는 (1,0,0), (0,1,0), (0,0,1))가 선형 독립 벡터이며, 세 벡터로 3차원 공간을 채울 수 있다.
  • 2x2 Matrix 공간에서는 독립적인 값(성분)이 4개이므로 2x2 행렬이 형성하는 벡터 공간은 4차원이다.
• n차원 공간에 속한 모든 벡터는 n개의 선형독립벡터의 선형 결합으로 나타낼 수 있다.
  • |V⟩ = a|A⟩+b|B⟩+c|C⟩+...

기저(Basis)

• n차원 공간에 존재하는 n개의 선형 독립 벡터들로 이루어진 집합
• 벡터 공간에서 basis는 여러 개 존재할 수 있다

벡터의 성분(Component of Vector)

• 어떤 벡터를 basis에 계수(coefficients)를 곱하여 표현할 때, 해당 계수를 벡터의 성분이라고 함.
  • 예시 : (2, 3) 벡터에서 (1, 0)과 (0, 1)을 기저로 사용할 때, (2,3) 벡터의 성분은 각각 2와 3 이다.
• 이와 같은 원리로, 벡터의 성분은 basis가 바뀔때마다 다른 성분으로 나타날 수 있다.
• 단, 어떤 벡터를 표현하는 basis가 동일하다면 해당 벡터의 component는 유일(unique)하게 존재한다. 이는 아래와 같이 간단하게 증명 가능
  • |V⟩ = a1|A⟩+a2|B⟩ = b1|A⟩+b2|B⟩ 에서,
  • (a1-b1)|A⟩+(a2-b2)|B⟩ = 0 이므로
  • a1 = b1, a2 = b2 이다.

Inner Product Spaces

• 내적의 정의

  def inner_product(A, B):
      if len(A) != len(B):
          raise ValueError("Vectors must be of the same length")
      return sum(a * b for a, b in zip(A, B))

• 내적연산의 일반적인 요구조건 4가지
  • 내적의 결과는 number 이다!
  • 내적에서 연산 순서를 바꾸면 켤레 복소수가 됨. 즉, 복소수의 실수 부분은 같지만 허수 부분의 부호가 반대가 된다.(skew-symmetry)
    • 벡터 V와 W의 내적이 ⟨V∣W⟩=2+3i 라고 가정하였을 때,
    • 벡터 W와 V의 내적 ⟨W∣V⟩=2-3i 가 된다.
    • 두 내적의 결과값은 켤레복소수 관계
  • 벡터 자신과 자신의 내적은 항상 0보다 크거나 같으며, 자기 자신과의 내적이 0이라면 그 벡터는 0벡터이다. |A⟩⋅|A⟩≥0, iff |A⟩=0
    • A벡터의 모든 성분의 제곱 합으로 나타나기 때문!
  • ⟨V|(a|W⟩+b|Z⟩) = a⟨V|W⟩+b⟨V|Z⟩ 가 성립한다.(linearity in ket)
• 내적에서 교환법칙이 성립한다. 즉, 두 벡터의 내적을 계산할 때 순서를 바꿔도 결과는 같다.
• 내적 연산은 선형성(linearity)를 가진다.
  • 즉, |A⟩⋅(b|B⟩ +c|C⟩) = b|A⟩⋅|B⟩ + c|A⟩⋅|C⟩ 성립
• 내적 공간(Inner Product Space) : 내적이 정의된 벡터 공간을 말함.

출처

양자 컴퓨팅 및 정보의 기초_서울대학교 공과대학 김태현 교수님