1. Abstract
- 생성모델의 본질 : 데이터가 존재할법한 분포를 파악해 "실제같은", "실제와 유사한" 데이터를 만드는 것
- 원하는 데이터의 분포를 얼마나 잘 추정했느냐가 생성모델의 Output 품질을 결정
- 본 논문에서는 이 과정에서 두가지 trade-off 관계를 설명하며, Diffusion probabilistic model을 제안함.
- Tractability : Tractable한 모델은 가우시안 분포처럼 수치적으로 계산이 되며 데이터셋이 쉽게 Fit할 수 있지만 이러한 모델은 복잡한 데이터셋을 설명하기 어려움.
- Flexibility : Flexible한 모델은 임의의 데이터에 대해서도 적절하게 설명할 수 있지만, 학습하고 평가하고 샘플을 생성하는데 일반적으로 매우 복잡함.
- Diffusion probabilistic model을 제안함으로서 다음이 가능함을 설명
- 유연한 모델구조 : Forward process과정이 reverse process로 학습만 가능한 형태라면 분포선택에 자유도가 커지므로 보다 유연한 모델구조를 사용할 수 있다
- exact sampling Tractability : 과정이 tractable하기 때문에 정확한 분포값을 사용
- 다른 분포들과의 쉬운 곱셈
- Model log likelihood와 각 state의 확률 계산이 쉽다 : the model log likelihood, and the probability of individual states, to be cheaply evaluated log-likelihood를 직접 계산한다는 장점이 있다. 이는 실제 분포에 대해서 surrogate을 사용하지 않고 Negative log-likelihood를 loss함수에 직접 사용함으로써 목표로하는 분포에 대해 정확한 gradient를 보낼 수 있다는 강력한 장점이 있다
- 여기서 전제되는 성질은 Markov property임.
- 즉 현재상태에서 다음상태로의 변환은 이전상태에 대해 독립적이다. 즉 transition은 이전상태와 무관하게 현재의 독립적인 사건으로 본다는 것이다. Diffusion process에서 중요한 부분은 작은 변화들을 주면서 forward process(noise형태로 만드는 과정)의 역과정을 학습하는 것임.
Algorithm
- diffusion model은 원본 이미지에 gaussian noise를 순차적으로 추가하며 완전한 random noise로 만들어주는 과정(diffusion process)으로부터, 이것의 역변환(inverse process)을 학습하고, 이 학습된 역변환을 사용하여 random noise로부터 이미지를 생성하는 메커니즘을 따른다.
- 주어진 복잡한 데이터분포를 어떤 방식으로 단순하고 tractable한 분포로 바꿀지를 정한 후, 이 과정의 역과정을 학습하면 우리는 단순한 어떤 분포로부터 데이터분포를 만드는 생성모델을 만들 수 있음
- Forward diffusion process
- Data distributon, 즉 실제 데이터의 분포를 라고 하자. 이 데이터 분포는 forward process를 통해 점차 바뀌어 결과적으로 tractable한 로 바뀌게 된다. 이 때 점차 바꾸어가는 과정을 Markov diffusion kernel이라고 하며 이를 에 대한 라고 하며 이 때 는 diffusion rate임.
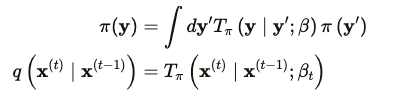
- Data distributon, 즉 실제 데이터의 분포를 라고 하자. 이 데이터 분포는 forward process를 통해 점차 바뀌어 결과적으로 tractable한 로 바뀌게 된다. 이 때 점차 바꾸어가는 과정을 Markov diffusion kernel이라고 하며 이를 에 대한 라고 하며 이 때 는 diffusion rate임.
- Reverse generative process
- Forward diffusion process는 분포를 정하고, 그 분포에 따라 데이터를 변환시키는 과정. 이 과정의 역과정을 추정하는 것이 바로 생성과정이며, reverse generative distribution 이라고 함
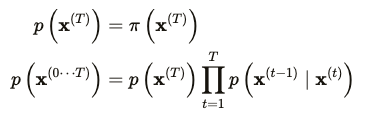
- Diffusion process에서의 계산비용은 위의 reverse diffusion process과정에 대한 학습을 time-step만큼 곱한만큼이 됨.
- Forward diffusion process는 분포를 정하고, 그 분포에 따라 데이터를 변환시키는 과정. 이 과정의 역과정을 추정하는 것이 바로 생성과정이며, reverse generative distribution 이라고 함
- Loss Function
- Reverse diffusion process, 즉 Diffusion 모델을 학습하기 위한 Loss function의 목적은 가우시안 분포 형태로 변환한 Distribution을 추정하는 것이며 이는 주어진 데이터의 likelihood를 계산하는 것으로 판단할 수 있음.
- 따라서 Reverse generative process에서 Loss Function은 log likelihood of x를 계산하는 것이며 수식은 아래와 같음.
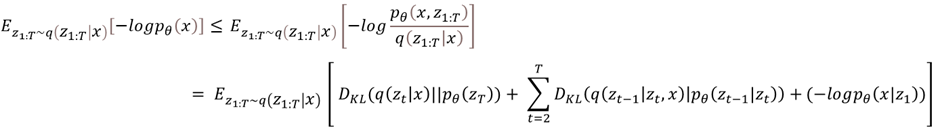
- Forward diffusion process

- 따라서 요약하자면 본 논문에서 제안한 Diffusion 모델의 흐름은 위 그림과 같으며,
- Forward diffusion process : Noise를 점점 증가시켜가면서 학습 데이터를 특정한 가우시안 Noise distribution 으로 변환
- Reverse generative process : noise distribution으로부터 학습 데이터를 복원(denoising)하는 것을 학습. 이 과정을 Markov Chain으로 표현
3. Contributes
- 본 논문의 실험에서는 toy data와 MNIST, CIFAR10, Dead Leaf Images 데이터 셋에 대해서 생성 및 inpainting을 보여주었으며, 각각의 결과물을 볼 때 생성능력 자체가 매우 뛰어나지는 않지만 본 논문에서 언급한 Diffusion process를 기반으로 이러한 생성 작업을 할 수 있다는 가능성을 보여주었다는 것에 큰 의의가 있다고 생각함.
