[알고리즘/C++] 탐색 알고리즘 (Searching Algorithm)

탐색 알고리즘은 여러 요소가 들어있는 자료구조에서 원하는 값을 가져오는 알고리즘을 의미한다. 자료구조의 특성에 따라 효율적인 탐색 알고리즘은 달라진다.

선형 탐색 (Linear Search)

가장 간단하고 직관적인 탐색 알고리즘. 원하는 값을 찾기 위해 리스트나 배열에서 처음부터 순차적으로 탐색하는 방법이다.

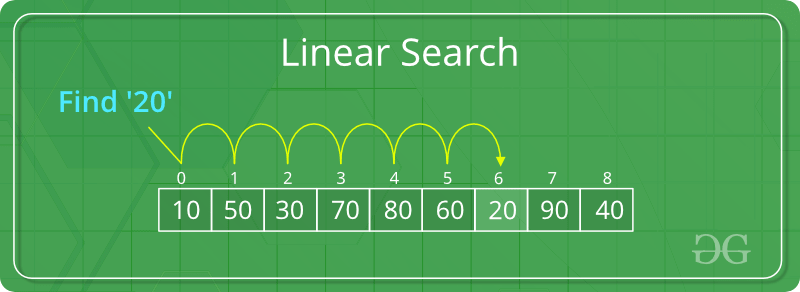
https://www.geeksforgeeks.org/linear-search/?ref=outind

배열의 크기가 크고 탐색해야할 요소가 많은 경우 효율성이 떨어진다.

동작 방식

1. 배열의 첫 번째 요소부터 시작
2. 현재 요소와 찾고자 하는 값과 비교
3. 값이 일치하면 해당 요소의 인덱스 반환
4. 값이 일치하지 않으면 다음 요소로 이동
5. 끝까지 탐색했지만 원하는 값이 없으면 탐색 실패

코드(cpp)

#include <bits/stdc++.h>
using namespace std;

int linearSearch(int* arr, int num, int n) {
    for(int i = 0; i < n; i++) {
        if(arr[i] == num) return i;
    }
}

int main() {
    int arr[10] = {19, 23, 59, 93, 12, 45, 38, 20, 94, 71};
    int n = sizeof(arr) / sizeof(int);
    int num = 12;

    int index = linearSearch(arr, num, n);

    cout << index << endl;
}

linearSearch함수에서 arr을 for문으로 순회하면서 찾고자 하는 값과 같으면 해당 값의 인덱스를 반환한다.

시간복잡도

배열 전체를 비교하므로 시간복잡도는 $O(n)$이다.

---

이진 탐색 (Binary Search)

효율이 떨어지는 선형 탐색 알고리즘을 보완한 빠르고 효율적인 탐색 알고리즘이다. 단, 순회할 배열이나 리스트는 정렬되어 있어야 이진 탐색을 적용할 수 있다.

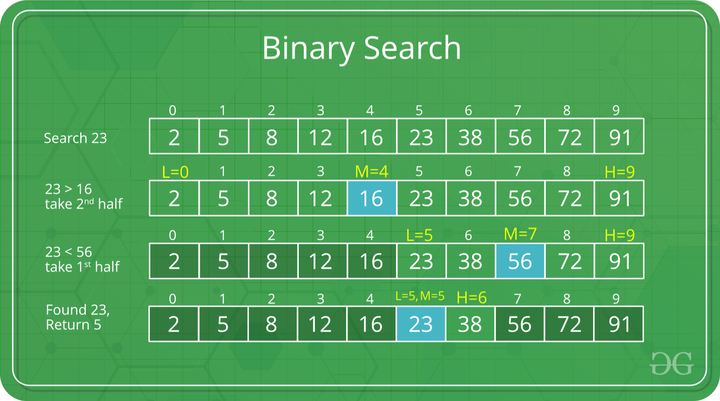
https://www.geeksforgeeks.org/binary-search/?ref=outind

동작방식

1. 배열의 중간 값을 선택
2. 찾고자 하는 값과 중간 값을 비교
3. 일치하면 반환
4. 중간 값보다 작다면, 왼쪽 부분에 대해서 이진 탐색을 재귀적으로 수행
5. 중간 값보다 크다면, 오른쪽 부분에 대해서 이진 탐색을 재귀적으로 수행
6. 찾고자 하는 값을 찾을 때까지 1 ~ 5 과정을 반복

코드(cpp)

#include <bits/stdc++.h>
using namespace std;

int linearSearch(int* arr, int num, int n) {
    for(int i = 0; i < n; i++) {
        if(arr[i] == num) return i;
    }
}

int binarySearch(int*arr, int num, int n) {
    int left = 0;
    int right = n - 1;

    while(left <= right) {
        int mid = (left + right) / 2;

        if(arr[mid] == num) return mid;

        else if(arr[mid] > num) right = mid - 1;

        else if(arr[mid] < num) left = mid + 1;
    }
    return -1;
}

int main() {
    int arr[10] = {12, 19, 20, 23, 38, 45, 59, 71, 93, 94};
    int n = sizeof(arr) / sizeof(int);
    int num = 59;
    
    int index = binarySearch(arr, num, n);

    cout << index << endl;
}

binarySearch함수에서 mid를 설정하고, 타겟값이 arr[mid]과 같으면 반환, 작으면 탐색 영역을 mid 왼쪽으로 옮겨야 하므로 right = mid - 1로 설정한다. 마지막으로 타겟값이 arr[mid]보다 크면 탐색 영역이 mid 오른쪽 이므로 left = mid + 1임을 알 수 있다.

C++의 헤더파일 중 bits/stdc++.h에 binary_search 함수가 존재한다. 필요할 때 번거롭게 구현하지 않고 이를 사용해도 좋다고 생각한다.

시간복잡도

이진 탐색은 매 단계마다 탐색 범위를 중간 값을 기준으로 반으로 줄이기 때문에 시간복잡도는 $O(log_2n)$이다. 대규모 데이터에서 순차 탐색과 비교하였을 때 강력한 효율을 보이지만, 정렬된 데이터에서만 유효하다.

---

해시 탐색 (Hash Search)

해시 함수를 이용해 다양한 크기의 데이터를 고정된 크기의 값인 해시 값을 인덱스로 사용하여 배열 혹은 해시 테이블에 저장한다.

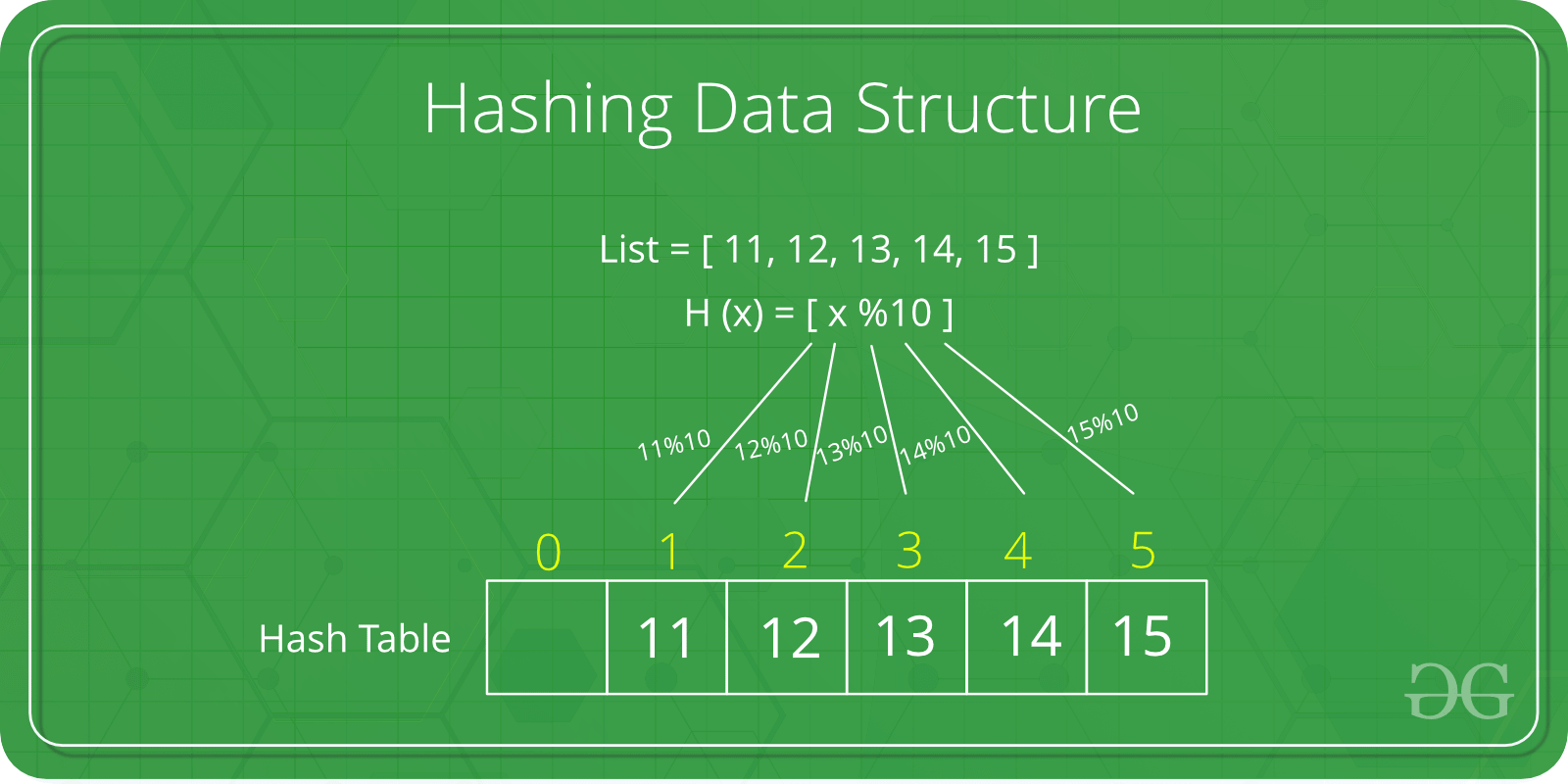
https://www.geeksforgeeks.org/hashing-data-structure/?ref=shm

위의 예시로, $H(x) = [\text{x mod 10}]$인 해시 함수는 x값에 어떤 수가 들어가도 0에서 9까지의 수를 반환한다. 이를 인덱스로 활용하여 0에서 9까지의 인덱스를 가진 해시 테이블에 저장한다.

만약 x = 25, 35이게 되면 해시 값은 모두 5로 똑같아서 한 인덱스에 두 개의 값이 들어가야하는 충돌이 발생하는 경우가 생긴다. 이를 해결하기 위한 방법으로는 연결리스트를 사용하여 중복된 값들을 연결하거나, 다른 위치에 저장하는 방법이 존재한다.

즉, 다양한 값에 대해 한쪽으로 해시 값을 몰리게 도출하지 않고 모든 해시 값에 대해 골고루 도출하는 해시함수가 데이터를 분산시키고 충돌을 최소화하는 좋은 해시함수이다.

동작방식

1. 저장할 값을 해시함수에 넣어 인덱스를 반환
2. 반환된 인덱스 위치가 빈 공간이라면 해당 공간에 값 초기화
3. 이미 값이 들어있다면, 연결리스트를 활용하거나, 옆의 빈 공간으로 값을 삽입

시간복잡도

해시 함수를 사용하여 데이터를 저장하기 때문에 검색 속도가 매우 빠르다. 일반적으로 상수 시간의 시간복잡도를 가진다. ($O(1)$)

---