[알고리즘/C++] 정렬 알고리즘 (Sorting Algorithm)

임원재·2024년 4월 28일
algorithmcpp
0

Algorithm

목록 보기
1/7

정렬 알고리즘은 배열을 특정한 순서로 재배열하는 알고리즘이다. 매우 다양한 분야에서 사용되며 다양한 종류의 정렬 알고리즘이 존재한다. 데이터, 즉 배열의 특징과 요구되는 시간복잡도에 따라 각각 다른 알고리즘이 사용된다.

Selection Sort (선택 정렬)

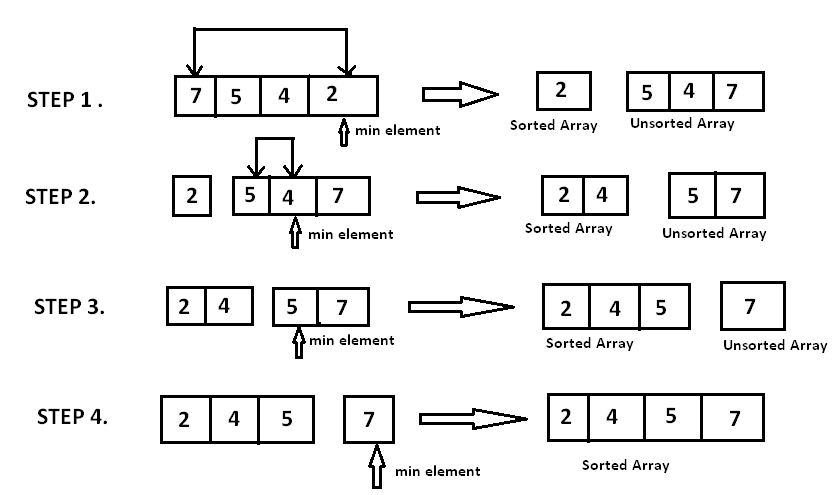
간단하고 효과적인 정렬 알고리즘, 추가적인 메모리를 요구하지 않는 정렬 방법

출처 : https://www.hackerearth.com/practice/algorithms/sorting/selection-sort/tutorial/

배열 중 정렬되지 않은 부분에서 가장 작은 값 (혹은 가장 큰 값)을 선택(Selection)하여 해당 정렬되지 않은 부분 중 가장 첫 요소와 교환하는 방식이다. 배열 전체의 요소가 정렬될 때까지 남은 정렬되지 않은 배열에 대해 해당 방식을 반복한다.

#include <bits/stdc++.h>
using namespace std;

void swap(int *arr, int a, int b) {
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
}

void selectionSort(int* arr, int n) {
    
    int min;
    for(int i = 0; i < n; i++) {
        min = i;

        for(int j = i + 1; j < n; j++) {
            min = arr[min] > arr[j] ? j : min;
        }

        if(i != min) swap(arr, i, min);
    }
}

int main() {
    int arr[] = {4, 7, 2, 6, 9, 1};
    int n = sizeof(arr) / sizeof(int);

    selectionSort(arr, n);

    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
}

해당 코드로 오름차열 배열을 정렬하였다. 배열중 가장 작은 요소를 찾는 반복 횟수를 i-for문에서 정의하였다. 이때의, i는 곧 찾을 최소 요소와 자리를 바꿀 요소의 인덱스가 된다. j-for문에서 순회하는 배열에서 가장 작은 요소의 인덱스 min을 찾는다.

이때, j-for문에서 찾은 min과 i가 같다면, 이는 해당 자리에 정렬되지 않은 최솟값이 이미 올바르게 들어가있음을 알 수 있다.

즉, i와 min이 다를 때만 두 요소의 값을 swap하면 된다.

시간복잡도

한 요소에 대해 전체를 순회하여 최솟값을 판단하므로 O(n2)O(n^2)이다.

Insertion Sort (삽입 정렬)

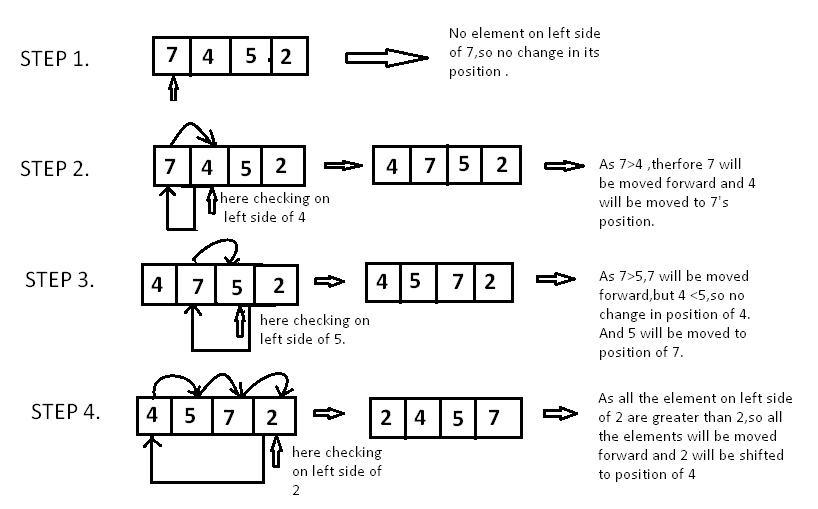
간단한 알고리즘, 정렬되지 않은 배열 부분에서의 각각의 요소를 정렬된 배열의 부분에 삽입하는 방식이다. 추가적인 메모리를 필요로 하지 않는다.

출처 : https://www.hackerearth.com/practice/algorithms/sorting/insertion-sort/tutorial/

선택정렬과 비슷한 순회를 보이지만, 순회를 돌며 정렬된 배열부분에 중간, 끝, 또는 시작지점에 삽입(Insertion)한다는 점에서 차이를 보인다. 해당 알고리즘의 코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

void swap(int *arr, int a, int b) {
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
}

void insertionSort(int* arr, int n) {
    
    int key, j;
    for(int i = 1; i < n; i++) {
        key = arr[i];
        
        j = i - 1;
        while(j >= 0 && arr[j] > key) {
            arr[j+1] = arr[j];
            j--;
        }
        
        arr[j+1] = key;
    }
}

int main() {
    int arr[] = {4, 7, 2, 6, 9, 1};
    int n = sizeof(arr) / sizeof(int);

    insertionSort(arr, n);

    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
}

먼저, 0-for문에서 0번째 인덱스는 정렬되어 있다는 가정 하에 i = 1에서부터 순회를 시작한다. i번째 인덱스값을 정렬할 요소(key)로 선택된다. 0 ≤ j ≤ i - 1의 범위인 정렬된 배열 부분에 대해 arr[j]이 key값보다 크다면, key는 arr[j]보다 앞으로 와야 정렬이 되기 때문에 arr[j+1] = arr[j]로 arr[j]을 뒤로 한칸 미룰 수 있다. 이를 반복하여 key가 올 알맞은 인덱스 j+1값이 정해졌다면, arr[j+1] = key로 정렬 가능하고, 이를 1 ≤ i < n 반복하면 정렬이 완료된다.

시간복잡도

한 요소에 대해 전체를 순회하여 삽입될 자리를 찾으므로 O(n2)O(n^2)이다.

만약 이미 정렬된 배열에 대해 삽입 정렬을 진행하면 한 요소에 대해 진행할 순회가 없으므로 O(n)O(n)이다.

Bubble Sort (버블정렬)

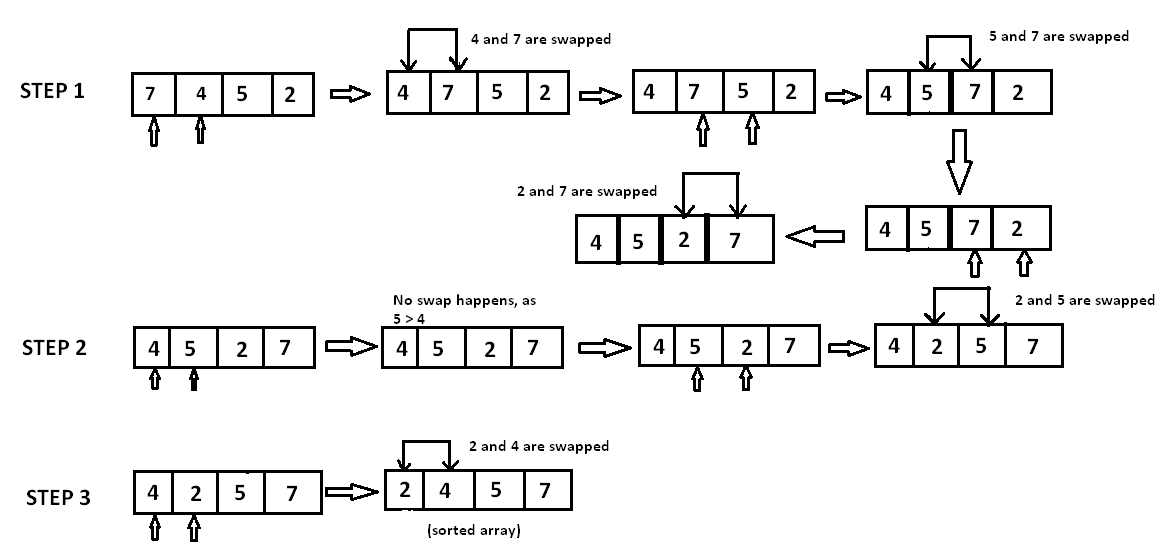
인접한 요소에 대해 정렬이 되어있지 않으면 swap을 반복적으로 진행하는 알고리즘. 추가적인 메모리를 필요로 하지 않는다. 정렬이 거품처럼 발생하기에 버블정렬이라고 부르는듯하다.

출처 : https://www.hackerearth.com/practice/algorithms/sorting/bubble-sort/tutorial/

#include <bits/stdc++.h>
#include <time.h>
using namespace std;

void swap(int *arr, int a, int b) {
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
}

void bubbleSort(int* arr, int n) {
    
    int key, j;
    for(int i = 0; i < n - 1; i++) {
        for(int j = 0; j < n - i - 1; j++) {
            if(arr[j] > arr[j+1]) swap(arr, j, j + 1);
        }
    }
}

int main() {
    int arr[] = {4, 7, 2, 6, 9, 1};
    int n = sizeof(arr) / sizeof(int);

    bubbleSort(arr, n);

    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
}

단순히 배열의 한 요소에 대해 전체 순회를 돌며 arr[j] > arr[j+1]이면 서로를 swap한다. 결국엔 각 순회가 끝날 때마다 맨 오른쪽에는 정렬된 요소가 오름차순으로 순차적으로 쌓이게 된다.

시간복잡도

n에 대하여 중첩으로 for문을 실행하기 때문에 O(n2)O(n^2)이다.

Merge Sort (합병정렬)

분할정복을 사용하는 정렬 알고리즘. 정렬할 배열만큼의 메모리 공간을 추가로 요하는 방법이다. 분할정정복은 주어진 문제를 동일한 위상의 작은 문제로 나누고, 이를 해결하는 방식이다. 이를 사용하여 정렬할 배열을 나누고, 이를 합칠 때 정렬을 진행하게 된다.

출처 : https://www.hackerearth.com/practice/algorithms/sorting/merge-sort/tutorial/

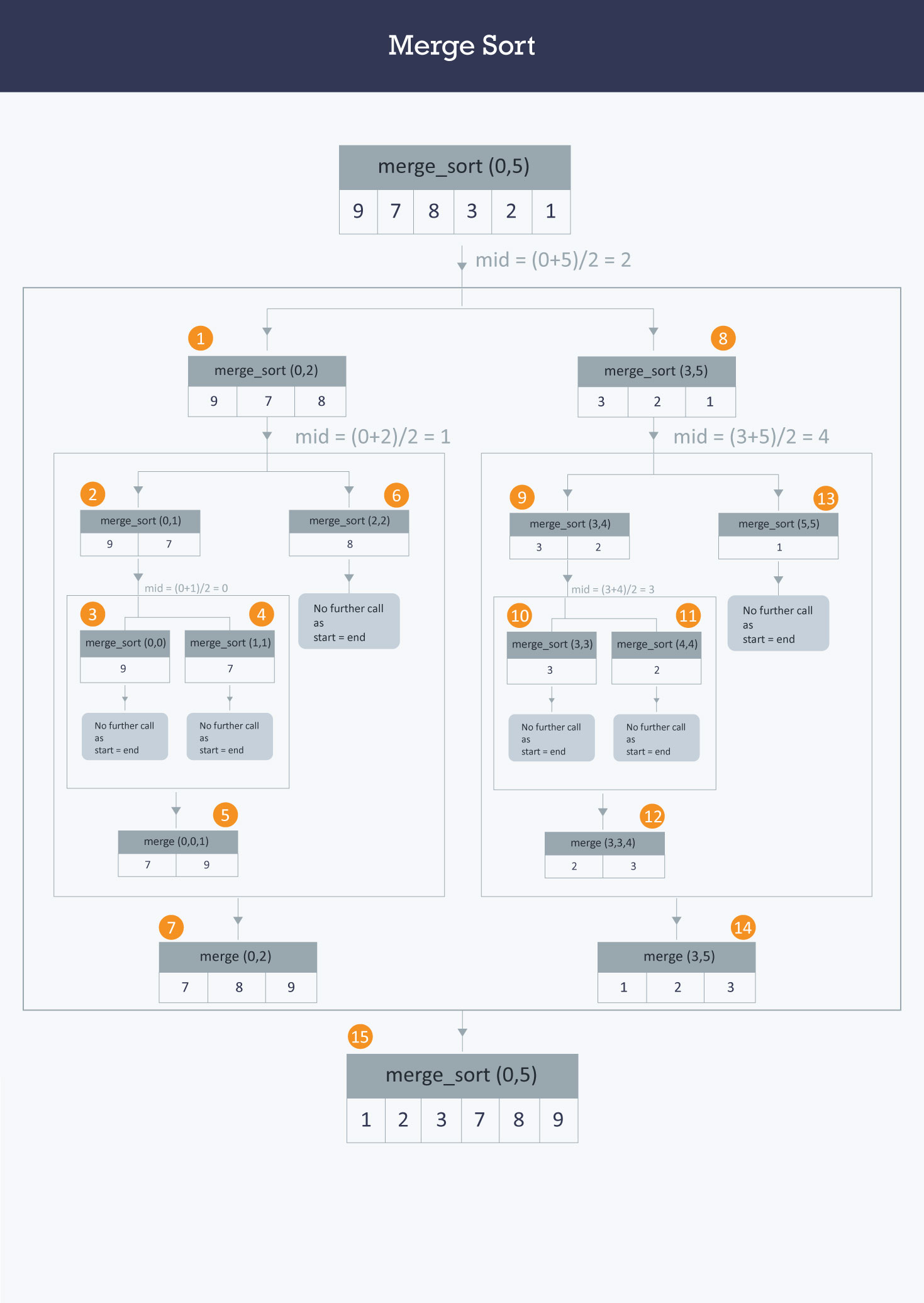
합병정렬을 이해하는데 있어 중요한 것은 배열을 쪼개기 위한 재귀와, 이를 정렬에 맞게 병합하는 머지함수에 대한 이해라고 생각한다.

위 사진을 참고하였을 때, 1~4, 8~11단계가 주어진 배열을 절반으로 나눠 결국엔 하나의 요소밖에 남지 않도록 한다. 이를 분할정복 알고리즘 측면으로 해석했을 때, 주어진 문제를 동일한 위상의 작은 문제로 나눈 부분이라고 볼 수 있다.

5, 7, 12, 14, 15단계에서 하나씩 나눠진 요소를 합치는 과정에서 정렬을 진행하게 된다.

아래 합병정렬을 구현하였다.

#include <bits/stdc++.h>
using namespace std;

int sorted[6];

void merge(int *arr, int left, int mid, int right) {
    int i = left;
    int j = mid + 1;
    int idx = left;

    //arr -> sorted로의 합병
    while(i <= mid && j <= right) {
        if(arr[i] <= arr[j]) {
            sorted[idx++] = arr[i++];
        }
        else {
            sorted[idx++] = arr[j++];
        }
    }

    // 남은 arr값 sorted로 이동
    while (i <= mid) {
        sorted[idx++] = arr[i++];
    }
    // 남은 arr값 sorted로 이동
    while (j <= right) {
        sorted[idx++] = arr[j++];
    }

    // 재사용위해 sorted된 값들을 arr로 복사
    for(int k = left; k <= right; k++) {
        arr[k] = sorted[k];
    }
}

void mergeSort(int* arr, int start, int end) {
    int mid;
    if(start < end) {
        mid = (start + end) / 2;
        mergeSort(arr, start, mid);
        mergeSort(arr, mid+1, end);
        merge(arr, start, mid, end);
    }
}

int main() {
    int arr[] = {4, 7, 2, 6, 9, 1};
    int n = sizeof(arr) / sizeof(int);

    mergeSort(arr, 0, n-1);

    for (int i = 0; i < n; i++)
    {
        cout << sorted[i] << " ";
    }
}

mergeSort 함수에서, 배열의 시작, 끝 인덱스를 파라미터로 받고 이를 절반으로 나눠 다시 mergeSort함수를 호출하였다. 해당 과정이 배열을 작은 문제로 나누는 과정이다.

if 조건문인 start < end를 만족하지 않는 것은 요소가 하나 이하라는 것이므로 mergeSort의 재귀과정이 끝나면 merge함수가 실행된다.

이때 나눈 두 배열을 하나로 합치는 과정에서 전체 배열과 같은 크기의 보조 배열을 사용한다. 각각의 두 배열이 요소를 하나 가지고 있을 때부터 정렬하여 하나의 배열로 합쳐지면, 연쇄적으로 두 배열이 한 배열로 합쳐지면서 정렬됨을 확인할 수 있다.

시간복잡도

전체 배열을 이등분하는 과정에 전체를 순회하여 한 배열로 합치므로 시간복잡도는 O(nlog2n)O(n log_2{n})이다.

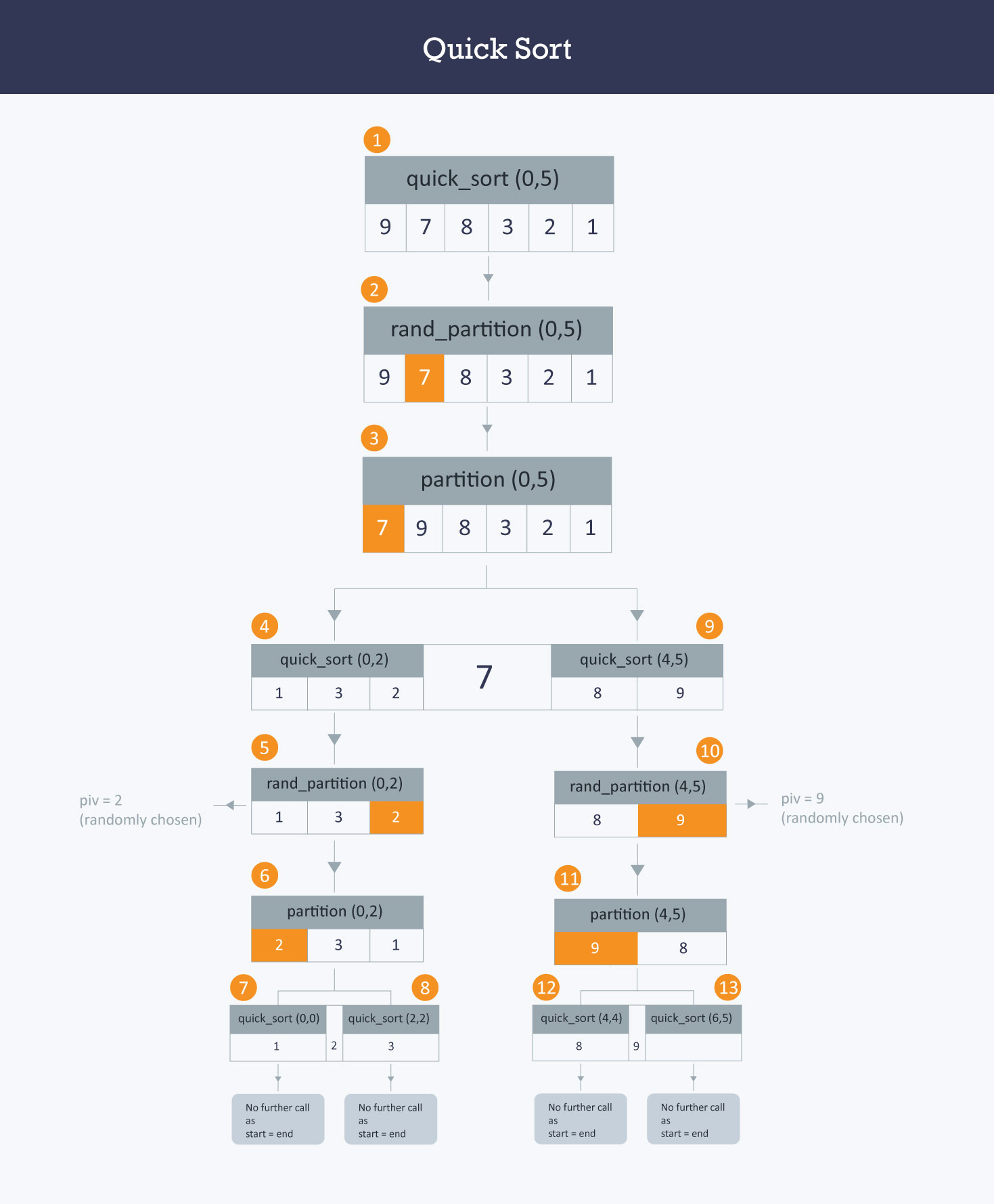
Quick Sort (퀵정렬)

분할정복 알고리즘을 기반으로 하는 정렬 알고리즘이라는 점에서 합병정렬과 비슷한 성질을 가진다. 합병정렬을 두 배열을 합쳐 정렬하는 방식을 취했고, 퀵정렬을 기준(pivot)을 잡고 각 요소와 기준과의 대소비교를 통해 배열을 두 부분으로 나누는 방식을 가진다.

또한 퀵정렬은 추가적인 메모리를 요하지 않는다는 점에서 합병정렬과의 차이점을 보인다.

출처 : https://www.hackerearth.com/practice/algorithms/sorting/quick-sort/tutorial/

#include <bits/stdc++.h>
using namespace std;

void swap(int *arr, int a, int b) {
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
}

int partition(int *arr, int left, int right) {
    int low = left + 1;
    int high = right;

    int pivot = arr[left];

    while(low < high) {
        while(low <= right && arr[low] < pivot) low++;
        while(high >= left && arr[high] > pivot) high--;

        if(low <= high) {
            swap(arr, low, high);
        }
    }

    swap(arr, left, high);

    return high;
}

void quickSort(int* arr, int start, int end) {
    if(start < end) {
        int pivot = partition(arr, start, end);
        quickSort(arr, start, pivot-1);
        quickSort(arr, pivot+1, end);
    }
}

int main() {
    int arr[] = {4, 7, 2, 6, 9, 1};
    int n = sizeof(arr) / sizeof(int);

    quickSort(arr, 0, n-1);

    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
}

quickSort 함수에서, partition 함수를 호출한다. partition함수에서는 주어진 배열을 가지고 pivot값을 정하고 해당 값을 기준으로 왼쪽에는 작은 수, 오른쪽에는 큰 수가 오도록 배열을 swap한다. partition함수 호출이 완료되면, 그 후 pivot기준으로 왼쪽 배열의 quickSort, pivot기준으로 오른쪽 배열의 quickSort 총 2번의 재귀적으로 호출되는 quickSort를 통해 pivot으로 나눈 배열을 정렬하게 된다.

시간복잡도

pivot을 설정하고 나눌때 평균적으로 이등분을 하게 되며, pivot기준으로 배열을 정렬하게 되므로 한번의 단계에서 전체 순회가 발생하게 된다. 즉, 시간복잡도는 O(nlog2n)O(nlog_2n)이다.

만약 pivot을 설정하고 나눌때 이등분이 되지 않고 극단적으로 한개 혹은 나머지로 나눠진다면 시간복잡도는 커진다. 모든 나누는 과정이 하나 혹은 그 나머지로 나눠진다면, 최악의 시간복잡도는 O(n2)O(n^2)이다.

Radix Sort (기수 정렬)

기수별로 정렬을 진행하는 선형적 정렬 알고리즘이다. 이는 자릴수가 정해진 정수나 문자열을 정렬할 때 효과적인 알고리즘이다. 추가적인 메모리 공간을 필요로 한다. 요소간의 비교연산을 진행하지 않는다는 점이 특징이다.

0부터 9까지의 큐에 일의 자릿수부터 대응되는 큐에 push한다. 가장 작은 인덱스의 큐부터 pop()을 하여 다시 배열을 재배치한 뒤, 점층적으로 큰 자릿수에 대응되는 큐의 인덱스에 push한다. 이를 배열의 요소의 최대 자릿수까지 반복하여 원래 배열에 배치하면 정렬이 완료된다.

#include <iostream>
#include <queue>
using namespace std;

queue<int> q[10];

int getDigits(int num, int digit) {
    while(digit) {
        num /= 10;
        digit--;
    }
    return num;
}

void radixSort(int* arr, int n) {
    int digits = 2;
    for(int i = 0; i < digits; i++) {

        for(int j = 0; j < n; j++) {
            int num = getDigits(arr[j], i);
            q[num].push(arr[j]);
        }

        int idx = 0;
        for(int j = 0; j < 10; j++) {

            while(!q[j].empty()) {
                arr[idx] = q[j].back();
                q[j].pop();
                idx++;
            }
        }
    }
}

int main() {
    int arr[] = {41, 74, 23, 61, 98, 13};
    int n = sizeof(arr) / sizeof(int);

    radixSort(arr, n);

    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << " ";
    }
}

요소 모두 2자릿수라고 가정하에 코드를 작성하였다. 큐를 10개를 가진 배열을 생성한 뒤, getDigit 함수를 사용하여 배열에서 각 첫번재 자리수를 확인하고 해당 큐의 해당 인덱스에 push한다. 그 후, 큐에서 순서대로 배열에 pop()을 하여 배열을 재배치한다. 이를 최대 자릿수인 2번 반복하면 정렬되는 것을 확인할 수 있다.

시간복잡도

기수 정렬의 시간복잡도는 최대 자릿수(m) x (n + 10)이므로 빅오표기법에 의해 O(n)O(n)를 갖는다.

profile
임원재
다음 포스트

[알고리즘/C++] 탐색 알고리즘 (Searching Algorithm)

0개의 댓글