[백준/C++] 10830 행렬 제곱

문제

문제 링크 : 10830

크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.

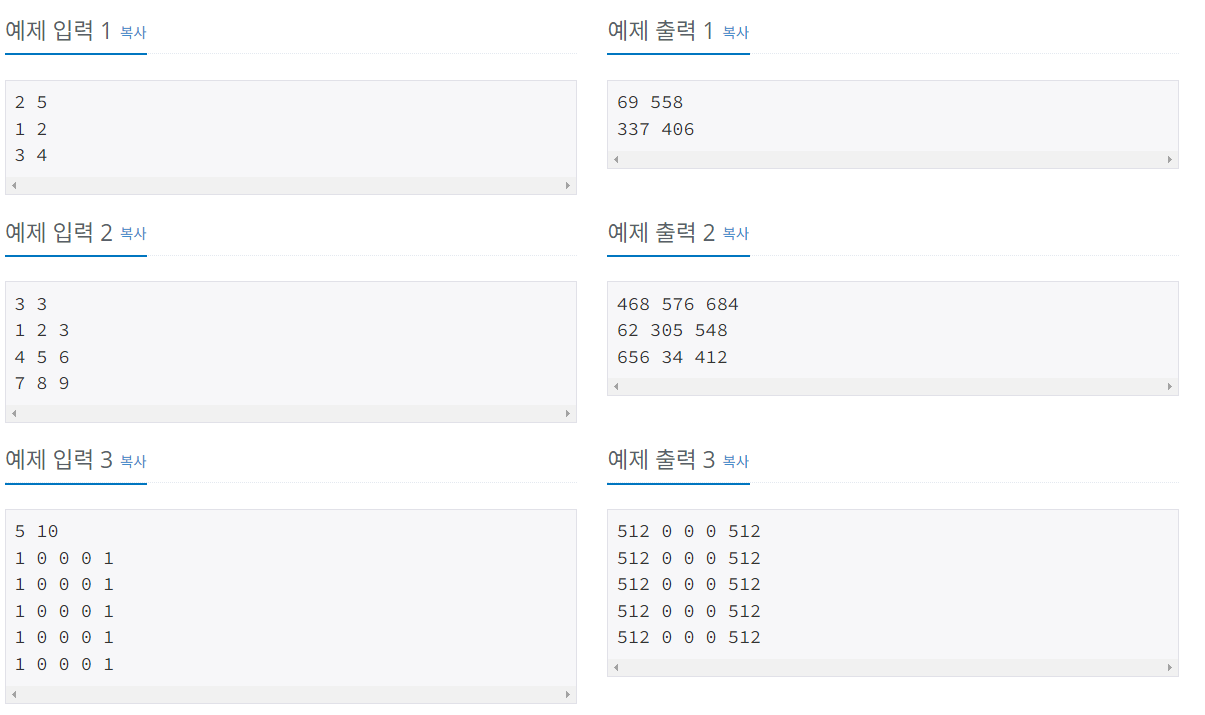
입력

첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.

출력

첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.

---

접근법

행렬의 제곱을 구하는 문제이다. $B$의 범위가 <= 100,000,000,000이므로 해당 변수는 long long으로 받아야 한다. 또한 제곱 과정에서 오버플로가 날 것을 대비하여 1000으로 나눈 나머지를 사용하는 모듈러 연산의 성질이 필요함을 유추할 수 있다.
해당 성질은 다음과 같다.

$(A \times B) \div C = ((A \div C) \times (B \div C)) \div C$

$A$와 $B$가 이미 큰 수여서 $A$와 $B$를 곱하여 오버플로우가 날 가능성이 있다. 이를 막기 위해 먼저 $A$와 $B$를 각각 $C$로 나누어 이를 곱하고, 다시 $C$로 나눈다는 아이디어가 있다. 다음과 같은 연산도 위의 모듈러 연산의 성질에 의해 다르지 않음을 확인할 수 있다.

---

제곱은 지수만큼 곱하기보다 제곱하는 방향으로 진행하면 $O(n)$의 시간복잡도를 $O(logn)$까지 줄일 수 있다.

예를 들어, 기존의 방식으로는 $A^8$을 구하기 위해서 $A$를 7번 곱하는 $O(n)$의 시간복잡도의 방식을 사용한다.

$O(logn)$의 방식은 제곱한 수를 다시 제곱하는 방식이다. $A^8$은 $(((A^2)^2)^2)$으로 총 3번의 연산을 수행한다. ($log8 = 3$)

홀수일 때는 $A^{2n+1}=(A^n)(A^n)(A)$와 같이 표현 가능하다.

예시를 들어 $A^{10} = (((A^2)^2)^2 \times A^2) = (A^8 \times A^2)$와 같이 표현할 수 있는 것이다.

구현 코드는 아래와 같다.

---

코드

#include <bits/stdc++.h>
#define MAX 6
using namespace std;

long long mul[MAX][MAX];
long long matrix[MAX][MAX];
long long n, b;

void multiply(long long a1[MAX][MAX], long long a2[MAX][MAX]) {
    long long copy[MAX][MAX];
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            copy[i][j] = 0;
            for(int k = 0; k < n; k++) copy[i][j] += a1[i][k] * a2[k][j];
            copy[i][j] %= 1000;
        }
    }

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            a1[i][j] = copy[i][j];
        }
    }
}

int main() {
    cin >> n >> b;

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> mul[i][j];
        }
        matrix[i][i] = 1;
    }

    while(b > 0) {
        if(b % 2 == 1) {
            multiply(matrix, mul);
            b -= 1;
        }
        else {
            multiply(mul, mul);
            b /= 2;
        }
    }

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cout << matrix[i][j] << " ";
        }
        cout << '\n';
    }
}

multiply함수에서는 파라미터로 배열을 받아 이를 곱한다. 곱한것을 copy배열에 임시저장해놓은 뒤, for문으로 a1배열의 파라미터에 넣는다.

---

    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> mul[i][j];
        }
        matrix[i][i] = 1;
    }

해당 부분은 mul이라는 배열에 곱할 값을 입력받는 부분이다. matrix는 mul행렬을 제곱하여 결과값으로 사용할 목적이다.

즉, 처음 matrix x mul을 진행할 때 1 x 5 = 5인 것처럼 matrix x mul = mul이 되어야 한다. 만약 matrix가 모두 0으로 초기화된다면 이는 스칼라로써는 0과 같은 의미이다. 0 x 5 = 0과 같이 곱셈이 불가하다.

이를 해결하려면 matrix를 스칼라에서 1에 대응하는 특정한 행렬로 바꾸어야 한다. 이를 단위행렬(I)이라고 한다. 단위행렬은 주대각선의 원소가 1이고 나머지가 0인 행렬이다. 단위행렬에 어떠한 행렬을 곱해도 동일한 행렬이 나오므로 스칼라에서 1에 대응한다고 볼 수 있다$(I \times A = A)$. 그러므로 matrix를 단위행렬로 matrix[i][i] = 1과 같이 초기화 해주어야 한다.

---

    while(b > 0) {
        if(b % 2 == 1) {
            multiply(matrix, mul);
            b -= 1;
        }
        else {
            multiply(mul, mul);
            b /= 2;
        }
    }

해당 구현에서 가장 중요한 부분이라고 생각한다.
$b$가 5라고 가정해보자, $b$가 홀수이므로 multiply(matrix, mul)을 실행한다. 위에서 언급했듯이 matrix와 mul을 곱해 결과를 matrix에 저장한다. 이때 matrix는 제곱의 결과를 출력할 배열이고, mul은 곱할 행렬(A)을 뜻한다. matrix = $(A)$. 홀수일 때 mul을 곱했으므로 $b$에서 1을 뺀다$(b = 4)$.

$b$가 짝수가 되었으므로 multiply(mul, mul)을 호출하여 mul을 제곱한다 $(=A^2)$. 후에 $b$를 2로 나눈다 ($b$ = 2).

다시 $b$가 짝수가 되었으므로 multiply(mul, mul)을 호출하여 mul이 $(=A^4)$로 제곱된다. 후 $b$는 1이 된다.

if(b % 2 == 1)에 걸려 matrix와 mul을 곱한다. 이때 mul은 $(=A^4)$가 되었으므로 matrix x mul은 $(A \times A^4 = A^5)$가 된다. 후 b -= 1를 진행해 $b$ = 0이 되어 while문에서 나간다.($b$는 int형)

---

느낀점

아무리 큰 제곱수더라도 위와 같은 방식으로 $O(logn)$의 방식으로 구현 가능함을 알게 되었다. 작은 제곱수부터 곱해 나가는 것이 분할정복과 비슷하다고 느껴졌다. 앞으로도 비슷한 문제가 나왔을 때 위와 같은 사고를 할 수 있도록 좀 더 노력해야겠다고 생각했다.

기계학습을 배우면서 행렬을 다룰 일이 많았는데 백준에서 행렬을 푸는건 처음이었던 것 같았다. 행렬에도 다양한 연산이 있고 해당 연산을 줄여주는 행렬과 관련된 알고리즘이 있다. 이에 더 많이 공부해야겠다고 생각한다.