문제
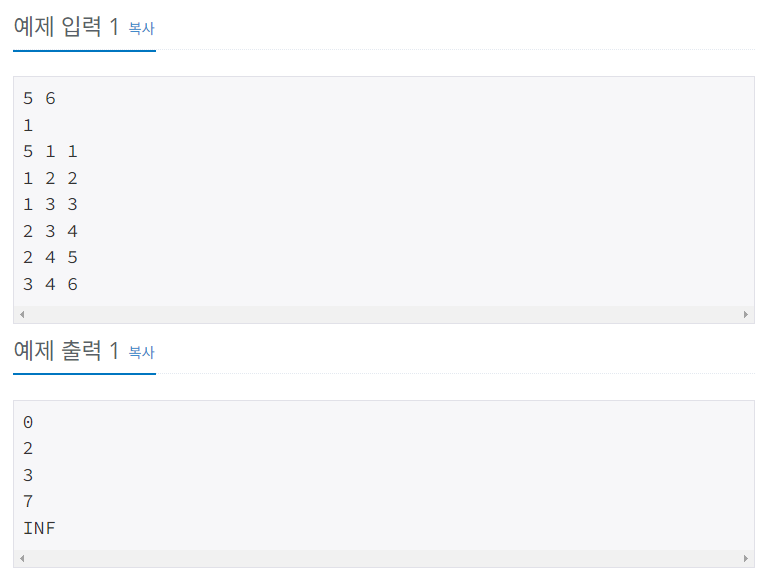
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
출력
첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.
접근법
전형적인 다익스트라 알고리즘을 사용하는 문제이다. 잘 구현해서 제출했는데 잘 가다가 시간초과가 발생하였다. 우선순위 큐를 사용해서 시간복잡도 관리도 잘 하였고 예시 입출력도 동일하였고 이것저것 반례도 고려하였기에 문제를 찾지 못하였다.
입력받고 출력하는데 시간을 많이 잡아먹나 생각하여
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);과 같은 코드를 삽입하여도 결과는 시간초과였다. 2시간정도 코드를 뜯어보고 삽질해본 결과, 우서순위 큐에서 실수를 하였다.
우선순위 큐를 선언할 때
priroriy_queue<pair<int, int>> pq;와 같이 선언하였다. 이때 first부분을 노드번호, second부분을 거리로 사용했던 것이 문제였었다. 우선순위 큐는 큐에 들어오는 순서와 상관없이 가장 큰 값이 top을 향하도록 하는 자료구조이다. 즉, max heap을 사용하여 우선순위 큐를 구현하게 된다.
위 문제와 같은 상황에서 자료형을 pair<int, int>로 선언하였기에 first부분에 해당하는 값을 기준으로 max heap이 계산되었을 것이다.
다익스트라 알고리즘에서 우선순위 큐의 사용 목적은 노드중에서 가장 거리가 짧은 노드를 먼저 꺼낼 수 있도록 하는 것이다. 하지만 노드번호를 first부분으로 두어 거리와는 무관하게 작은 노드번호먼저 pop()되는 무의미한 계산이 있었기에 시간초과가 날 수 밖에 없었다.
int cur_node = pq.top().second;
int cur_dist = -pq.top().first;이를 인지하고 거리가 짧은 노드가 먼저 pop()되도록 수정하였다. 오름차순 정렬이므로 삽입하려는 값에 음수(-)처리를 하여 max heap을 min heap으로 바꿔주는 과정도 필요하다. 위 코드처럼 pair에서 first부분이 힙으로 push되도록 하였다.
전체코드는 아래와 같다.
코드
#include <iostream>
#include <vector>
#include <queue>
#define MAX 300001
#define INF 1000000
using namespace std;
// <노드번호, 거리> -> <거리, 노드번호>
priority_queue<pair<int, int>> pq;
vector<pair<int, int>> graph[MAX];
int dist[20001];
int V, E, K;
void dijkstra(int start) {
pq.push({0, start});
dist[start] = 0;
while(!pq.empty()) {
int cur_node = pq.top().second;
int cur_dist = -pq.top().first;
pq.pop();
if(dist[cur_node] < cur_dist) continue;
for(int i = 0; i < graph[cur_node].size(); i++) {
int nxt_node = graph[cur_node][i].first;
int nxt_dist = graph[cur_node][i].second + cur_dist;
if(dist[nxt_node] > nxt_dist) {
dist[nxt_node] = nxt_dist;
pq.push({-nxt_dist, nxt_node});
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
scanf("%d %d", &V, &E);
scanf("%d", &K);
int u, v, w;
for(int i = 0; i < E; i++) {
scanf("%d %d %d", &u, &v, &w);
graph[u].push_back({v, w});
}
for(int i = 0; i <= V; i++) {
dist[i] = INF;
}
dijkstra(K);
for(int i = 1; i <= V; i++) {
if(dist[i] == INF)
printf("INF\n");
else
printf("%d\n", dist[i]);
}
return 0;
}느낀점
실수를 하지 않았다고 확신을 하였기에 애먼 곳을 자꾸 수정하였다. 내가 짠 코드가 맞다고 대충 훑어보지 않고 충분히 틀릴 수 있음을 명심하고 찬찬히 훑어보는 연습이 필요함을 깨달았다. 빠르고 완벽하게 짜는 연습보다, 틀린 곳을 진득하게 찾아볼 수 있는 태도를 길러야겠다.