[백준/C++] 2630 색종이 만들기

문제

아래 <그림 1>과 같이 여러개의 정사각형칸들로 이루어진 정사각형 모양의 종이가 주어져 있고, 각 정사각형들은 하얀색으로 칠해져 있거나 파란색으로 칠해져 있다. 주어진 종이를 일정한 규칙에 따라 잘라서 다양한 크기를 가진 정사각형 모양의 하얀색 또는 파란색 색종이를 만들려고 한다.

전체 종이의 크기가 N×N(N=2k, k는 1 이상 7 이하의 자연수) 이라면 종이를 자르는 규칙은 다음과 같다.

전체 종이가 모두 같은 색으로 칠해져 있지 않으면 가로와 세로로 중간 부분을 잘라서 <그림 2>의 I, II, III, IV와 같이 똑같은 크기의 네 개의 $\frac{N}{2}$ × $\frac{N}{2}$ 색종이로 나눈다. 나누어진 종이 I, II, III, IV 각각에 대해서도 앞에서와 마찬가지로 모두 같은 색으로 칠해져 있지 않으면 같은 방법으로 똑같은 크기의 네 개의 색종이로 나눈다. 이와 같은 과정을 잘라진 종이가 모두 하얀색 또는 모두 파란색으로 칠해져 있거나, 하나의 정사각형 칸이 되어 더 이상 자를 수 없을 때까지 반복한다.

위와 같은 규칙에 따라 잘랐을 때 <그림 3>은 <그림 1>의 종이를 처음 나눈 후의 상태를, <그림 4>는 두 번째 나눈 후의 상태를, <그림 5>는 최종적으로 만들어진 다양한 크기의 9장의 하얀색 색종이와 7장의 파란색 색종이를 보여주고 있다.

입력으로 주어진 종이의 한 변의 길이 N과 각 정사각형칸의 색(하얀색 또는 파란색)이 주어질 때 잘라진 하얀색 색종이와 파란색 색종이의 개수를 구하는 프로그램을 작성하시오.

입력

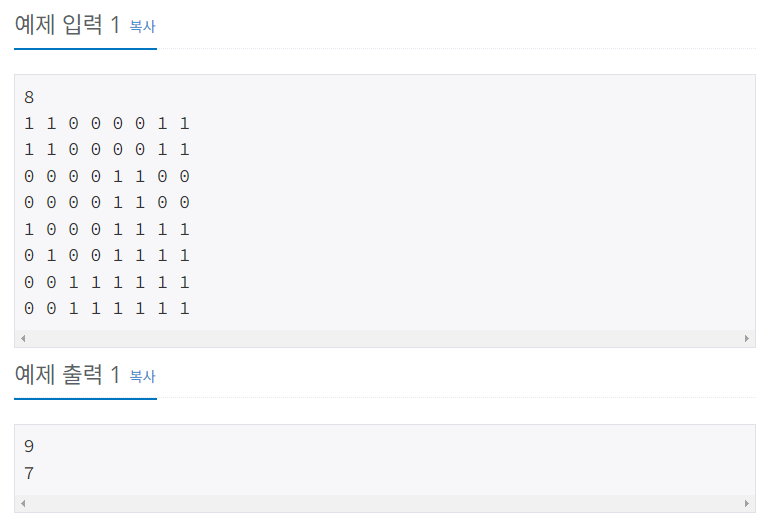
첫째 줄에는 전체 종이의 한 변의 길이 N이 주어져 있다. N은 2, 4, 8, 16, 32, 64, 128 중 하나이다. 색종이의 각 가로줄의 정사각형칸들의 색이 윗줄부터 차례로 둘째 줄부터 마지막 줄까지 주어진다. 하얀색으로 칠해진 칸은 0, 파란색으로 칠해진 칸은 1로 주어지며, 각 숫자 사이에는 빈칸이 하나씩 있다.

출력

각 테스트 케이스에 대해 문서가 몇 번째로 인쇄되는지 출력한다.

---

접근법

문제의 상황은 다음과 같다. 종이의 크기가 1보다 크게 되면 이를 정사각형으로 4등분하여 똑같은 상황을 가정하게 된다. 즉, 가로 세로의 길이가 8일때 8 -> 4 -> 2 -> 1로 작은 문제로 분할하여 크기가 1이 돼서야 연산을 진행하게 되는 전형적인 분할정복 방식이다.

이에 분할정복을 재귀함수로 구현하게 되었다. 밑에 cpp로 구현한 코드가 있다.

---

코드

#include <iostream>
#define MAX 128
#define WHITE 0
#define BLUE 1
using namespace std;
int white = 0;
int blue = 0;

int N;

int arr[MAX][MAX];

void divide(int row_start, int row_end, int col_start, int col_end) {
    int w_cnt = 0;
    int b_cnt = 0;

    for(int i = row_start; i <= row_end; i++) {
        for(int j = col_start; j <= col_end; j++) {
            if(arr[i][j] == WHITE) w_cnt++;
            else if(arr[i][j] == BLUE) b_cnt++;
        }
    }

    int sum_cnt = (row_end - row_start + 1) * (row_end - row_start + 1);
    int row_mid = (row_start + row_end) / 2;
    int col_mid = (col_start + col_end) / 2;

    // 전부 흰색일 때
    if(w_cnt == sum_cnt) white++;
    // 전부 파란색일 때
    else if(b_cnt == sum_cnt) blue++;
    // 나눠야 할 때
    else {
        divide(row_start, row_mid, col_start, col_mid);
        divide(row_start, row_mid, col_mid + 1, col_end);
        divide(row_mid + 1, row_end, col_start, col_mid);
        divide(row_mid + 1, row_end, col_mid + 1, col_end);
    }
}


int main() {
    cin >> N;
    for(int i =0; i < N; i++) {
        for(int j = 0; j < N; j++) {
            cin >> arr[i][j];
        }
    }

    divide(0, N - 1, 0, N - 1);

    cout << white << endl << blue;
}

divide함수를 이용하여 분할정복을 구현하였다. for문을 사용하여 주어진 범위의 하얀색, 파란색 색종이의 개수를 구하였다. 전부 흰색이면 흰색 색종이 개수를 1 증가시키고 전부 파란색이면 파란색 색종이 개수를 1 증가시킨다. 흰색과 파란색이 공존하게 되면 이를 동일하지만 작은 문제로 나누는 방식을 재귀함수를 통해 구현하였다. (row_start ~ row_end) (col_start ~ col_end)를 가진 범위를 동일하게 4사분면으로 나누었다.

(row_start ~ row_mid) (col_start ~ col_mid)
(row_start ~ row_mid) (col_mid + 1, col_end)
(row_mid + 1 ~ row_end) (col_start ~ col_mid)
(row_mid + 1 ~ row_end) (col_mid + 1, col_end)

다음과 같이 조건을 나누게 되면 분할정복 구현이 완료된다.

---

느낀점

처음 분할정복을 구현하려고 했을 때는 재귀함수가 받는 파라미터를 나누는 것이 헷갈렸다. start, end를 잡고 무엇을 기준으로 작은 문제로 나누어야 하는지 고민하는 시간을 많이 가졌다. 이처럼 고민했던 시간이 조금 더 문제를 쉽게 풀 수 있도록 하지 않았나 싶다.