[Java] 알고리즘_Stack, DFS, BFS

✅ Stack

: 상자에 물건을 쌓아 올리듯이 데이터를 쌓는 자료 구조

🌐 특징

• 먼저 들어간 자료가 나중에 나옴 → 후입선출(LIFO, Last In First Out) 구조
• 인터럽트처리, 수식의 계산, 서브루틴의 복귀 번지 저장 등에 쓰임
• 그래프의 깊이 우선 탐색(DFS)에서 사용
• 재귀적(Recursion) 함수를 호출할 때 사용

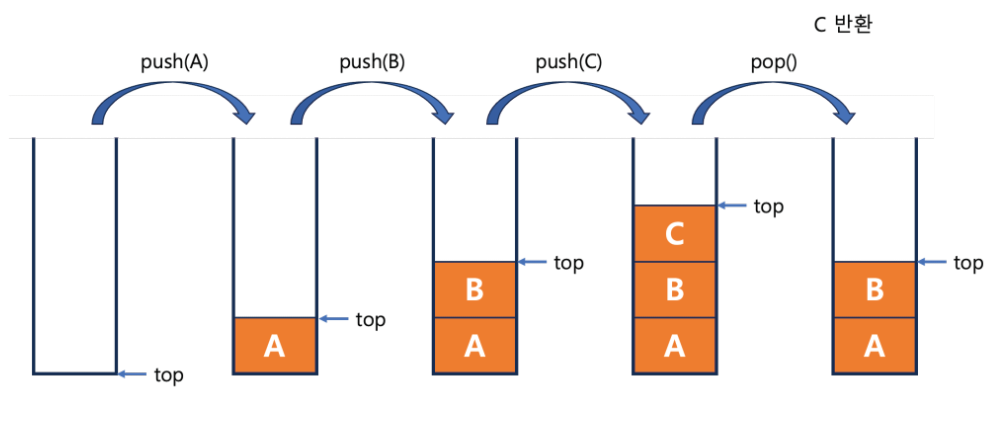
🌐 기능

• push() : 스택에 데이터를 추가
• pop() : 스택에서 데이터를 회수
• isEmpty() : 스택이 비어있는지 확인
• peek() : 스택의 제일 위에 무슨 자료가 있는지 확인
• isFull() : 스택이 가득 차 있는지 확인

🚧 예제 코드

public class StackEx {
	// 스택이 실제로 저장되는 곳
	private final int[] arr = new int[10];
    // 현재 스택의 최고점을 파악하기 위한 top
    priavte int top = -1;
    
    public StackEx() {}
    
    // push(): 데이터를 스택 제일 위에 넣는 메소드
    public void push(int data) {
    	// 1. arr[]가 가득 찼는지 판단
        if (arr.length - 1 == top) {
        	throw new RuntimeException("Stack is full");
        }
        // 2. 아니면 top을 하나 증가시킴
        top++;
        // 3. arr[top]에 data를 할당함
        arr[top] = data;
  	}
    
    // pop(): 데이터를 스택의 제일 위에서 회수하는 메소드
    public int pop() { // 언제나 제일 위에 있는걸 반환하니까 매개변수 필요 X
    	// 1. top을 기준으로 arr[]가 비어있는지 판단
        if (top == -1) {
        	throw new RuntimeException("Stack is empty");
       	}
        // 2. arr[top]의 값을 임시저장
        int temp = arr[top];
        // 3. top의 값을 하나 감소시킴
        top--;
        return temp;
        // 위 과정 정리한 것
        // return arr[top--];
     	
   	// peek(): 스택의 제일 위에 있는 데이터를 확인만하는 메소드
    public int peek() {
    	// 1. top을 기준으로 arr[]가 비어있는지 판단
        if (top == -1) {
        	throw new RuntimeException("Stack is empty");
       	}
        // 2. arr[top] 값 확인
        return arr[top];
   	}
    
    // isEmpty(): 스택이 비어있는지 확인하는 메소드
    public boolean isEmpty() {
    	// top이 -1일 때 비어있음
        return top == -1;
    }
    
    public static void main(String[] args) {
    	StackEx stack = new StackEx();
        // 스택에 3개의 데이터를 넣기
        stack.push(3);
        stack.push(5);
        stack.push(7);
        // 스택 맨 위에 데이터 확인하고 출력
        System.out.println(stack.peek());
        // 3개의 데이터 빼고 출력
        System.out.println(stack.pop());
        System.out.println(stack.pop());
        System.out.println(stack.pop());
        // 스택이 비어있는지 출력
        System.out.println(stack.isEmpty());
   	}
}

---

✅ Stack_DFS

: 깊이 우선 탐색(Depth-First Search), 그래프에서 깊은 부분을 우선적으로 탐색함

🌐 장단점

🔸 장점

• 구현이 너비 우선 탐색(BFS)보다 간단함
• 현재 경로 상의 노드들만 기억하면 되므로, 저장 공간의 수요가 비교적 적음
• 목표 노드가 깊은 단계에 있는 경우 빨리 구할 수 있음

🔹 단점

• 단순 검색 속도는 너비 우선 탐색(BFS)보다 느림
• 답이 없는 경우에 빠질 가능성이 있음
• 구한 답이 최단 경로가 된다는 보장이 없음

💡 동작 방식

1. 탐색 시작 노드를 스택에 삽입하고, 방문 처리
   
   
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리하고, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냄
   
   
3. 위의 1번과 2번 과정을 더 이상 수행할 수 없을 때까지 반복

🚧 예제 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class DepthFirstSearch {
    public void solution() throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        // 첫 입력은 정점의 갯수
        int maxNodes = Integer.parseInt(reader.readLine());
        // 정점간 연결 정보
        int[][] edgeMap = new int[maxNodes + 1][maxNodes + 1];

        // 1 2 1 3 2 4 2 5 4 6 5 6 6 7 3 7
        String[] edges = reader.readLine().split(" ");
        // 두개씩 순회
        for (int i = 0; i < edges.length / 2; i++) {
            int leftNode = Integer.parseInt(edges[i * 2]);  // 0, 2, 4, ...
            int rightNode = Integer.parseInt(edges[i * 2 + 1]);  // 1, 3, 5, ...
            edgeMap[leftNode][rightNode] = 1;
            edgeMap[rightNode][leftNode] = 1;
        }

        // 다음에 방문할 점들을 담아두는 스택
        Stack<Integer> toVisit = new Stack<>();
        // 방문을 기록하는 용도의 배열
        boolean[] visited = new boolean[maxNodes + 1];
        // 여기부터 DFS

        // TODO 방문 순서를 출력하는 문제라 가정
        // TODO 방문 순서를 담기위한 List
        List<Integer> visitedOrder = new ArrayList<>();

        // 첫 방문 대상 선정 (1)
        int next = 1;
        // 대상을 스택에 push
        toVisit.push(next);
        // 스택이 빌때까지 반복하는 while
        while (!toVisit.empty()) {
            // TODO 다음 방문할 곳을 가져온다. (pop)
            next = toVisit.pop();

            // TODO 이미 방문했다면 다음곳으로 간다. (pop)
            if (visited[next]) continue;

            // TODO 방문했다 표시한다.
            visited[next] = true;

            // TODO 요부분은 문제에 따라 다르다.
            visitedOrder.add(next);

            // TODO 다음 방문 대상을 검색해서, 스택에 푸시 한다.
            // 더 작은 숫자부터 방문하려면 스택에 역순으로 넣는다.
            for (int i = maxNodes; i > 0; i--) { // TODO 그래프에 존재하는 정점들을 순회
                // TODO 해당 정점에 도달할 수 있고, 아직 방문하지 않았다면
                if (edgeMap[next][i] == 1 && !visited[i]) {
                    // TODO 다음에 방문할 곳으로 스택에 푸시
                    toVisit.push(i);
                }
            }
        }

        // TODO 답을 출력한다.
        System.out.println(visitedOrder);
    }

    public static void main(String[] args) throws IOException {
        new DepthFirstSearch().solution();
    }
}

---

✅ Queue_BFS

: 너비 우선 탐색(Breadth-First Search),기준노드에서 인접한 노드를 먼저 탐색

👉 주로 두 지점의 최단경로 및 임의의 경로를 찾고싶을 때 사용

🌐 특징

• 직관적이지 않음
• 어떤 노드를 방문했는지 반드시 확인해야함 → 무한 루프 방지
• 방문한 노드를 차례로 저장한 후 꺼내는 Queue 자료구조 사용
  

💡 동작 방식

1. 방문한 점에서 도달할 수 있는 점들을 살펴보고, 아직 방문하지 않은 점들을 큐에 enQueue함
2. 큐에서 점의 정보를 deQueue하고 방문하고, 이후 다시 1번으로 돌아감
3. 큐가 빌때까지 반복

🚧 예제 코드

public BFS {
	public void solution() throws IOException {
    	BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        int maxNodes = Integer.parseInt(reader.readLine());
        // 인접 정보 저장용
        int[][] adjMap = new int[maxNodes + 1][maxNodes + 1];
        
        String[] edges = reader.readLine().split(" ");
        for(int i = 0; i < edges.length / 2; i++) {
        	int leftNode = Integer.parseInt(edge[i * 2]); // 0, 2, 4 ...
            int rightNode = Integer.parseInt(edge[i * 2 + 1]); // 1, 3, 5 ...
            adjMap[leftNode][rightNode] = 1;
            adjMap[rightNode][leftNode] = 1;
       	}
        
        // 다음 방문 대상 기록용 Queue
        Queue<Integer> toVisit = new LinkedList<>();
        // 방문 순서 기록용 List
        List<Integer> visitedOrder = new ArrayList<>();
        // 방문 기록용 boolean[]
        boolean[] visited = new boolean[maxNodes + 1];
        
        int next = 1;
        toVisit.offer(next);
        while(!toVisit.isEmpty()) {
        	// 다음 방문 정점 회수
            next = toVisit.poll();
            // 이미 방문 했다면 다음 반복으로
            if (visited[next]) continue;
            // 방문했다 표시
            visited[next] = true;
          	// 방문한 순서 기록
            visitOrder.add(next);
            
            // 다음 방문 대상을 검색
            for (int i = 0; i < maxNodes + 1; i++) {
            	// adjMap[next]가 담고 있는 배열은
                // idx번째가 1인 경우 idx에 연결되어있다는 뜻
                if (adjMap[next][i] == 1 && !visited[i])
                	toVisit.offer(i);
           	}
       	}
        // 출력
        System.out.println(visitedOrder);
   	}
    
    public static void main(String[] args) throws IOException {
    	new BFS().solution();
	}
}

👉 결과