[Java] 알고리즘_Tree

✅ Tree

👉 한개 이상의 노드로 이루어진 유한 집합

• 노드 중 최상위 노드를 루트 노드(root)라고 함
• 각각 데이터를 담고 있는 원소를 노드 또는 정점이라고 함
• 각 노드는 0개 이상의 자식노드를 가질 수 있음
• 자식 노드를 가지고 있지 않은 노드를 단말노드 또는 잎노드(leaf)라고 함
• 자식 원소는 둘 이상의 부모 원소를 가질 수 없음
• 노드 개수가 n개면, 간선의 개수는 n-1개가 됨

✅ Tree_이진 트리

👉 모든 부모 노드가 최대 2개의 자식 노드를 가진 트리

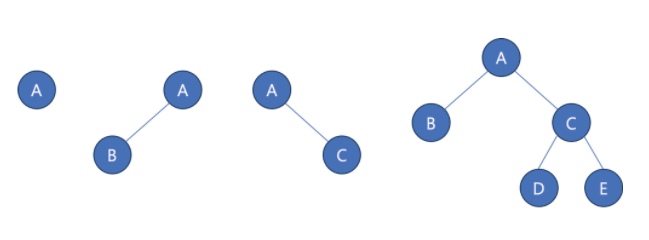
• 레벨*이 i인 노드의 개수는 최대 2^i 개임
  (레벨: 트리의 깊이. 노드의 높이 = 간선의 개수)
• 트리 전체 노드의 최소 개수는 h+1 개이고, 최대 개수는 2^(h+1)-1 개임

🔹 포화 이진 트리 (Perfect Binary Tree)

👉 모든 레벨에 노드가 최대로 차있는 이진 트리
→ 높이가 h일때, 최대 노드 개수: 2^(h+1)-1

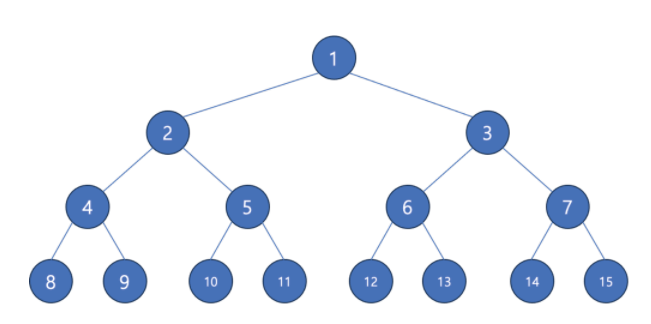
🔹 완전 이진 트리 (Complete Binary Tree)

👉 마지막 레벨을 제외한 노드가 최대 개수이며, 마지막 레벨의 노드는 왼쪽부터 채워진 이진트리

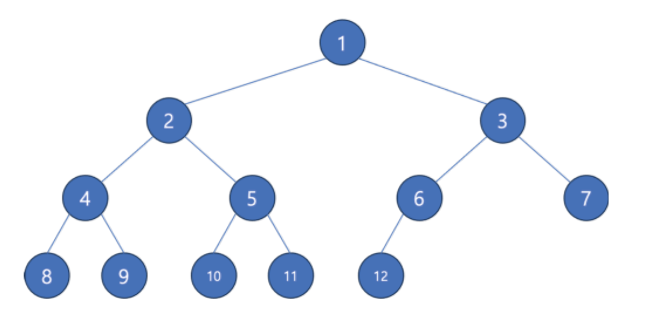
🔹 편향 이진 트리 (Skewed Binary Tree)

👉 이진 트리 조건을 유지하면서, 최소 노드의 개수로 한쪽 방향의 자식 노드만 가지는 이진 트리

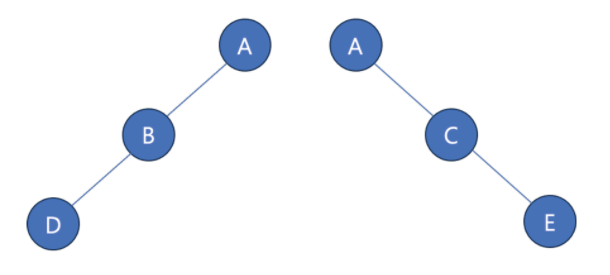
🌐 이진 탐색 트리 (Binary Search Tree)

• 모든 노드의 데이터가 서로 다른 이진 트리
• 어느 노드의 자식이 있을 경우
  • 왼쪽 자식 데이터는 부모 노드 데이터보다 항상 작음
  • 오른쪽 자식 데이터는 부모 노드 데이터보다 항상 큼
• 위 규칙이 재귀적으로 적용되기 때문에,
  • 왼쪽 서브 트리 모든 데이터 < 루트 노드
  • 오른쪽 서브 트리 모든 데이터 > 루트 노드
• 중위 순회하면 데이터가 오름차순으로 정렬됨

🚧 예제 코드

• insert() : 데이터를 BST에 추가
• search() : 어떤 데이터가 BST에 존재하는지 판단
• delete() : 데이터를 BST에서 제거

public class BST {
	private static class Node {
    	private int key;
        pirvate Node left;
        private Node right;
        
        public Node(int key) {
        	this.key = key;
            left = null;
            right = null;
      	}
   	}
    
    pirvate Node root;
    
    public BST() {
    	this.root = null;
    }
    
    // 삽입 메소드
    public void insert(int key) {}
    
    // 삽입 메소드에서 재귀호출할 메소드
    public Node insertNode(Node node, int key) {
    	// node가 null이면 -> 부모 노드의 자식 노드가 null -> 삽입
        if (node == null) {
        	node = new Node(key);
            return node;
       	}
        
        if (node.key == key) {
        	// 탐색에 성공한 경우 더이상 확인 X
            return node;
        }
        
        // 재귀호출
        // 현재 노드보다 데이터가 작을 경우 왼쪽 트리로 이동
    	if (key < node.key) {
        	node.left = insertNode(node.left, key);
       	}
        
        // 재귀호출
        // 현재 노드보다 데이터가 클 경우 오른쪽 트리로 이동
        if (key > node.key) {
        	node.right = inserNode(node.right, key);
       	}
        
        // 삽입 X => 본래 자식 그대로 반환
        return node;
	}
    
    // 탐색 메소드
    public boolean search(int key) {
    	return searchNode(root, key);
   	}
    
    // 탐색 재귀함수
    private boolean searchNode(Node node, int key) {
    	// 현재 노드가 null인 경우
        if (node == null) {
        	return false;
       	}
        
        // 탐색 성공
        if (key == node.key) {
        	return true;
       	}
        
        // 재귀호출
        // 현재 노드보다 데이터가 작을 경우
        if (key < node.key) {
        	// 왼쪽 서브 트리 탐색 결과 반환
            return searchNode(node.left, key);
       	}
        
        // 현재 노드보다 데이터가 클 경우
        else (key > node.key) {
        	// 오른쪽 서브 트리 탐색 결과 반환
            return searchNode(node.right, key);
       	}
  	}
    
    // 삭제 메소드
    public void delete(int key) {
    	root = deleteNode(root, key);
   	}
    
    // 삭제 재귀함수
    private Node deleteNode(Node node, int key) {
    	// 없는 노드는 돌아감
        if (node == null) {
        	return null;
       	}
        
        // 노드의 값이 삭제 대상보다 작을 경우
        if (key < node.key) {
        	// 왼쪽 노드로 감
            // 삭제 결과에 따라 자식이 갱신될 수 있음
            node.left = deleteNode(node.left, key);
       	}
        
        // 노드의 값이 삭제 대상보다 클 경우
        else if (key > node.key) {
        	// 오른쪽 노드로 감
            // 삭제 결과에 따라 자식이 갱신될 수 있음
            node.right = deleteNode(node.right, key);
       	}
        
        // 현재 노드가 삭제 대상일 경우
        else {
        	if (node.left == null) return node.right;
            else if (node.right == null) return node.left;
            
            두 자식이 다 있다면
            // 오른쪽 서브트리 가장 작은 값을 찾아 현재 노드에 할당
            node.key = minValue(node.right);
            // 그 값을 가지는 노드를 제거
            node.right = deleteNode(node.right, node.key);
      	}
        
        // 현재 노드를 다시 반환
        return node;
   	}
            	
           
    
    // 중위 순회
    public void inorderTraversal() {
    	indorder(root);
   	}
    
    private void inorder(Node node) {
    	if (node != null) {
        	inorder(node.left);
            System.out.println(node.key + " ");
            inorder(node.right);
       	}
   	}