백준 16724 - 피리 부는 사나이

문제

피리 부는 사나이 성우는 오늘도 피리를 분다.

성우가 피리를 불 때면 영과일 회원들은 자기도 모르게 성우가 정해놓은 방향대로 움직이기 시작한다. 성우가 정해놓은 방향은 총 4가지로 U, D, L, R이고 각각 위, 아래, 왼쪽, 오른쪽으로 이동하게 한다.

이를 지켜보던 재훈이는 더 이상 움직이기 힘들어하는 영과일 회원들을 지키기 위해 특정 지점에 ‘SAFE ZONE’ 이라는 최첨단 방음 시설을 만들어 회원들이 성우의 피리 소리를 듣지 못하게 하려고 한다. 하지만 예산이 넉넉하지 않은 재훈이는 성우가 설정해 놓은 방향을 분석해서 최소 개수의 ‘SAFE ZONE’을 만들려 한다.

성우가 설정한 방향 지도가 주어졌을 때 재훈이를 도와서 영과일 회원들이 지도 어느 구역에 있더라도 성우가 피리를 불 때 ‘SAFE ZONE’에 들어갈 수 있게 하는 ‘SAFE ZONE’의 최소 개수를 출력하는 프로그램을 작성하시오.

입력

첫 번째 줄에 지도의 행의 수를 나타내는 N(1 ≤ N ≤ 1,000)과 지도의 열의 수를 나타내는 M(1 ≤ M ≤ 1,000)이 주어진다.

두 번째 줄부터 N개의 줄에 지도의 정보를 나타내는 길이가 M인 문자열이 주어진다.

지도 밖으로 나가는 방향의 입력은 주어지지 않는다.

출력

첫 번째 줄에 ‘SAFE ZONE’의 최소 개수를 출력한다.

예제 입력

3 4
DLLL
DRLU
RRRU

예제 출력

2

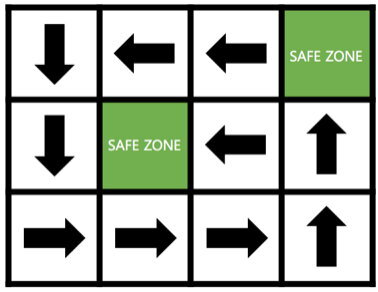
다음과 같이 'SAFE ZONE'을 만들면 영과일 회원들이 지도 어느 구역에 있더라도 'SAFE ZONE'에 들어갈 수 있다.

---

발판이 복잡해보여 처음 봤을 땐 이해하기 어려웠지만,
조건 중 '지도 밖으로 나가는 방향의 입력은 주어지지 않는다.' 가 큰 힌트였다.

결국 나올 수 있는 발판은
1. 계속 돌거나
2. 도는 곳에 끼어서 돌게 되거나
둘 중 한가지이다.

두 가지 경우 모두 하나의 SAFE ZONE으로 동시에 해결할 수 있기 때문에 (돌던 곳 중 하나만 두면 OK),
결국 생기는 사이클의 개수를 구하는 문제였다.

기본적으로 부분집합 알고리즘인 부모를 찾아가는 과정을 사용했고,
각 발판에 번호를 주고, 발판에 맞는 부모 발판의 번호 또한 저장하도록 만들었다.

어느 지점이던, 사이클이 생긴다면(visited[x]의 값이 true로 바뀐 지역에 다시 도착할 경우), 모든 부모를 x로 맞춘다.
이미 사이클이 생긴 발판인지, 아닌지를 구분하기 위해

부모 발판과, 부모의 부모 발판을 비교했다.그 둘이 같다면, 사이클은 모두 같은 부모를 갖고있기 때문에 이미 만들어진 사이클이므로 부모값만 같게 맞추고,다르다면, 새로운 사이클이므로 SAFE ZONE의 수를 늘리고 새로운 사이클에 해당하는 모든 발판의 부모를 그 위치로 맞춘다.

// visited는 초기화하지 않는다.
int findParents(int x){
  if(visited[x]){
    if(parents[x] == parents[parents[x]]){
      return parents[x];
    }

    else {
      SAFE_ZONE++;
      return x;
    }
  }
  visited[x] = true;
  return parents[x] = findParents(parents[x]);
}

마지막 메모이제이션 과정이 사이클의 부모를 맞추는 과정과 속도를 동시에 해결했다.

모든 코드:

#include <iostream>

using namespace std;

int parents[1000000];
bool visited[1000000];
int SAFE_ZONE = 0;

/* 
visited를 채워가며 parents를 찾는 중,
(visited[x]) 인 x에 대해 그 점을 parents로 하며
(!visited[y]) 를 만족하는 y를 찾아 다시 parents를 구한다.
parents[x] 가 비었다면 SAFE ZONE의 수를 1 늘리고
parents[x] 가 이미 존재한다면 SAFE ZONE의 수를 유지한다.
*/

int findParents(int x){
  if(visited[x]){
    if(parents[x] == parents[parents[x]]){
      return parents[x];
    }

    else {
      SAFE_ZONE++;
      return x;
    }
  }
  visited[x] = true;
  return parents[x] = findParents(parents[x]);
}

int main() {
  cin.tie(NULL);
  ios_base::sync_with_stdio(false);
  int N, M;
  cin >> N >> M;
  char board[N][M];
  int idx[N][M];
  fill(visited, visited + N * M, false);

  int stack = 0;
  for(int i = 0; i < N; i++){
    for(int j = 0; j < M; j++){
      cin >> board[i][j];
      idx[i][j] = stack;
      switch(board[i][j]){
        case 'L':
        parents[idx[i][j]] = stack - 1;
        break;
        case 'R':
        parents[idx[i][j]] = stack + 1;
        break;
        case 'U':
        parents[idx[i][j]] = stack - M;
        break;
        case 'D':
        parents[idx[i][j]] = stack + M;
        break;
        default: break;
      }
      stack++;
    }
  }
  
  for(int i = 0; i < N * M; i++){
    if(!visited[i]) findParents(i);
  }

  cout << SAFE_ZONE <<"\n";
}