동적 계획법

피보나치 수열

피보나치 수열의 i번째 값을 계산하는 F를 정의하면

F(0) = 0, F(1) = 1
F(i) = F(i-1) + F(i-2) for i >= 2 라고 할 수 있다.

이는 재귀 함수로 구현할 수 있다.

f(n+2) = f(n) + f(n+1)
→ f의 0 번째와, 1번째는 알고 있어야 문제를 풀어갈 수 있다.

public class 피보나치 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		
		int N = sc.nextInt();
		
		
		System.out.println(fibo(N));
	}
	
	public static int fibo(int n) {
		if(n < 2 ) return n;
		return fibo(n-1) + fibo(n-2);

	}
}

Memoization

• 컴퓨터 프로그램을 실행할 때, 이전에 계산한 값을 메모리에 저장하여 매번 다시 계산하지 않다록 하여 실행 속도를 빠르게 하는 기술

• 값을 구하지 않았다면, 재귀로 호출하고, 이미 계산을 했다면 리턴한다.
• 내려가면서 접근하므로, 하향식 접근 방법이다.

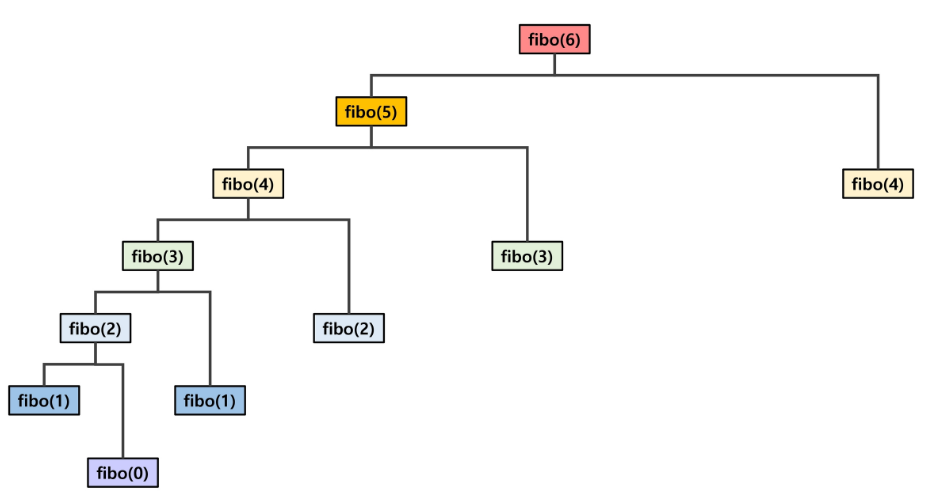
동적 계획 알고리즘

• 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘
• 작은 부분 문제들을 해결하여, 최종적으로 큰 크기의 문제들을 해결하여 원래 주어진 문제를 해결하는 방법

필요 조건

• 중복 부분문제 구조
  • 큰 문제를 해결하기 위해서, 작은 문제를 최적해를 이용해 순환적으로 해결
  • 이러한 순환적 성질 때문에, 이전에 계산이 되었던 작은 문제의 해를 어딘가에 저장하게 된다.
  • 이렇게 저장된 해들이 다시 필요할 때마다, 매번 계산이 아닌 저장 공간의 참조를 통해 중복 계산을 피한다.

• 최적 부분문제 구조
  • 주어진 문제가 최적화의 원칙을 만족해야, 동적 계획법을 효율 적으로 적용할 수 있다는 의미
  • 어떤 문제에 대한 해가 최적일 때, 그 해를 구성하는 작은 문제들의 해 역시 최적이어야 한다는 뜻
  • 원칙이 적용되지 않는 예 : 최장 경로의 문제

분할 정복과 동적 계획법의 비교

구분	분할 정보	DP
문제 해결 방식	- 연관 없는 부분 문제로 분할한다.	- 부분 문제들이 연관이 없으면 적용할 수 없다.
	- 부분문제를 재귀적으로 해결한다.	- 모든 부분 문제를 한번만 계산하고, 결과를 저장하고 재사용한다.
	- 부분문제의 해를 결합(Combine)한다.	- (분할 정보와 같은 부분 문제가 나타날 경우 다시 계산한다.)
예시	- 병합정렬 / 퀵정렬	- 피보나치 수열, 최장 공통 부분 수열 등
접근방법	- 하향식 방법	- 상향식 방법

DP 접근 방법

1. 최적해 구조의 특성을 파악해라 : 문제를 부분 문제로 나눈다..
2. 최적해의 값을 재귀적으로 정의해라 : 부분 문제의 최적해 값에 기반하여 문제의 최적해 값을 정의
3. 상향식 방법으로 최적해 값 계산
   • 가장 작은 부분 문제부터 해를 구한 후 테이블에 저장
   • 테이블에 저장되어 있는 부분 문제의 해를 이용하여 점차적으로 상의 부분 문제의 최적해 구하기

자바 구현

public static int fibo3(int n) { // 피보나치
	int[] dp = new int[n+1];
	dp[0] = 0;
	dp[1] = 1;
	for(int i = 2; i <= n; i++) {
		dp[i] = dp[i-1] + dp[i-2];
	}
	return dp[n];
}

실행 속도가 빠르다

• 재귀 알고리즘과 달리 중복 계산이 없다.
• 반복문을 사용하기 때문에 함수 호출이 발생하지 않기 때문

예시1 > 동전 거스름돈

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
		
	int money = sc.nextInt();
	int[] dp = new int[money+1];
		
	// 동전의 종류가 1, 4, 6일 때, 최소 개수로 거스름돈을 줄 수 있는 방법 
		
	for(int i = 1; i <= money; i++) {
		int min = Integer.MAX_VALUE;
		min = Math.min(min, dp[i-1]+1); // 거스름돈이 1원인 경우
			
		if(i >= 4) min = Math.min(min, dp[i-4]+1); // 거스름돈이 4원인 경우
		if(i >= 6) min = Math.min(min, dp[i-6]+1); // 거스름돈이 6원인 경우
		dp[i] = min;
	}
		
	System.out.println(dp[money]);
}

예시2 > 가방 챙기기

• 먼저 배낭 문제의 부분 문제를 찾아내기 위해 문제의 주어진 조건 살펴보기
• 물건, 물건의 무게, 물건의 가치, 배낭의 용량, 모두 4가지의 요소가 있다.
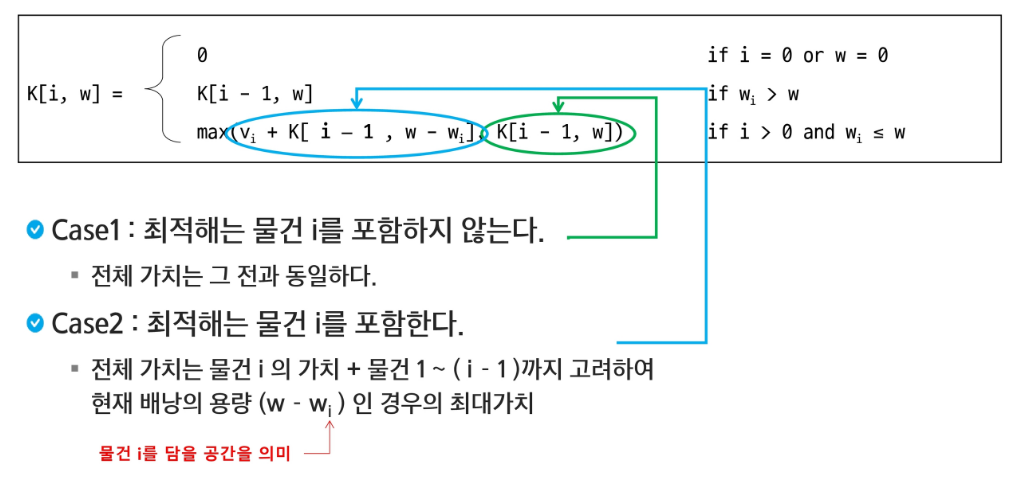
  이 중에서 물건과 물건의 무게는 부분 문제를 정의하는 반드시 필요하다.
• 배낭이 비어 있는 상태에서 시작하여 물건을 하나씩 배낭에 담는 것과 안 담는 것을 현재 배낭에 들어 있는 물건의 가치의 합에 근거하여 결정해야 하기 때문이다.
• 또한 물건을 배낭에 담으려고 할 경우에 배낭 용량의 초과 여부를 검사해야 한다.

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
		
	int N = sc.nextInt(); // 물건의 개수 
	int W = sc.nextInt(); // 배낭의 무게 
		
	int[] weight = new int[N+1];
	int[] cost = new int[N+1];
		
	for(int i = 1; i <= N; i++) {
		weight[i] = sc.nextInt();
		cost[i] = sc.nextInt();
	}
		
	int[][] dp = new int[N+1][W+1];
		
	for(int i = 1; i <= N; i++) {
		// 각 종류의 물건은 하나씩만 담을 수 있다는 조건 
		for(int w = 0; w <= w; w++) {
			// w는 임시 무게가 된다. 
			// 고려할 물건의 무게가 임시 무게보다 작다면 
			if(weight[i] <= w) {
				dp[i][w] = Math.max(dp[i-1][w], dp[i-1][w-weight[i]+cost[i]]);
			} else {
				dp[i][w] = dp[i-1][w];
			}
		}
	}
	
	System.out.println(dp[N][W]);
}