APS

APS - Algorithm Problem Solving 문제를 해결하기 위해 수행해야 하는 절차나 방법 목표 : 다양한 알고리즘을 이해하고 문제의 조건에 맞는 좋은 알고리즘을 선택할 수 있게 되는 것 순서를 정확하게 이해하고 그에 맞춰 진행하는 것이 필요하다. 알고

저장되어 있는 자료 중 원하는 항목을 찾는 작업 종류순차 검색이진 검색인덱싱 (데이터 베이스에서 검색하는 방법) 일렬로 되어있는 자료를 순서대로 검색하는 방법 배열이나 연결 리스트 등 순차구조로 구현된 자료구조에서 원하는 항목을 찾을 때 유용단순하여 구현이 쉽지만, 검

배열 : 동일한 자료형의 data를 여러 개 담을 수 있는 자료 구조 2차원 배열은 1차원 배열 들을 담을 수 있는 배열이다. 배열은 JVM의 heap 영역에 들어간다. 2차원 배열의 경우, 1차원 배열이, 행의 갯수만큼 생성이 된 후 그것들을 호출하는 방식이 된다.

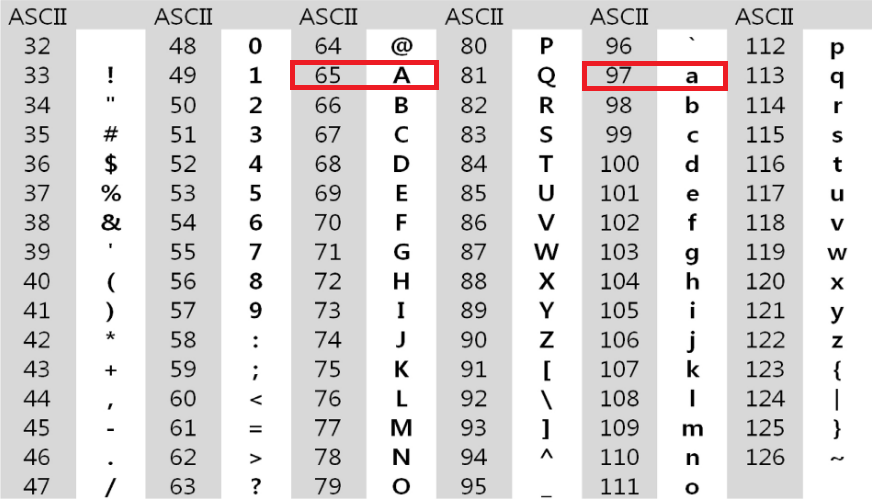
참조 자료형으로 문자를 여러 개 담을 수 있는 구조비트 단위로 저장하므로 문자를 직접 저장할 수 없다, 따라서 정수의 형태로 문자와 짝지어진 수를 저장000000 → 'A' 000001 → 'B'코드 체계가 달라 발생하는 혼동을 막기 위해 생긴 것이 ASCII 코드 A

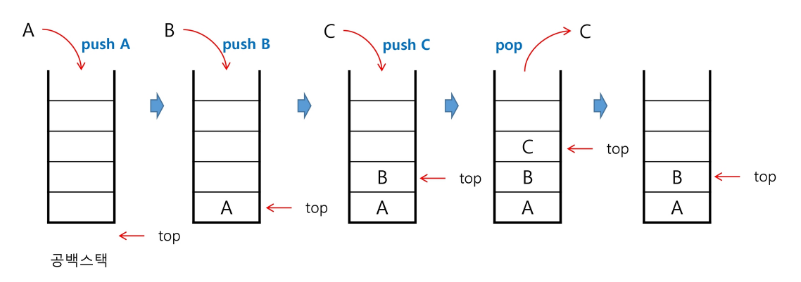
물건을 쌓아 올리듯, 자료를 쌓아 올리는 형태의 자료구조이다. 스택에 저장된 자료는 선형 구조를 갖는다. 선형 구조 : 자료 간의 관계가 1대 1의 관계를 갖는다. 비선형 구조 : 자료 간의 관계가 1대 N의 관계를 갖는다. (예: 트리) 자료를 삽입하거나 꺼내는 용도

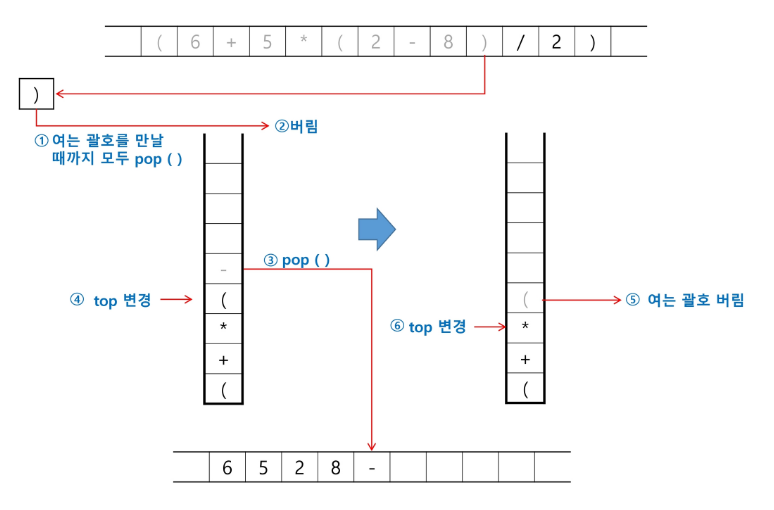
중위 표기식을 후위 표기식으로 변환 (스택 활용) 후위 표기식을 계산 (스택 활용) 문자열로 된 계산식이 주어질 때, 스택을 이용하여 이 계산식의 값을 계산할 수 있다. 중위 표기법 : 연산자를 피연산자의 가운데에 표기 (A+B) 후위 표기법 : 연산자를 피연산자 뒤에

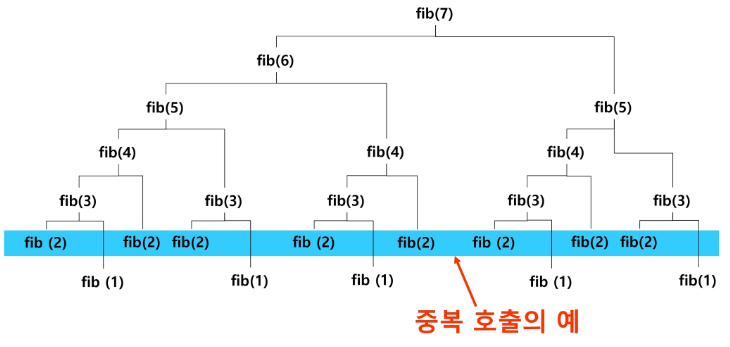
자기 자신을 호출하여 순환 수행되는 것 함수 호출은 메모리 구조에서 스택을 사용한다. (이름만 같은 메서드)기본 부분 : 재귀 호출에서 빠져 나가기 위한 조건 재귀 부분 : 자신을 호출하는 부분 (기본 부분으로 유도한다.) 재귀적 프로그램을 작성하는 것은, 반복 구조에

스택과 마찬가지로 삽입과 삭제의 위치가 제한적인 자료 구조 선형큐와 원형큐(환원큐) 의 종류로 나뉜다.FIFO 구조 enQueue(item) : 큐의 가장 꼬리에 원소를 삽입하는 연산 deQueue() : 큐의 앞쪽에서 원소를 삭제하고 반환하는 연산createQueu

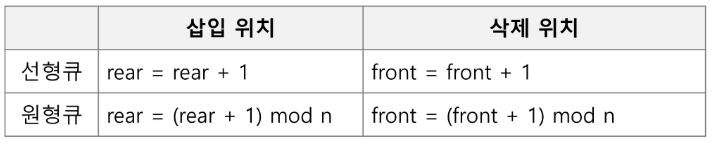
잘못된 포화상태 인식을 해결하기 위해서 등장 front와 rear의 위치가 배열의 마지막 인덱 n-1을 가리킨 후, 그 다음 논리적 순환을 이루어 배열의 처음인 0으로 이동 → 이를 위해 나머지 연산자 %를 사용 선형 큐를 구하던 때와 동일한 방식을 사용하게 되면, 공

연결리스트 자료의 논리적인 순서와 메모리 상의 물리적인 순서가 일치하지 않고, 개별적으로 위치하고 있는 원소의 주소를 연결하여 하나의 전체적인 자료구조를 이룬다. 논리적 구조 : 사람이 이해하는 구조 물리적 구조 : 실제 메모리 상에 저장되는 구조 링크를 통해

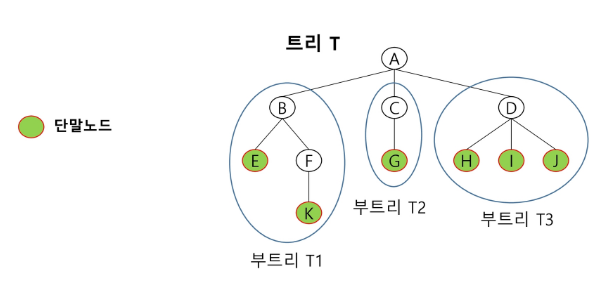
비선형 구조 원소들 간에 1:N 관계를 갖는 자료구조 원소들 간에 계층 관계를 갖는 계층형 자료구조 상위 원소에서 하위 원소로 내려가면서 확장되는 트리 모양의 구조 한 개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다. 노드 중 최상위 노드를 root라고

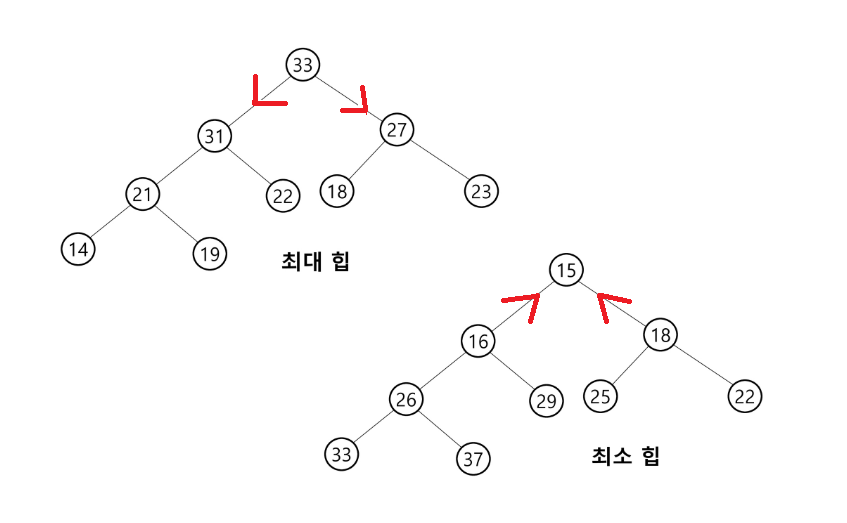
완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 구조 최대 힙키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리 부모 노드의 키 값 >= 자식 노드의 키 값 루트 노드 : 키 값이 가장 큰 노드 최소 힙 키 값이

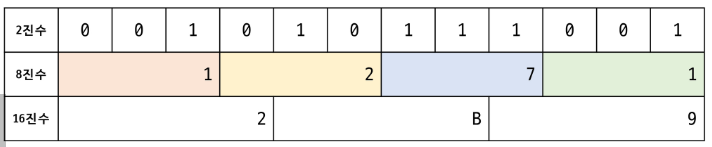
수를 표현하는 기수법의 하나 10진법진수가 10인 진법 0 - 9까지의 10개 숫자를 사용 2진법의 경우, 컴퓨터 내부에서 데이터를 처리하는 데 주로 사용한다. 8진법은 과거에 컴퓨터 시스템에서 메모리 주소를 간략하게 표현하기 위해 사용했지만, 이제는 16진법을 사용한

모든 경우에 대해서 검색하는 방법 부분집합주어진 집합의 원소 중 일부 또는 전체를 포함하는 집합공집합(아무것도 없는) 또한 부분집합의 일부가 된다.집합의 원소가 N개일 때, 부분 집합의 수는 2N 개가 된다. 부분 집합의 구현 비트로 보게 된다면 1<<N이

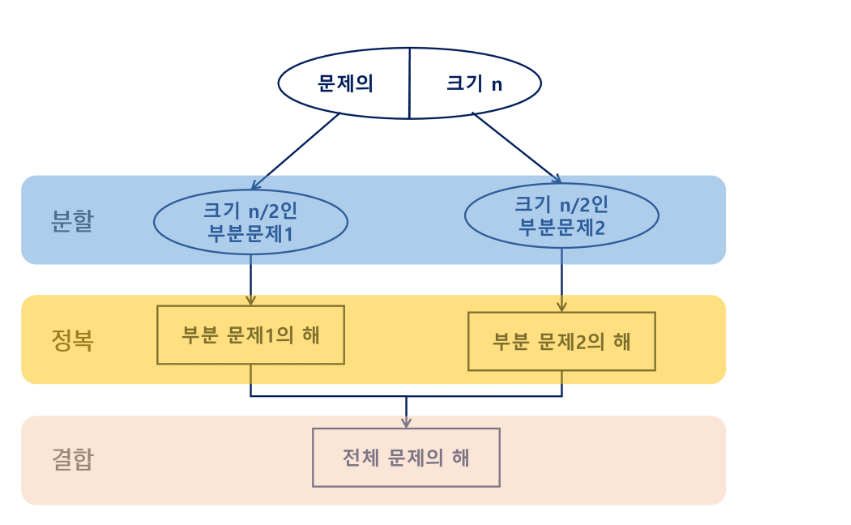
큰 문제를 작은 하위 문제로 나누어 해결하는 방식 설계 전략 분할 : 해결할 문제를 여러 개의 작은 부분으로 나눈다.정복 : 나눈 작은 문제를 각각 해결한다.결합 : 해결된 해답을 모은다. 자바 구현이미 정렬된 배열에서 특정한 값을 빠르게 찾기 위한 알고리즘 검색 범위

가능한 모든 경우를 탐색하는 중 해답으로 이어지지 않는 경우에 대해서 탐색하지 않고 되돌아가며 해결유망 : 현재 상태가 문제의 해답으로 발전한 가능성이 높은지를 판단하는 기준가지치기 : 탐색 중 불필요한 경로를 제거하여 탐색의 효율성을 높이는 방법 유망성이 없는 가정은

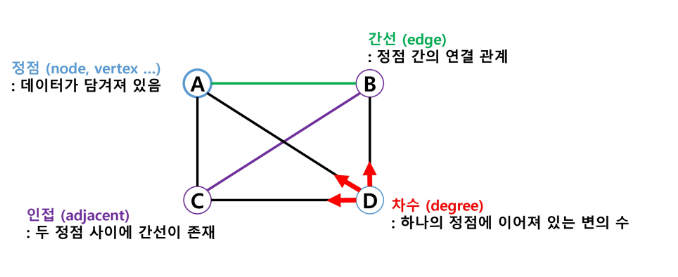
아이템(사물 또는 추상적 개념) 들과 이들 사이의 연결 관계 표현 정점들의 집합과 이를 연결하는 간선들의 집합 선형자료구조나 트리로 표현하기 어려운 M:N의 관계를 표현한 것이다. V개의 정점을 가지는 그래프는 최대 V\*(V-1)/2 간선이 가능

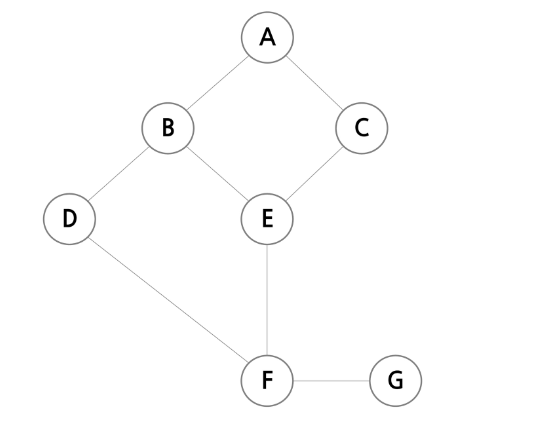
모든 노드를 빠짐 없이 탐색하는 방법은 두 가지가 있다. 깊이 우선 탐색(Depth First Search, DFS)너비 우선 탐색 (Breadth First Search, BFS) 시작 시점에서 출발하여 한 방향으로 탐색진행할 수 없는 상황이 온다면, 마지막 만난 지

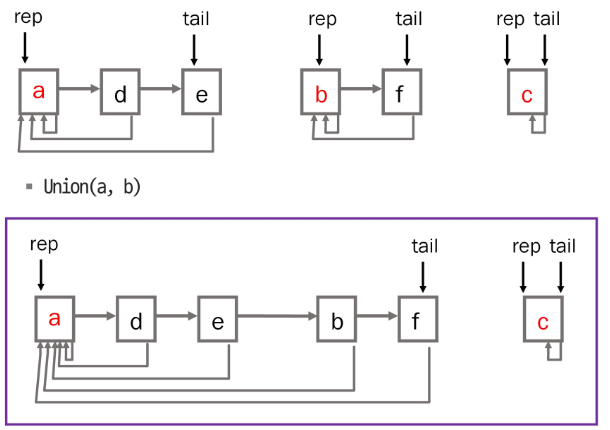
중복 포함된 원소가 없는 집합 → 교집합이 없다. 각 집합은 대표자를 통해 구분 표현 방법 연결 리스트트리상호 배타 집합 연산 Make-Set(X) : X라고 하는 원소를 대표자로 하는 집합 생성 Find-Set(x) : x가 속한 대표 집단 찾기 Union(x,y)

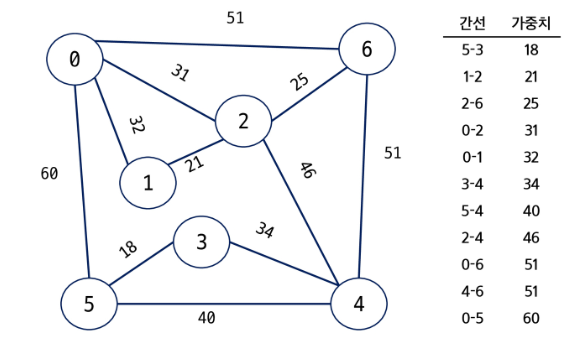
신장 트리 : 그래프의 모든 정점과 간선의 부분 집합으로 구성되는 트리 간선의 갯수는 노드 갯수 - 1 이 된다. 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 트리 무 방향 가중치 그래프 N개의 정점을 가지는 그래프에 대해서 반드시 (N - 1)개의 간선을 사

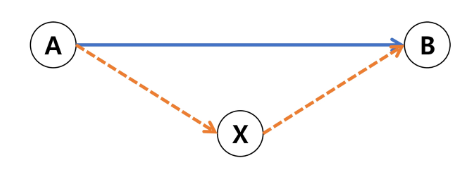
최소 신장 트리 : 모든 정점을 연결하며 사이클이 없는 트리 하나의 정점에서 연결된 간선 중에 하나씩 선택하면서 최소 신장 트리를 만들어 가는 방식 임의 정점을 선택해서 시작 (크루스칼은 간선을 선택하면서 진행한다.) ※ 모든 정점을 선택할 것이기 때문에, 정점의 선택

진입 차수 : 특정 노드로 들어오는 간선의 개수 진입 차수가 0인 경우, 선행 조건이 없는 노드라고 한다. 진출 차수 : 특정 노드에서 나가는 간선의 개수 위상 정렬 순서가 있는 작업을 차례로 진행해야 할 때 순서를 정해주기 위해 사용하는 알고리즘 사이클 없는 방향 그래프(DAG)의 모든 노드를 주어진 방향성에 어긋나지 않게 순서를 나열하는 것 ex...

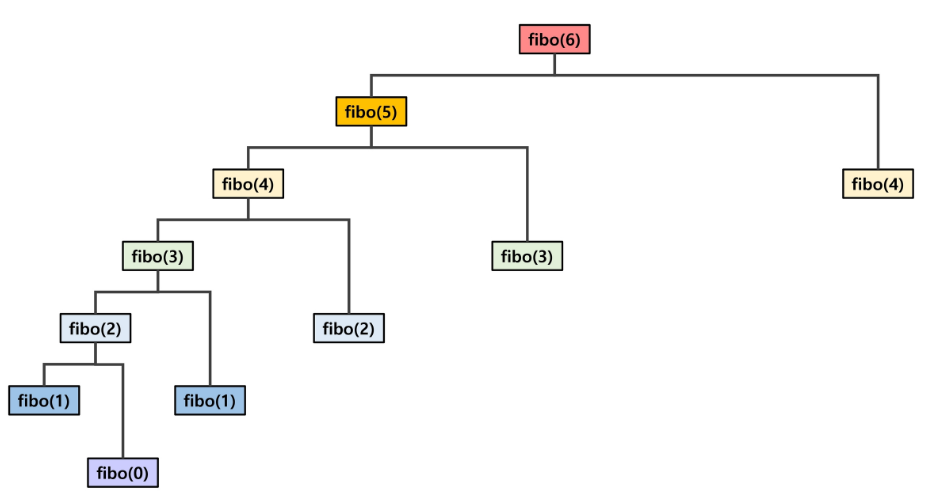
피보나치 수열의 i번째 값을 계산하는 F를 정의하면 F(0) = 0, F(1) = 1F(i) = F(i-1) + F(i-2) for i >= 2 라고 할 수 있다. 이는 재귀 함수로 구현할 수 있다. f(n+2) = f(n) + f(n+1) → f의 0 번째와, 1번째