Queue - 2

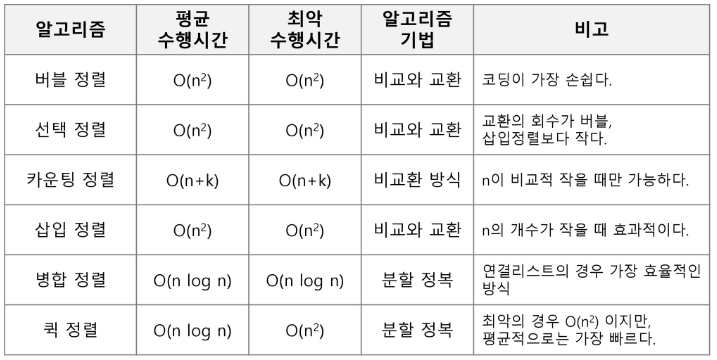
원형 큐

잘못된 포화상태 인식을 해결하기 위해서 등장

• front와 rear의 위치가 배열의 마지막 인덱 n-1을 가리킨 후, 그 다음 논리적 순환을 이루어 배열의 처음인 0으로 이동
  → 이를 위해 나머지 연산자 %를 사용
• 선형 큐를 구하던 때와 동일한 방식을 사용하게 되면, 공백 상태와 포화 상태 구분이 쉽지 않게 된다.
• 따라서, 원형 큐의 경우, front가 있을 한 자리를 영구적으로 비워두게 된다.
• 인덱스들이 순환하는 구조로 만들기 위한 것

• 포화 상태를 확인하는 조건 : front가 rear의 한 칸 앞인지. (N + front - rear) % 4 == 1
  (N : 배열 크기)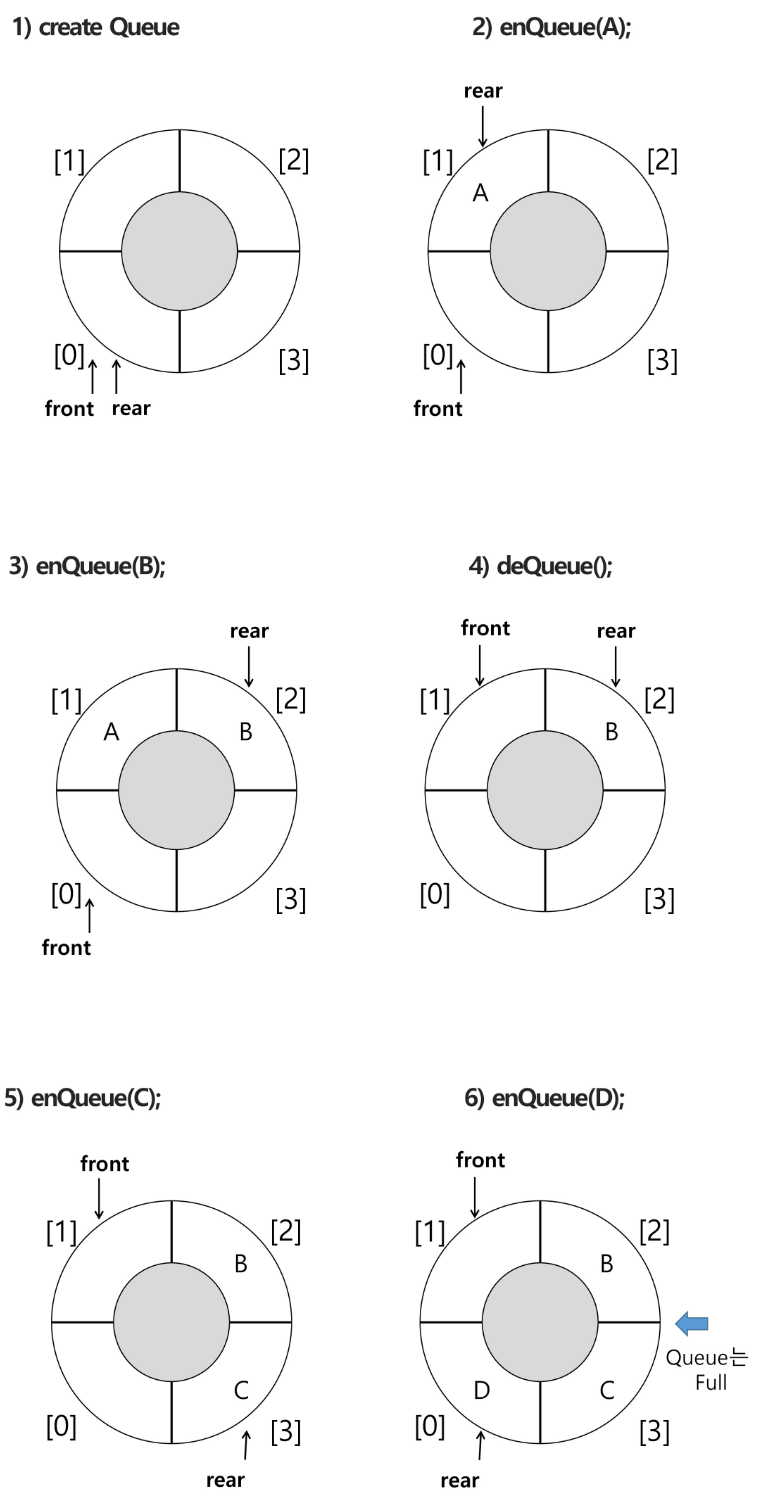
  • full 이라는 것은 6번과 같이 front가 있는 값은 0으로 둬야 한다. (삭제는 아닌, 그 값을 무시.)

---

코드 구현

1. 포화 상태 확인

static boolean isFull() {
	return (queue.length + front - rear) % queue.length == 0;
}

2. 공백 상태 확인

static boolean isEmpty() {
	return front == rear;
}

3. 삽입

static void enQueue(String data) {
	if (isFull()) {
		System.out.println("가득 찼습니다.");
		return;
	}

	rear = (rear + 1) % queue.length; // 1		
	queue[rear] = data;
}

• 순환을 위해서 인덱스를 올린 후 진행

4. 삭제

static String deQueue() {
	if (isEmpty()) {
		System.out.println("큐가 비어있습니다.");
		return null;
	}
		
	front = (front + 1) % queue.length;
	return queue[++front];
}

5. 조회

static String Qpeek() {
	if (isEmpty()) {
		System.out.println("큐가 비어있습니다.");
		return null;
	}
	return queue[(front + 1) % queue.length];
}

6. 데이터 갯수

static int size() {
	return (queue.length + rear - front) % queue.length;
}

• 선형 큐에서는 rear - front가 되었다.

---

---

우선순위 큐

• 우선 순위를 가진 항목들을 저장하는 큐
• FIFO 순서가 아니라, 우선 순위가 높은 순서대로 먼저 나가게 한다.
• 예시 : 시물레이션 시스템, 네트워크 트래픽 제어, 운영체제의 테스크 스케줄링

• 우선순위 큐의 구현

1. 배열을 이용한 우선순위 큐
2. 리스트를 이용한 우선순위 큐

• 우선순위 큐의 기본 연산

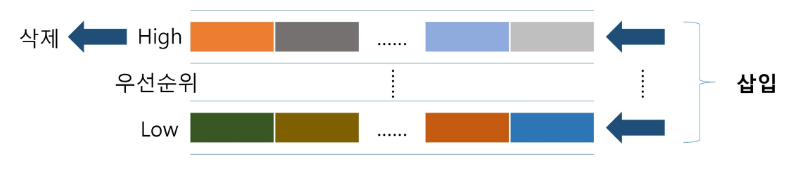
구현 순서

• 배열을 이용하여 자료 저장.
• 원소를 삽입하는 과정에서 우선순위를 비교하여 적절한 위치에 삽입하는 구조
• 가장 앞에 최고 우선 순위 원소가 위치하게 됨

문제점

• 시간, 메모리 낭비가 크다
  • 배열을 사용하게 되므로, 우선 순위에 따라 위치를 찾을 때 전부 탐색해야 한다.
  • 또한 삽입이나 삭제 연산이 일어날 때 원소의 재배치

---

---

삽입정렬

• 자료 배열의 모든 원소들을 앞에서부터 차례대로 이미 정렬된 부분과 비교
• 자신의 위치 찾아냄으로써 정렬을 완성 ( O($n^2$) 이 된다. )

정렬 과정

• 정렬할 자료를 두 개의 부분 집합 U, S로 가정

  • U : 정렬이 되지 않는 나머지 원소들
  • S : 정렬된 앞부분의 원소들

• 정렬되지 않은 U의 원소들을 하나씩 꺼내서, 정렬된 부분 S의 마지막 원소부터 비교하며 위치 찾아 삽입

• 삽입 정렬을 반복하며, S원소를 하나씩 늘리고 U의 원소는 하나씩 감소하게 한다.

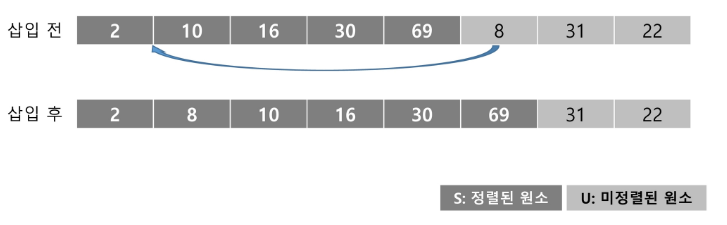
• 하나하나 비교하면서 뒤로 미뤄주기 때문에, 뒤부터 파악

• 그것보다 크면 값을 뒤로 하나씩 보내며 진행하면, 실행 시간이 줄어들게 된다.

• 또한, 운이 좋게 맨 뒤에 입력 가능한 값을 찾게 되면, 그 순간 입력만 하면 되기 때문에 뒤부터 확인

• 이미 정렬된 데이터가 많고, 새로 들어오는 데이터가 적을 때 유리하다.

---

코드 구현

1. 하나의 main 에서 실행

public class queue_원형큐3 {
	public static void main(String[] args) {
		int[] arr = {69, 10, 30, 2, 16, 8, 31, 22};
		
		// 삽입 정렬 
		// 첫 번째 값은 정렬의 기준이라 생각하고 진행하면 된다. 
		// i : 정렬되지 않은 집합의 첫번째 원소 
		for(int i = 1; i < arr.length; i++) {
			int data = arr[i];
			//비교 : 정렬된 집합의 뒤에서부터 비교하여 위치 찾아주기 
//			for(int j = i-1; j >= 0; j--) {
//				if(data < arr[j]) {
//					arr[j+1] = arr[j];
//					arr[j] = data;
//					System.out.println(Arrays.toString(arr));
//				} else {
//					break;
//				}
//			} 
			int j;
			for (j = i-1; j >=0 && arr[j] > data; j--) {
				arr[j+1] = arr[j];
			}
			arr[j+1] = data;
		}
		
		System.out.println(Arrays.toString(arr));
	}
	
}

2. 메소드로 분류하여서 진행

public class queue_원형큐2 {
	
	static int[] queue = new int[100];
	static int rear = -1;
	static int front = -1;
	
	public static void main(String[] args) {
		enQueue(10);
		enQueue(12);
		enQueue(3);
		enQueue(9);
		enQueue(8);
		
		System.out.println(deQueue()); // 3
		System.out.println(deQueue()); // 8
		System.out.println(deQueue()); // 9
		System.out.println(deQueue()); // 10
		System.out.println(deQueue()); // 12
	}
	
	static void enQueue(int data) {
		queue[++rear] = data;
		int i = rear;
		
		int j;
		for (j = i-1; j >=0 && queue[j] > data; j--) {
			queue[j+1] = queue[j];
		}
		queue[j+1] = data;
	}
	
	static int deQueue() {
		return queue[++front];
	}
	
	
}

---

---

정렬 특성 반복