분할 정복

분할 정복

• 큰 문제를 작은 하위 문제로 나누어 해결하는 방식

• 설계 전략
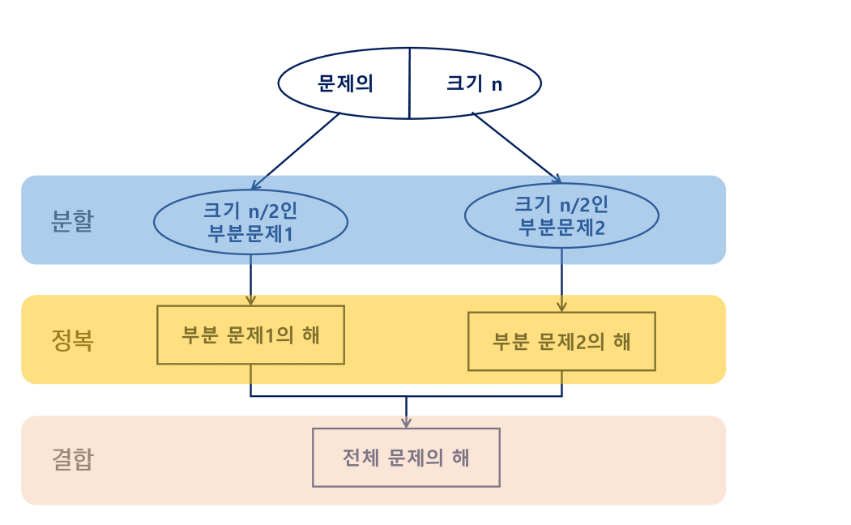
  • 분할 : 해결할 문제를 여러 개의 작은 부분으로 나눈다.
  • 정복 : 나눈 작은 문제를 각각 해결한다.
  • 결합 : 해결된 해답을 모은다.

• 자바 구현

public class cz_거듭제곱_분할정복 {
	public static void main(String[] args) {
		int C = 2;
		int N = 10;

	}

	public static int pow(int C, int N) {
		// 기저조건 (단, 0부터 시작하지 않는다는 조건에 한해서) 
		if(N == 1) return C;
		
		// 재귀부분 
		// 1. 짝수인 경우 
		if (N%2 == 0) {
			return pow(C, N/2) * pow(C, N/2);
		}
		// 2. 홀수인 경우
		else {
			return pow(C, (N-1)/2) * pow(C, (N-1)/2);
		}
		
		
	}
	
	// 상위 메소드는 pow를 반복해야 하므로, 동일한 값이기에 int에 저장하여 사용
	public static int pow2(int C, int N) {
		if(N == 1) return C;
		
		// 재귀부분 
		// 1. 짝수인 경우 
		if (N%2 == 0) {
			int tmp = pow2(C, N/2);
			return tmp * tmp;
		}
		// 2. 홀수인 경우
		else {
			int tmp = pow2(C, (N-1)/2);
			return tmp * tmp * C;
		}
	}
}

---

---

이진 검색

• 이미 정렬된 배열에서 특정한 값을 빠르게 찾기 위한 알고리즘
• 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함

• 검색 과정
  1. 중앙값 찾기
  2. 목표 값과 중앙 값 비교
     a. 목표 값과 중앙 값이 같은 경우 : 검색 종료
     b. 목표 값과 중앙 값이 작은 경우 : 왼쪽 절반 검색 수행
     c. 목표 값과 중앙 값이 큰 경우 : 오른쪽 절반 검색 수행
  3. 탐색 범위가 한 개의 원소가 될 때까지 반복 수행

• 자바 구현

public class cz_이진검색2 {

	static int[] arr = { 8, 9, 17, 21, 23, 35, 88, 369 };
	static int key;
	public static void main(String[] args) {
		// 우선 배열이 정렬되지 않았다면, 정렬 후 진행해야 한다.
		
		key = 35;
		
		System.out.println(binarySearch(0, arr.length-1));
		// Arrays.binarySearch 라는 메소드가 이미 지정되어 있다. 배열과 key 값을 입력하면 반환해준다.  
		
	}

	static boolean binarySearch(int left, int right) {
		// 기저 조건 
		// 잘못 입력이 되거나 교차가 될 때 false로 출력 
		if (left > right) return false;

		// 재귀 부분 
		int mid = (left+right)/2;
		
		// 1 같은 경우 
		if (arr[mid] == key) return true;
		
		// 2 작은 경우, 왼쪽 구간으로 탐색 
		else if (arr[mid] > key) return binarySearch(left, mid-1);
		
		// 3 큰 경우, 오른쪽 구간으로 탐색 
		else  return binarySearch(mid+1, right);

	}
}

• 시간 복잡도 : O(logN) → 1000개의 원소를 대략 10번의 비교로 찾을 수 있다.
• 데이터의 삽입, 삭제가 자주 일어나면 정렬이 필요하여 비효율적일 수 있다.
• 다만, 크기가 작은 배열에서는 크게 이점이 없을 수도 있다.

---

---

병합 정렬

• 분할 정복 기법을 활용한 안정적인 정렬 알고리즘
• 배열을 절반으로 분할하고 각 부분을 재귀적으로 정렬한 뒤, 정렬된 부분을 다시 병합하는 정렬 방식
• O(NlogN)
• 추가적인 공간이 별도로 필요하다.
• 이미 정렬이 되어 있는 두 개의 배열이 있다면, 이 둘을 합쳐서 정렬된 배열로 만드는 것은 매우 쉽다는 것이 핵심 아이디어이다.

• 단계별 동작
  • 분할 : 주어진 배열을 반으로 나눈다.
  • 정복 : 각 부분 배열을 재귀적으로 병합 정렬을 사용해 정렬한다.
  • 병합 : 정렬된 부분 배열들을 합쳐 전체 배열을 정렬한다.

• 예시

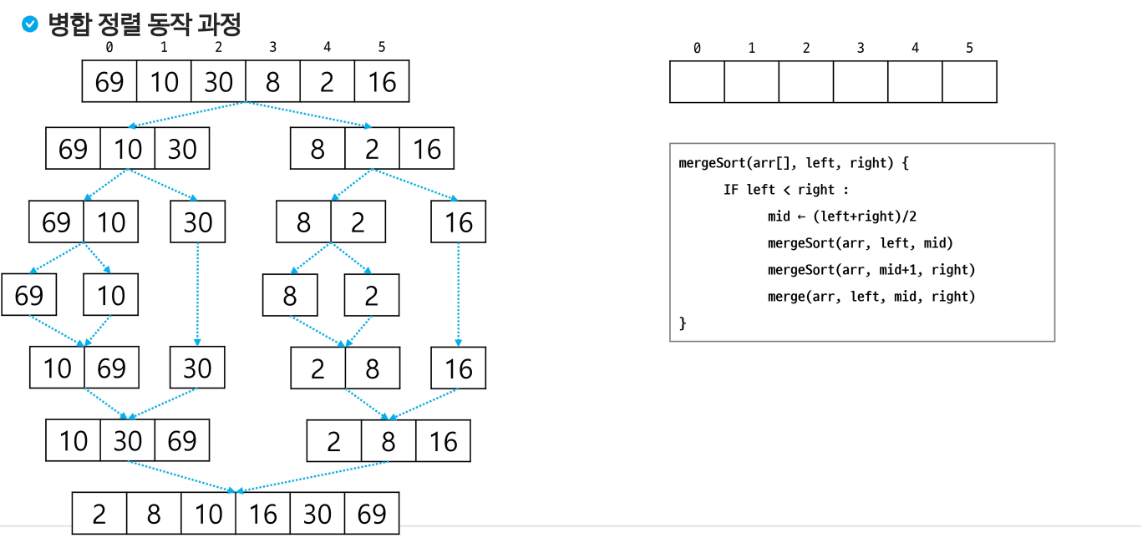
• 자바 구현

import java.util.Arrays;

public class cz_병합정렬 {
	static int[] arr = {7, 5, 13, 2, 79, 12, 35, 42};
	static int N = arr.length; // 배열의 길이 
	static int[] tmp = new int[N]; 
	
	public static void main(String[] args) {
		mergeSort(0, N-1);
		
		System.out.println(Arrays.toString(arr));
	}
	
	// 구간을 쪼개는 로직 
	static void mergeSort(int left, int right) {
		// left : 구간의 시작 위치 / right : 구간의 끝 위치 
		
		if (left < right) { // 아직 할 게 남아있다. 
			int mid = (left+right) / 2;
			mergeSort(left, mid);
			mergeSort(mid + 1, right);
            merge(left, mid, right);
		}
	}
	
	// 시작, 중앙(왼쪽 끝), 끝 부분에 대한 설명 
	static void merge(int left, int mid, int right) {
		int L = left;
		int R = mid + 1;
		
		int idx = left; // tmp(비어있는) 배열의 인덱스 
	
		while (L <= mid && R <= right) { // 아직 왼쪽과 오른쪽 구간이 끝에 닿지 않았을 경우에 
			if(arr[L] <= arr[R]) {
				tmp[idx++] = arr[L++];
			} else {
				tmp[idx++] = arr[R++];
			}
		}
		
		// 왼쪽 구간의 값이 남은 경우 
		if(L <= mid) {
			for(int i = L; i <= mid; L++) tmp[idx++] = arr[i];
		}
		
		// 오른쪽 구간의 값이 남은 경우
		else {
			for(int i = R; i <= right; L++) tmp[idx++] = arr[i];
		}
		
		// 원본 배열에 반영 
		for(int i = left; i <= right; i++) {
			arr[i] = tmp[i];
		}
	}
}

---

---

퀵 정렬

• 피벗이라는 기준 요소를 선택하여 배열을 두 부분으로 분할하고, 재귀적으로 정렬하는 방식
• O(NlogN), 최악에는 O(N2)
• 추가적인 공간을 필요치 않아 한다.
• 기준점을 옮기기 때문에, 배열에서 특정한 한 원소만 선택해서 이를 정렬된 위치에 놓는 것이 쉽다.

• 단계 별 동작
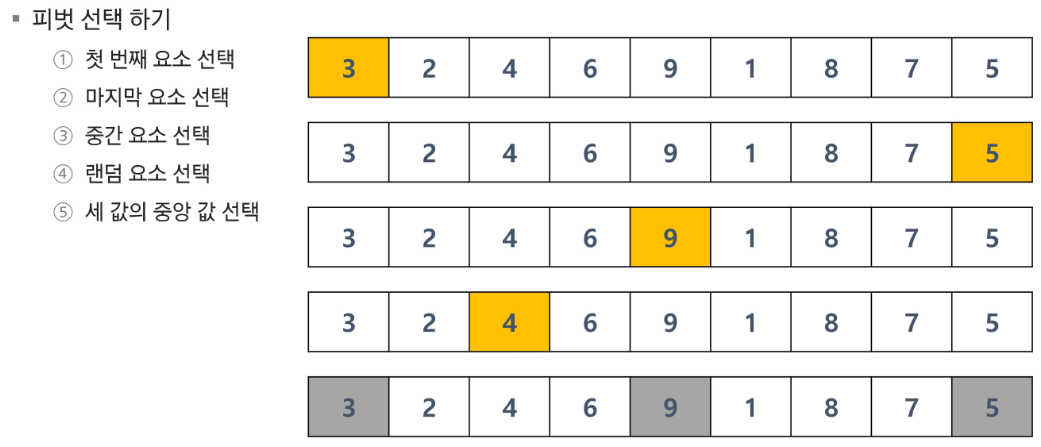
  1. pivot 결정
  2. 분할 : pivot보다 작은 요소는 왼쪽, 큰 요소는 오른 쪽에 위치
  3. 정복 : 분할된 배열을 다시 재귀적으로 정복한다.
  4. 병합

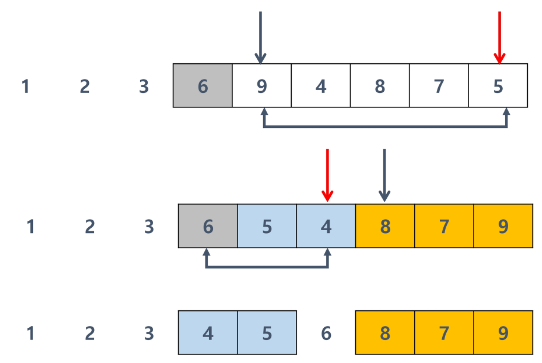
퀵 정렬 과정

Hoare 파티션

1. 만약 작은 값을 순서대로 정렬하는 경우
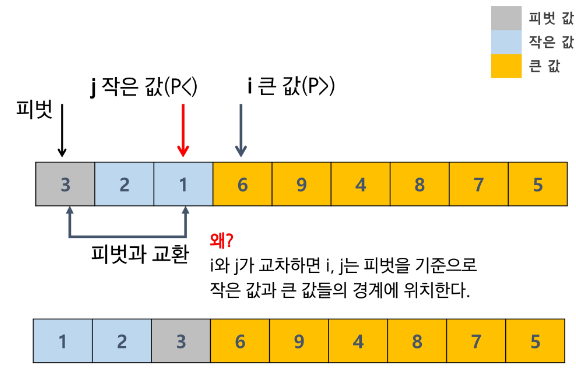
2. 3이 교환이 완료가 되면 그 다음 기준으로 정렬을 한다.

static void quickSort(int left, int right) {
	if (left < right) {
		int pivot = partition(left, right);
		quickSort(left, pivot - 1);
		quickSort(pivot + 1, right);
	}
}

// 반환값은 피봇의 위치
private static int partition(int left, int right) {
	int pivot = arr[left];

	int L = left + 1, R = right;

	while (L <= R) {
		// L : pivot 보다 큰 값을 찾을 때까지 이동을 하겠다.
		while (L <= R && arr[L] <= pivot)
			L++;
		// R : pivot 보다 작거나 같은 갑을 만날 때까지 이동을 하겠다.
		while (arr[R] > pivot)
			R--;

		if (L < R) {
			int tmp = arr[L];
			arr[L] = arr[R];
			arr[R] = tmp;
		}
	}
	// R의 위치는 사실 피봇이 가야할 위치이다.
	int tmp = arr[left];
	arr[left] = arr[R];
	arr[R] = tmp;

	return R; // 피봇의 위치
}

Lomuto 파티션

• 1개를 기점으로 작고 큰 값을 분류한 후에, 나머지를 정리

import java.util.Arrays;

public class cz_퀵정렬 {
	static int[] arr = {7, 5, 13, 2, 79, 12, 35, 42};
	static int N = arr.length; // 배열의 길이 
	
	public static void main(String[] args) {
		pSort(0, N-1);
		
		System.out.println(Arrays.toString(arr));
	}
	
	static void pSort(int left, int right) {
		if (left < right) {
			int pivot = partirion(left, right);
			pSort(left, pivot-1);
			pSort(pivot+1, right);
		}
	}

	static int partirion(int left, int right) {
		int pivot = arr[right];
		
		int i = left - 1; // 작은 값들의 경계 
		
		for(int j = left; j < right; j++) {
			if(arr[j] <= pivot) {
				i++;
				int tmp = arr[i];
				arr[i] = arr[j];
				arr[j] = tmp;
			}
		}
		
		int tmp = arr[i+1];
		arr[i+1] = arr[right];
		arr[right] = tmp;
		
		return i+1;
	}
}