재귀호출

• 자기 자신을 호출하여 순환 수행되는 것
• 함수 호출은 메모리 구조에서 스택을 사용한다. (이름만 같은 메서드)
• 기본 부분 : 재귀 호출에서 빠져 나가기 위한 조건
• 재귀 부분 : 자신을 호출하는 부분 (기본 부분으로 유도한다.)
• 재귀적 프로그램을 작성하는 것은, 반복 구조에 비해 간결하고 이해하기 쉽다.

public class stack_factorial {

	public static void main(String[] args) {
		System.out.println(calculator(10));
		System.out.println(factorial(10));
	}
	
	static int calculator(int N) {
		int result = 1;
		for (int i = 1; i <= N; i++) {
			result *= i;
		}
		
		return result;
	}
	
	static int factorial(int N) {
		// 재귀 함수의 경우, 기저 조건이 필요하다. 
		if (N-1 >= 0) return N * factorial (N-1);
		else return 1;
	}

}

• 중복 호출의 문제로, 시간이 오래 걸리기도 한다.

public class stack_fibonacci {
	public static void main(String[] args) {
		int result = fibonacci(540);
		System.out.println(result);
		
		int result2 = fibonacci1(540);
		System.out.println(result2);
	}
	
	static int fibonacci(int N) {
		if (N <= 1) return N;
		return fibonacci(N - 1) + fibonacci(N - 2);
	}
	static int fibonacci1(int N) {
		int[] arr = new int[N+1];
		arr[1] = 1;
		for(int i = 2; i <= N; i++) {
			arr[i] = arr[i-1] + arr[i-2];
		}
		return arr[N];
	}
	
	
}

아래의 메소드가 이해는 어려울 수 있지만, 실행 시간이 더욱 빠르다.
다만 중복 계산이 있어서 속도가 늦어지기도 한다.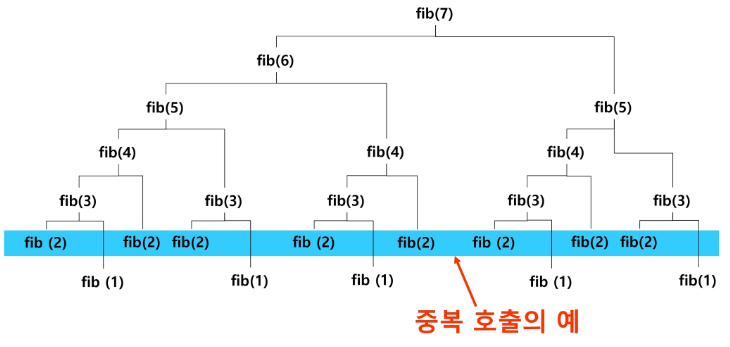

중복 값을 줄이기 위한 mFibo 사용

public class stack_fibonacci {
	public static void main(String[] args) {
		int result3 = mFibo(45);
		System.out.println(result3);
	}
    
	// Memoziation
	
	static int[] dp = new int[500];
	
	static { dp[1] = 1; }
	
	static int mFibo (int N) {
		if ( N <= 1) return N; // 보다 작은 경우, 그대로 리턴
		if (dp[N] != 0) return dp[N]; // 갑이 있다면 그대로 리턴 (계산 중복을 막기 위해)
		return dp[N] = mFibo(N - 1) + mFibo(N - 2); // 조건에 해당하지 않으면, 계산 후 출력 
	}
	
	
}