수치해석 @김현민, KMOOC

수치해석이란

수치해석 정의

• Numerical analysis is the study of algorithms for the problems of continuous mathematics - Lloyd N. Trefethen (1993)

Errors

• absolute error =|x-x*|
• relative error = |x-x*| / |x|

Sources of errors

• Mathematical modeling : simplifying, assumptions
• Programing error
• Errros in input : Uncertainty associated with measurements
• Floating point arithmetic

Scope of numerical analysis

• n 차원의 input data 를 받아 m 차원의 output data 를 출력하는 함수, 방정식 (선형, 비선형 , 미분, 편미분), 선형 연립 방정식 (행렬)의 값, 고유 값, 고유 벡터, decomposition

Nonlinear equation root finding

Bisection method

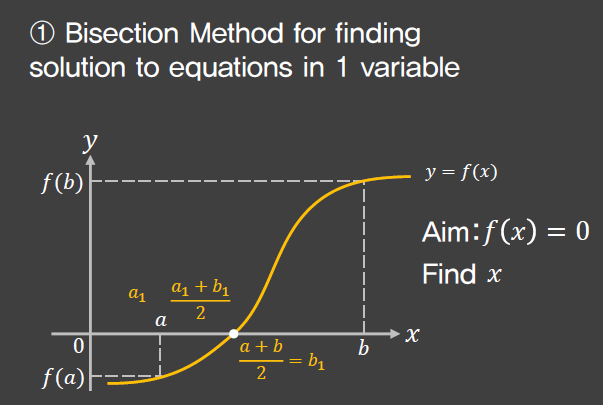
Fixed point iteration

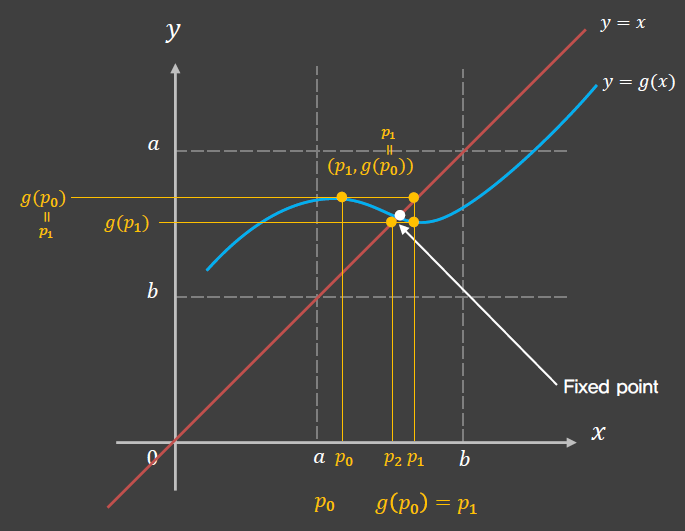
Newton's method

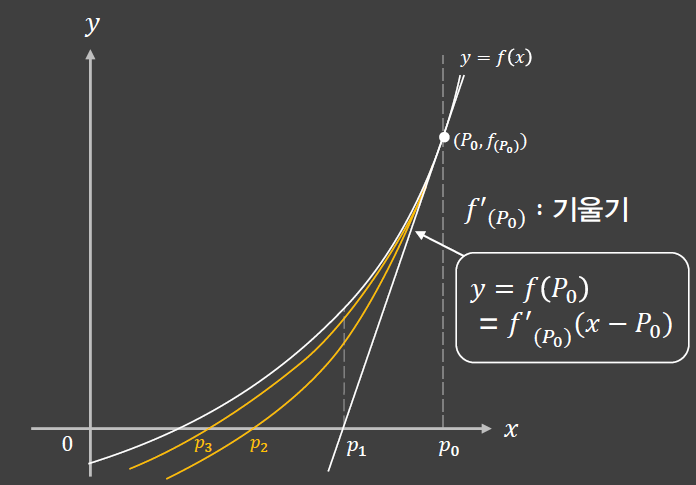
정리

• 위 3가지 방법 모두 각각 장,단점이 있음. Newton's method 는 한번 수렴하기 시작하면 수렴이 매우 빠름.

Error analysis

• 위 3가지 Root finding 수치해석 기법의 Error, iteration number 를 수학적으로 증명

Bisection method

Fixed point iteration

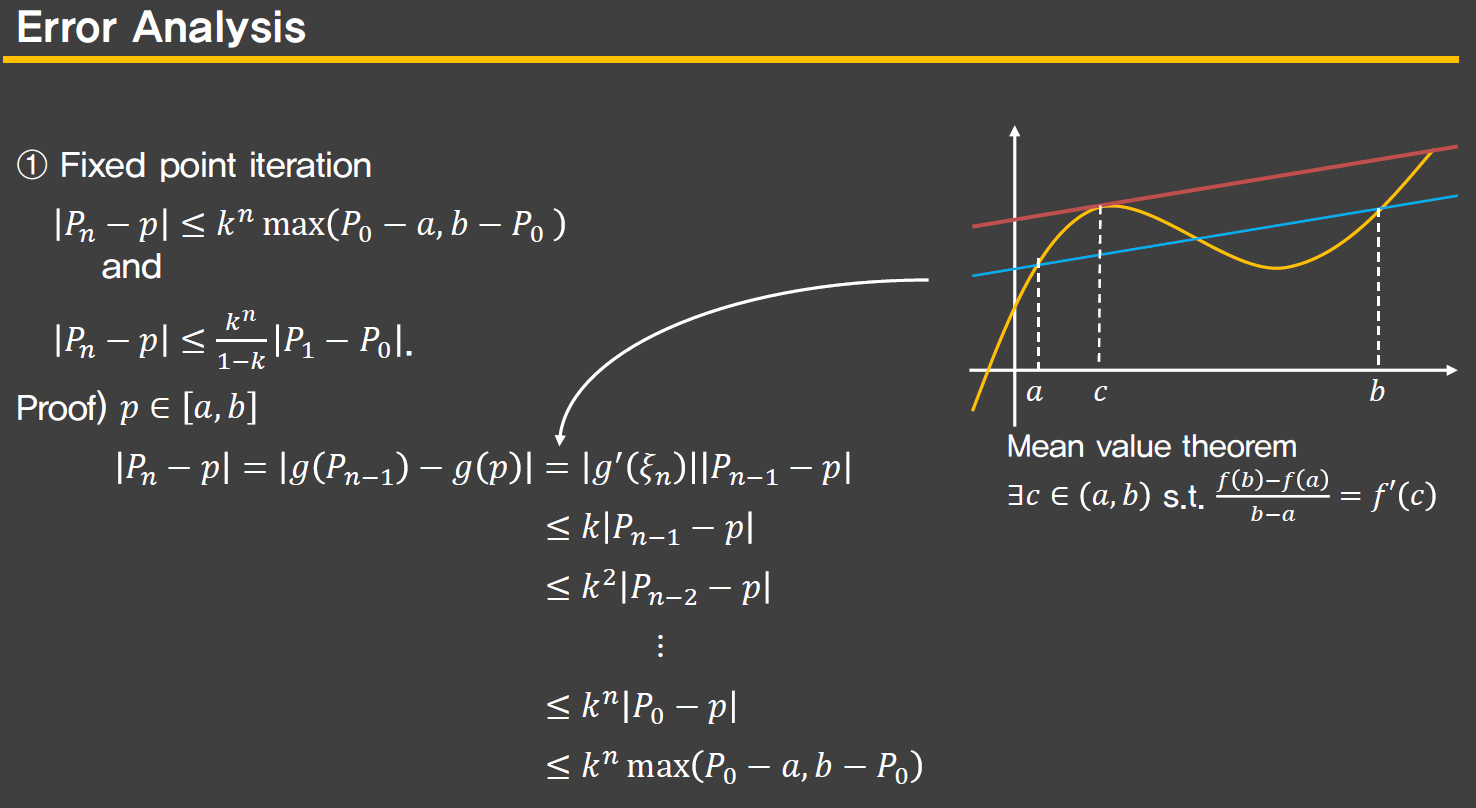
Newton's method

Interpolation, Spline

Lagrange polynomial

• Interpolation 방법 중 한가지로, 주어진 n+1개의 데이터 포인트를 정확하게 통과하는 n차 다항식을 구성하는 방법 중 하나
  

Divided difference

• Divided difference 의 장점으로는 real data 가 1개 추가 시, 항을 한번만 더 계산 하면 됨. (라그랑지 다항식의 경우 모든 계수를 모두 계산해야 함)
  
  

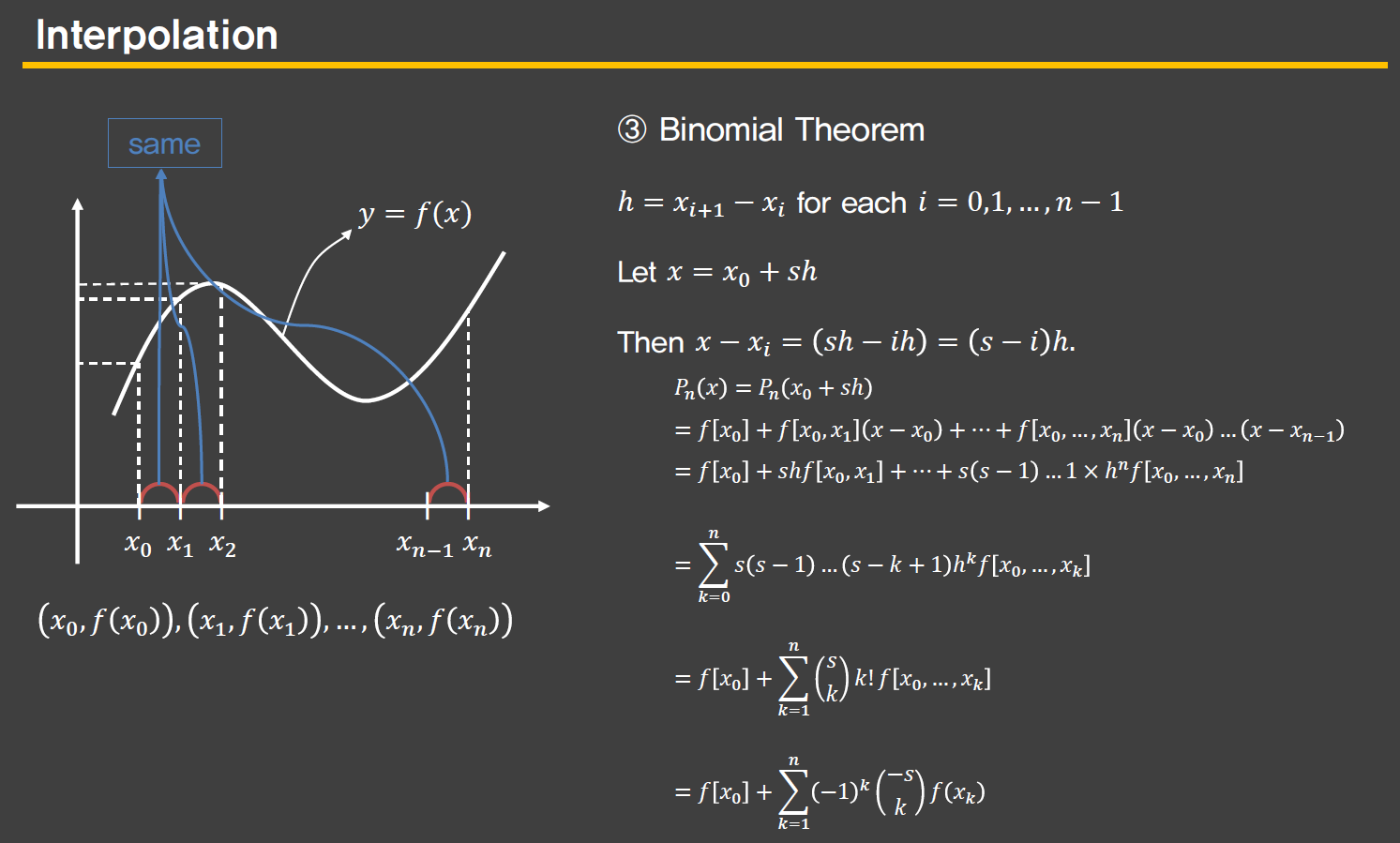
Binomial theorem

• real data 가 똑같은 간격으로 존재 할 때 (ex: x축이 time 인데, 동일 시간 간격으로 data 를 측정) 시, 적용 가능
• 좀 더 공부하기.. 일단 pass..
• 이 외에도 다양한 형태의 polynomial 을 통해서 interpolation 하는 방법들이 존재 함. 구글링하면 엄청나게 나옴.
  

Spline

• polynomial 과 같은 함수를 찾아서 interpolation 을 하는게 아니라, 인접한 data point 간 smooth 한 연결 (1차 다항식(linear), 2차 다항식(quadratic), 3차 다항식(cubic))을 통해서 interpolation 을 해보자
  

Numerical differentiation, integration

Newton Cotes formula

• 적분을 하려고 하는 f(x) 를 polynomial 로 approximation 한 다음 적분을 수행. 그런데 한번에 approximation 이 어려우므로, 구간을 쪼개서 수행.
  

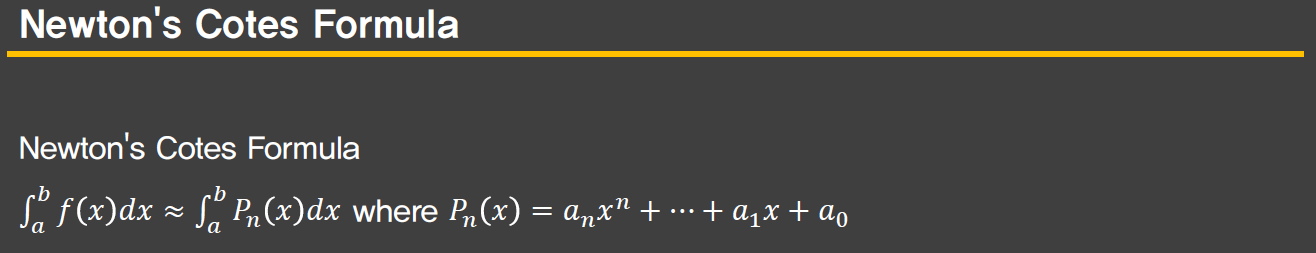
Simpson's rule

• n 개 점을 이어서 n-1 차 함수로 approximation 후 적분.
  

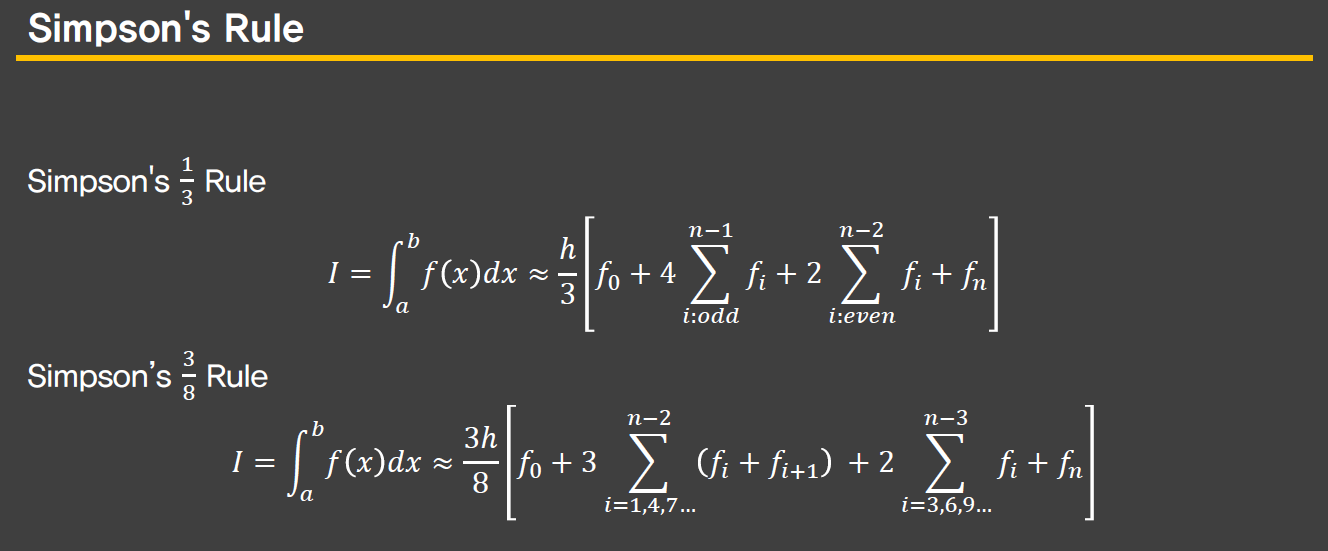
Linear algebra

Numerical solution idea

• 작은수로 나누는 것을 피해라! (유효숫자 한계..)
• 작은수로 나눠야 하면 최대한 뒤에서 해라! (처음에 하면 에러가 누적 됨..)
• 작다는 개념은 상대적으로 작은것도 포함된다!