Week2 Day2

📝 경사 하강법

📌 미분 (defferentiation)

• 변수의 움직임에 따른 함수 값의 변화를 측정하기 위한 도구 (최적화 기법)
• 미분은 함수 f의 주어진 점 (x, f(x))에서의 접선 기울기를 구한다.
• 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수 값이 증가하는지 / 감소하는지 알 수 있다.
  
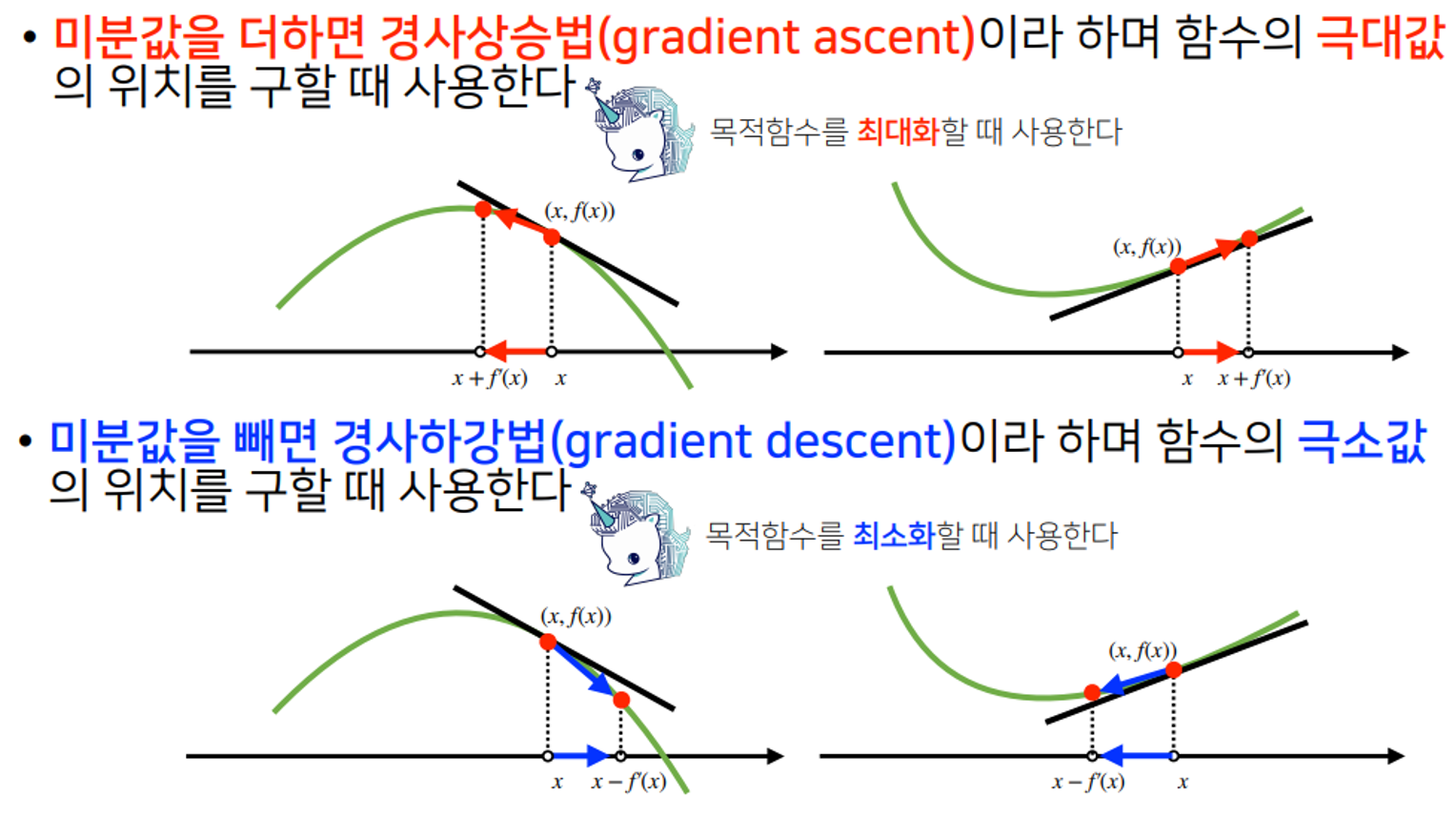
• 변수에 미분값을 더하면 경사 상승법
• 변수에 미분값을 빼면 경사 하강법

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val), fun

def func_gradient(fun, val):
    _, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff

def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5):
    cnt = 0
    val = init_point
    diff, _ = func_gradient(fun, init_point)
    while np.abs(diff) > epsilon:
        val = val - lr_rate * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
        
    print("함수: {}, 연산횟수: {}, 최소점: ({}, {})".format(fun(val)[1], cnt, val, fun(val)[0]))  
    
gradient_descent(fun= func, init_point=np.random.uniform(-2,2))

📌 선형 회귀 분석(역행렬)

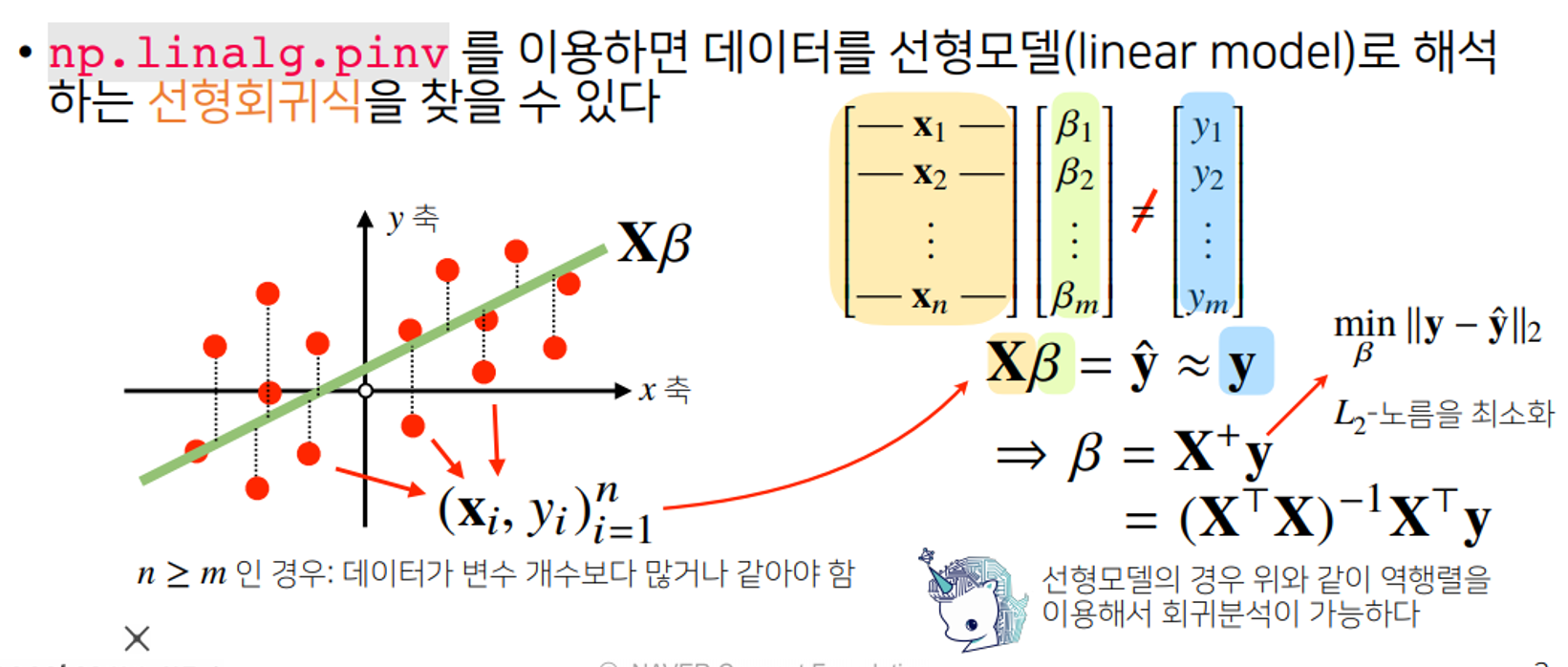
• 주어져있는 데이터와 가장 근사한 선형모델을 찾기 위해서
  L2 norm을 최소화 하는 계수찾기 위해서 무어펜로즈 역행렬이용
  

📌 선형 회귀 분석(경사하강법)

• 경사하강법을 이용해 적절한 선형모델을 찾아보자
  (선형모델이 아닌 다른 방식일 때도 일반적으로 사용 할 수 있다)
  
• 역행렬을 사용하지 않고도 최적화 할 수 있는 편리한 알고리즘
• 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장된다.

📌 확률적 경사하강법(SGD)

• 모든 데이터를 사용하여 업데이트하는 것이 아니라 데이터 하나, 일부만 사용하여 업데이트 한다.
  
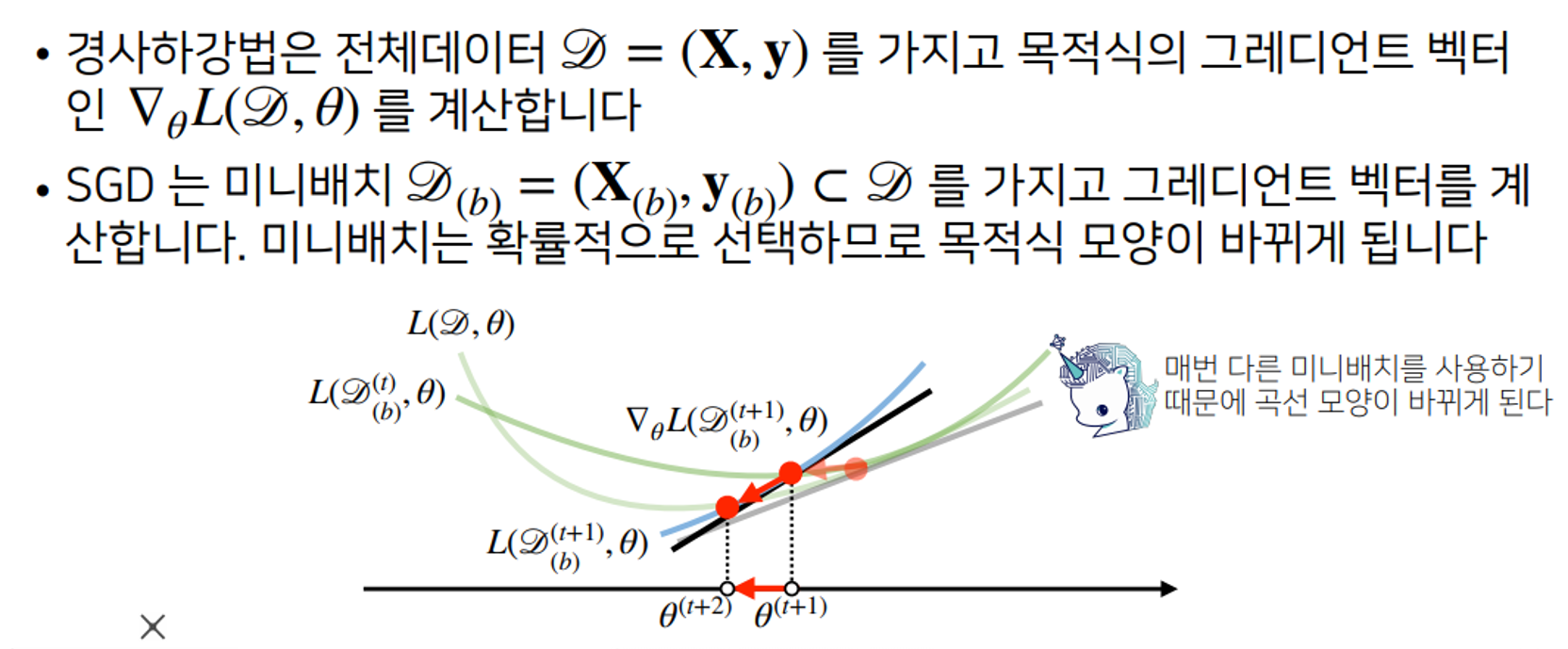
• 목적식이 볼록함수가 아닌경우 local minima가 존재할 수 있는데 SGD를 사용하면 이러한 극소지점에서 목적식이 확률적으로 바뀌면서 극소점을 더 이상 기울기 0이지 않게 하면서 탈출할 수 있도록 한다.
• 일반적 경사하강법 보다 효율적으로 연산한다.