Week3 Day1

📋 베이즈 통계학

📌 조건부 확률

• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려줍니다.
• $P(A\cap B)$ = $P(B)P(A|B)$
• $P(B|A)$ = $\frac{P(A\cap B)}{P(A)}$ = $P(B)$$\frac{P(A|B)}{P(A)}$

📌 베이즈 정리

• $P(\theta|D)$ = $P(\theta)$$\frac{P(D|\theta)}{P(D)}$
• $사후확률(posterior)$ = $사전확률(prior)$ $\frac{가능도(likelihood)}{Evidence}$
• $가능도(likelihood)$ : 현재 주어진 모수에서 이 데이터가 관측될 가능성
  $(Evidence)$ : 데이터 자체의 분포
  $사전확률(Prior)$ : 모수에 대한 확률 분포
  $사후확률(posterior)$ : 데이터를 관찰했을 때 이 파라미터가 성립할 확률
  
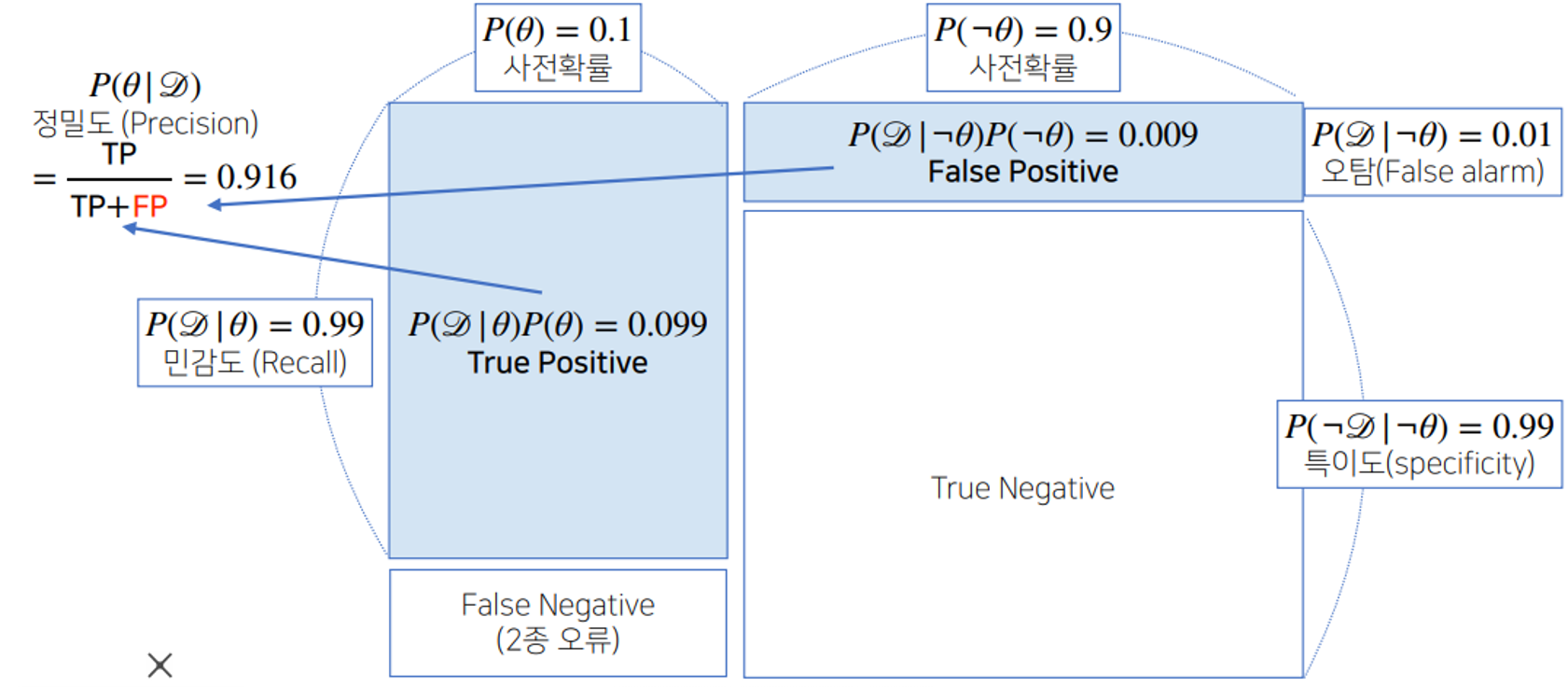
• 베이즈 정리를 통해서 새로운 데이터가 들어왔을 때 앞서 계산한 사후 확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.

📋 Neural Network & MLP

📌 Linear Neural Network

• Data / Model / Loss로 구성되어 있고 최적화 변수를 편미분 계산해 업데이트 해나간다.
• Matrix 연산(affine transform)을 통해서 두 벡터 space사이를 mapping해주는 역할을 한다.
• activation function을 통해서 Nonlinear transform

📌 Loss function

• 사용하는 loss function의 성질을 잘 파악하고 사용해야한다.
• L1-norm의 경우 L2-norm과 유사한 역할을 할 수 있다. L2-norm에 비해 이상치의 영향을 덜 받는 특징을 가지고 있다 그러나 0에서 미분이 불가능한 특징.
• Cross entropy loss는 분류문제에서 주로 사용되는데 일반적으로 분류문제에서 target은 one-hot vector로 표현된다. 이때 cross entropy loss를 최소화하는 것은 정답에 대한 logit값이 십만, 백만이 될 필요없고 해당하는 class의 상대적인 값만 높이겠다는 특징을 가지고 있다.
• Probabilistic Task의 경우 uncertainty 같은 정보를 활용할 수 있다.