Week3 Day2

📋 Optimization

📌 $Gradient$ $Descent$

$W_{t-1}$ <- $W_t$ - $\eta$ $g_t$

• $\eta$ : $Learning$ $rate$
• $g_t$ : $Gradient$
• $gradient$ 계산을 통해서 하강하는 방향으로 $weight$ $update$

📌 $Momentum$

$a_{t+1}$ <- $\beta$ $a_t$ + $g_t$
$W_{t+1}$ <- $W_t$ - $\eta$ $a_{t+1}$

• $a_{t+1}$ : $accumulation$
• $\beta$ : $momentum$
• 현재 스탭의 $accumulation$이용한 $momentum$ 과 현재 $gradient$ 를 함께 사용하여 다음 스탭의 $accumulation$
• $momentum$이 포함된 $gradient$를 이용한 $weight$ $update$
• 미니 배치를 사용하다 보니 그때 그때 세부적인 내용에 집중하게 되는데 이전에 사용한 미니배치의 $gradient$ 정보를 이용하여 문제 보완
• $Local$ $minima$에서 벗어날 수 있게해준다.

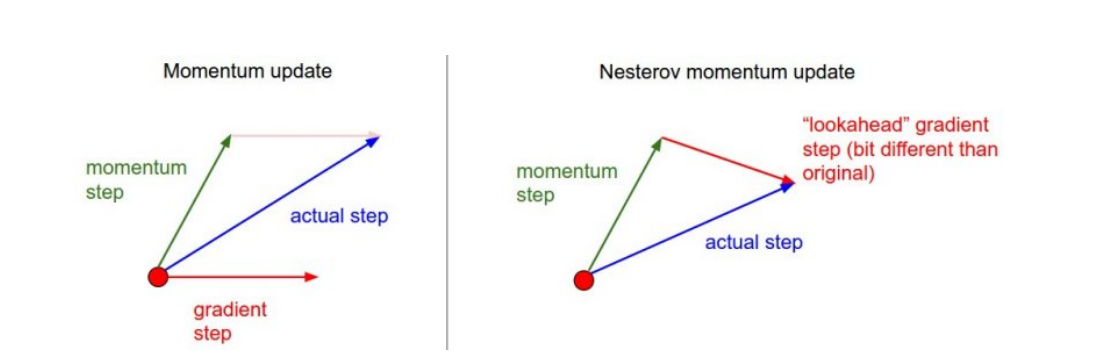
📌 $Nesterov$ $Accelerated$ $Gradient$

$a_{t+1}$ <- $\nabla$$\mathcal{L}$$(W_t -\eta \beta a_t)$
$W_{t+1}$ <- $W_t$ - $\eta$ $a_{t+1}$

• $\nabla$$\mathcal{L}$$(W_t -\eta \beta a_t)$ : $Lookahead$ $gradient$
• 현재 가지고 있는 $momentum$ 만큼 업데이트 했을 때를 미리 가보고 $gradient$를 구해서 모멘텀과 함께 $weight$ $update$에 사용한다.
  

📌 $Adagrad$

$W_{t+1}$ = $W_t$ - $\frac{\eta}{\sqrt{G_t + \epsilon}}$$g_t$

• $G_t$ : $Sum$ $of$ $gradient$ $squares$
• $\epsilon$ : $for$ $numeric$ $stability$
• $Sum$ $of$ $gradient$ $squares$ 를 통해서 지금까지 많이 변한 파라미터에 대해 적게 update, 적게 변한 파라미터에 대해 많이 업데이트
• 학습이 가면 갈 수 록 적게 학습되는 문제가 있을 수 있다.

📌 $Adam$

$m_t$ = $\beta_1$$m_{t=1}$ + $(1-\beta_1)$$g_t$
$v_t$ = $\beta_2$$v_{t-1}$ + $(1-\beta_2)$$g_t^2$
$W_{t+1}$ = $W_t$ - $\frac{\eta}{\sqrt{v_t + \epsilon}}$$\frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t}$$m_t$

• $m_t$ : $momentum$
• $v_t$ : $EMA$ $of$ $gradient$ $squares$
• $v_t$를 통해서 $gradient$ 크기 변화에 따라 $adaptive$ 하게 $learning$ $rate$ 바꿔주는 역할 + $m_t$ 를 통해서 이전의 $gradient$ 정보를 모멘텀으로 사용