Week5 Day1
📋
📌의 정의와 의미
- 그래프는 정점 집합과 간선 집합으로 이루어진 수학적 구조
- 그래프는 구성 요소 간의 복잡한 상호작용을 하는 복잡계를 표현하고 분석하기 위한 언어
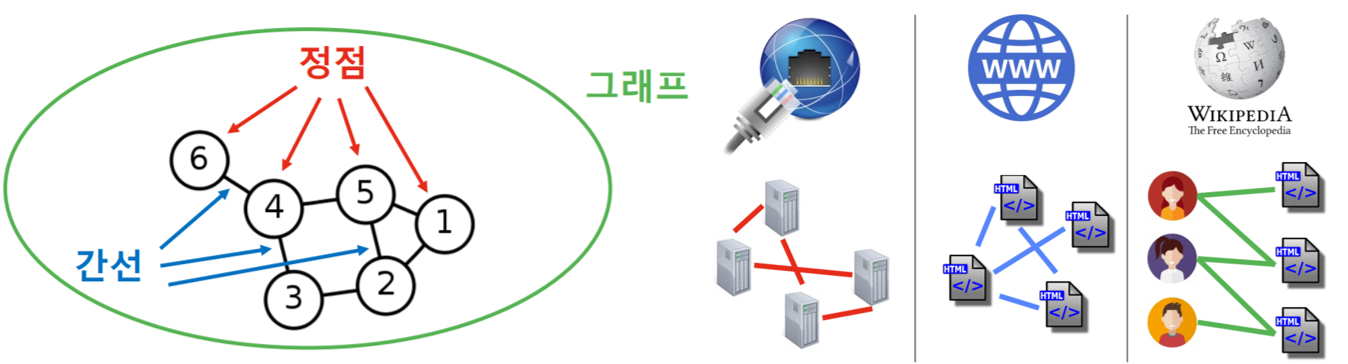
- 복잡계를 이해하고, 정확한 예측을 하기 위해서 복잡계 이면에 있는 그래프에 대한 이해가 필요하다.
📌 관련 인공지능 문제
- 정점 분류 문제
-> 그래프의 일부 노드의 레이블이 있는 상황에서 노드의 레이블을 분류하는 문제 - 연결 예측 문제
-> 그래프의 노드들 사이의 관계를 파악하고 노드 사이의 연관성을 예측하는 문제
ex) 영화와 유저가 노드라고 생각하고 유저가 영화를 봤을 때 간선이 연결된다고 할때 유저와 영화 쌍이 연결될 가능성을 예측 - 추천 시스템 문제
-> 유저의 선호도 및 과거 행동을 바탕으로 개인에 맞는 관심사를 제공하는 문제 - 군집 분석 문제
-> 실제 의미, 특성을 가지고 있는 연결 밀도가 높은 집단을 찾아내는 문제 - 랭킹 및 정보 검색 문제
-> 가장 중요한, 의미를 가진 노드를 찾아내는 문제 - 정보 전파 및 바이럴 마케팅 문제
-> 정보 전달을 최대화 할수 있는 노드를 찾는 문제
📌 유형 및 분류
- 방향이 없는 그래프 vs 방향이 있는 그래프
- 주체와 대상이 분리되었는지 그렇지 않은지에 따라
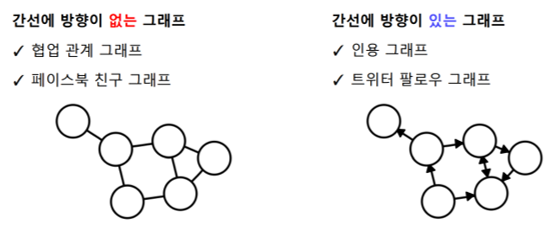
- 가중치가 없는 그래프 vs 가중치가 있는 그래프
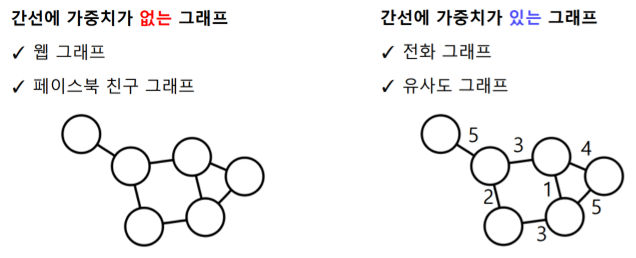
- 동종 그래프 vs 이종 그래프
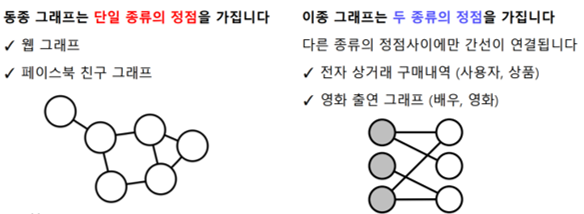
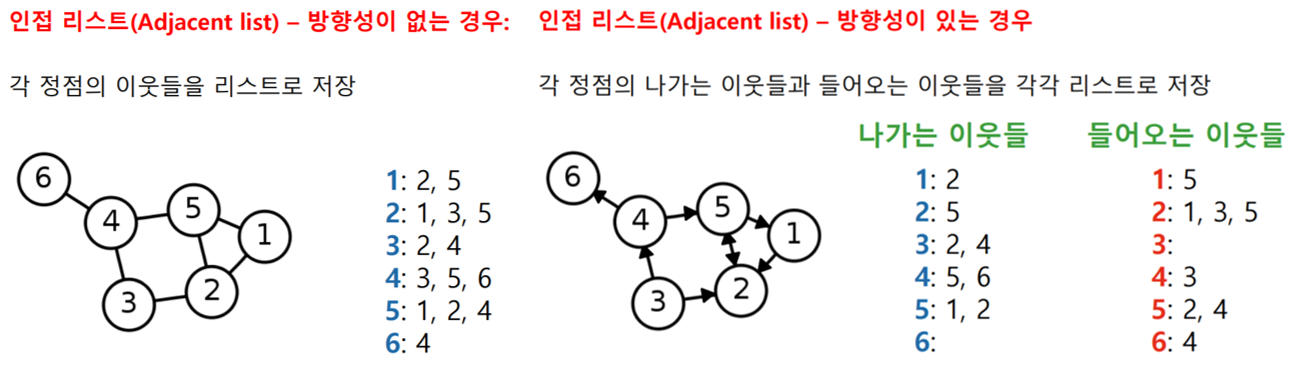
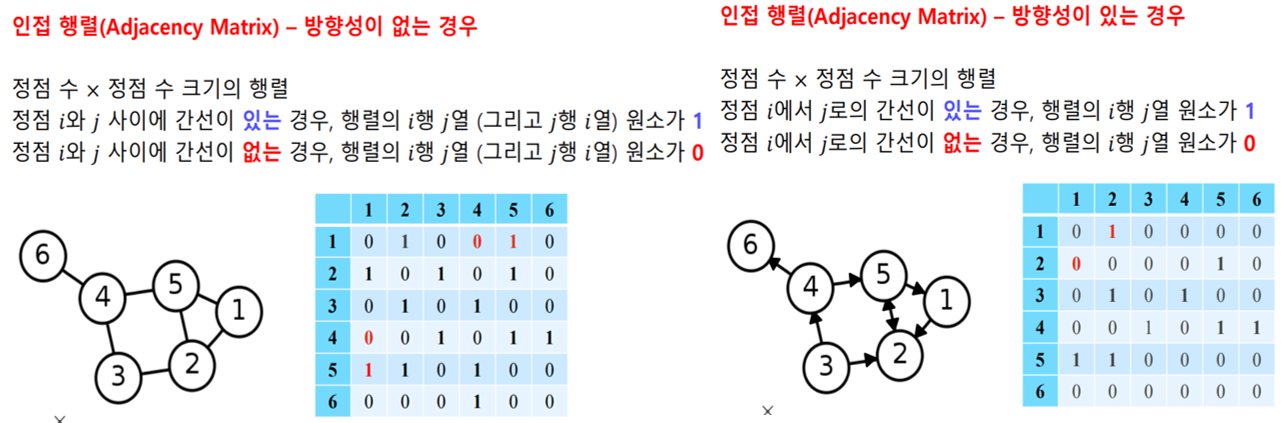
📌의 표현 및 저장
- 간선 리스트 : 그래프를 간선들의 리스트로 저장
📋 실제&랜덤 의 구조적 특징
📌 필수 개념
- 경로: 두 정점 , 사이의 경로는 조건을 만족하는 정점 순열
(1) 에서 시작해서 에서 끝나야 한다
(2) 순열에서 연속된 정점은 간선으로 연결되어 있어야 한다. - 거리: 정점 , 사이의 거리는 , 사이의 최단 경로 길이
- 지름: 그래프내 모든 정점 간 거리중 최댓값
📌 작은 세상 효과
- 많은 노드를 가지는 아주 큰 그래프여도 어떤 두 정점 사이의 거리는 그리 크지 않다.
- 이런 효과는 랜덤 그래프에도 존재한다.
- 하지만 체인, 사이클, 격자 그래프에서는 작은 세상 효과가 존재하지 않는다.
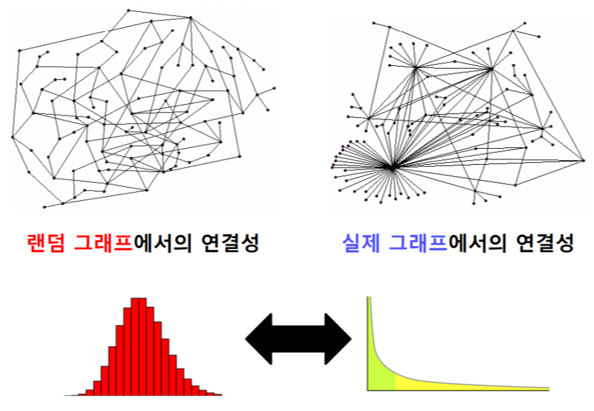
📌 연결성의 두터운 꼬리 분포
- 정점의 연결성는 그 정점과 연결된 간선의 수를 의미한다.
- 실제 그래프의 연결성 분포는 두터운 꼬리 분포를 가진다.
(연결성이 높은 허브 정점이 존재) - 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포
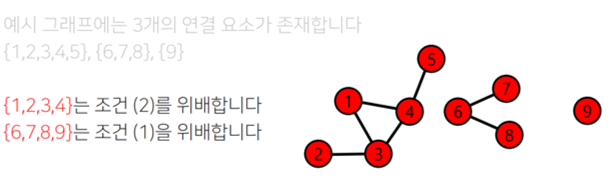
📌 거대 연결 요소
-
연결요소
(1) 연결 요소에 속하는 정점들은 경로로 연결 될 수 있다.
(2) 여전히 (1)의 조건을 만족하면서 추가 할 수 있는 더 이상의 정점이 존재하면 안된다.
-
실제 그래프에는 거대 연결 요소가 존재한다.
-
랜덤 그래프에도 높은 확률로 거대 연결 요소가 존재한다.

📌 군집 구조 -
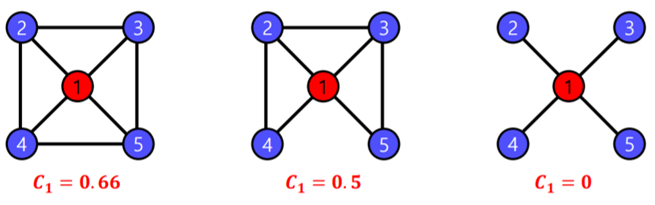
지역적 군집 계수: 정점 의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 의미한다.
-
지역적 군집 계수가 높다면 해당 정점과 그 이웃들은 높은 확률로 군집을 형성 시킨다.
-
전역 군집 계수: 각 정점에서의 지역적 군집 계수의 평균
-
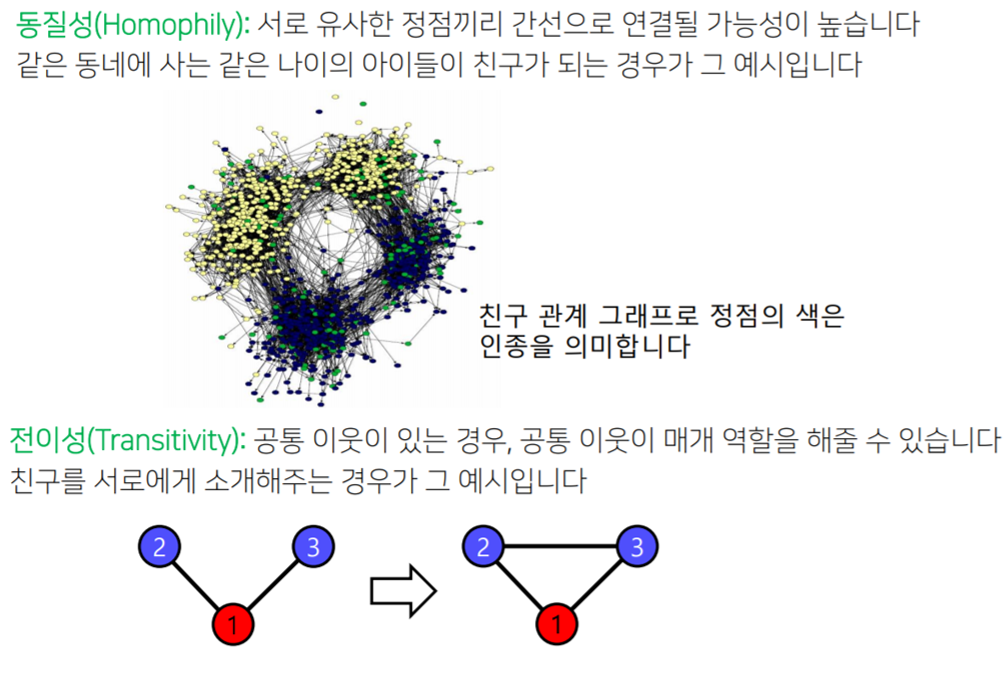
실제 그래프에서는 군집 계수가 높다. 즉 많은 군집이 존재한다.
-
반면 랜덤 그래프에서는 지역적 혹은 전역 군집 계수가 높지 않다.