컴퓨터 산술과 논리 연산

심영민·2023년 11월 26일
컴퓨터 구조
0

컴퓨터 구조

목록 보기
4/5
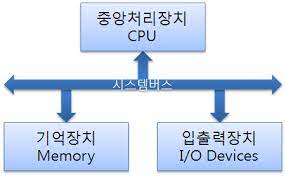
post-thumbnail

컴퓨터는 기본적으로 산술적 계산과 논리 데이터에 대한 연산을 한다.

ALU

기능

ALU는 CPU의 구성요소 중 하나로 컴퓨터 시스템의 다른 요소(제어 유니트, 레지스터, 주기억장치, I/O장치)는 ALU가 처리하는 데이터를 가져오고 결과 저장 및 출력을 한다.

ALU는 산술 연산 (+, -, x, ÷)을 수행하고, 논리 연산 (AND, OR, XOR, NOT)을 수행한다.

구성 요소

  • 산술 연산장치 : 산술 연산을 수행
  • 논리 연산장치 : 논리 연산을 수행
  • 쉬프트 레지스터 : 비트들을 좌측 혹은 우측으로 이동시키는 기능을 가진 레지스터
  • 보수기 : 2진 데이터를 2의 보수로 변환(음수화)
  • 상태 레지스터 : 연산 결과의 상태를 나타내는 플래그들을 저장하는 레지스터

동작

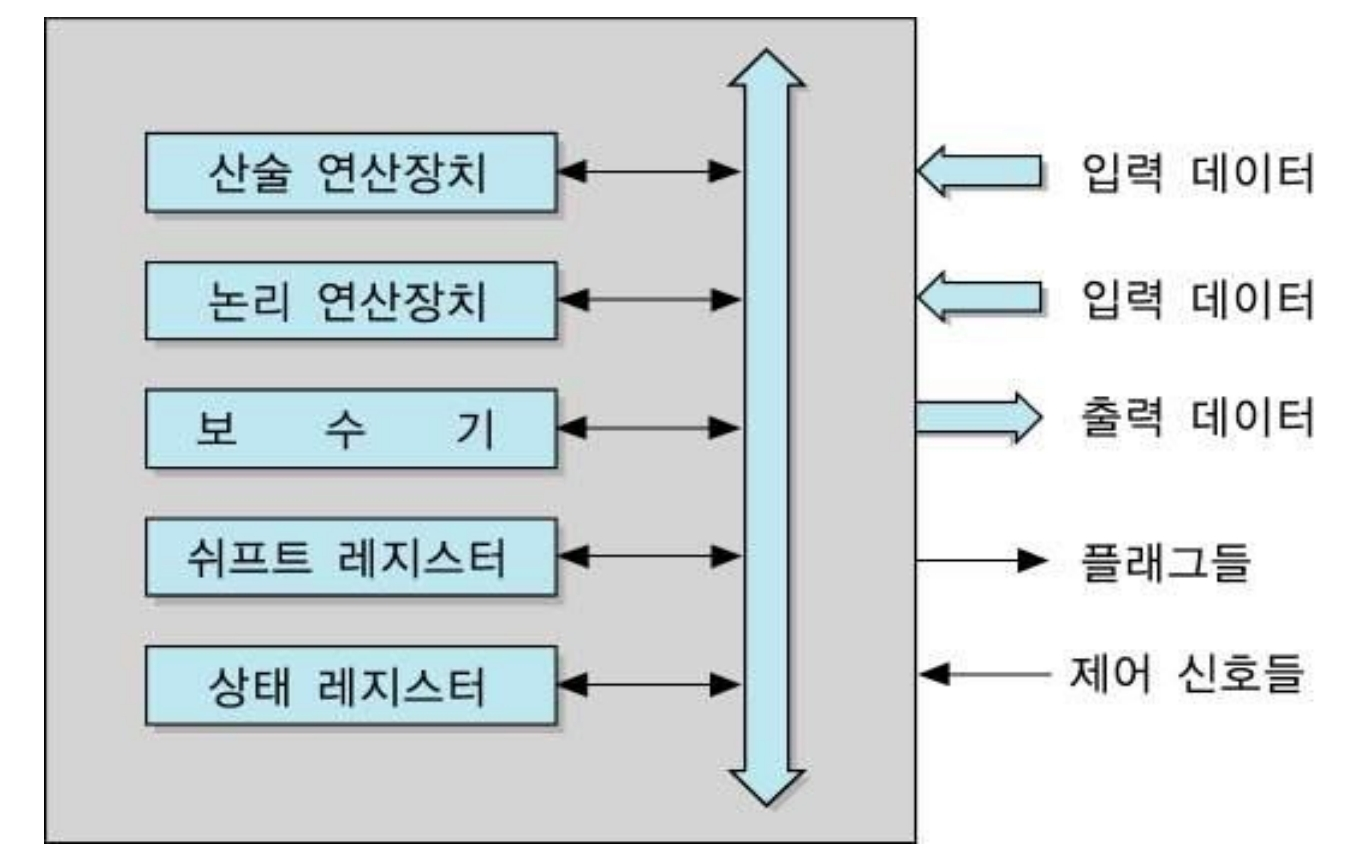
ALU는 레지스터 및 주기억 장치에서 데이터를 입력받아 처리하고, 다시 레지스터로 데이터를 보내 저장한다.
상태 레지스터에서는 ALU 연산의 결과에 따라 상태 레지스터의 플래그 값을 세트한다.
ALU 외부에 있는 제어유니트에서는 입력 데이터에 대한 연산을 수행할 내부 요소를 선택하고 ALU 내외로 데이터 이동 제어신호를 발생한다.

정수의 표현

2진수는 0,1,부호, 소수점으로 표현한다.
컴퓨터는 부호, 소수점을 사용안하고 0과1로만 표현한다.

10진수를 2진수로 변환하는 법은 아래와 같이 2로 나눠주면된다.

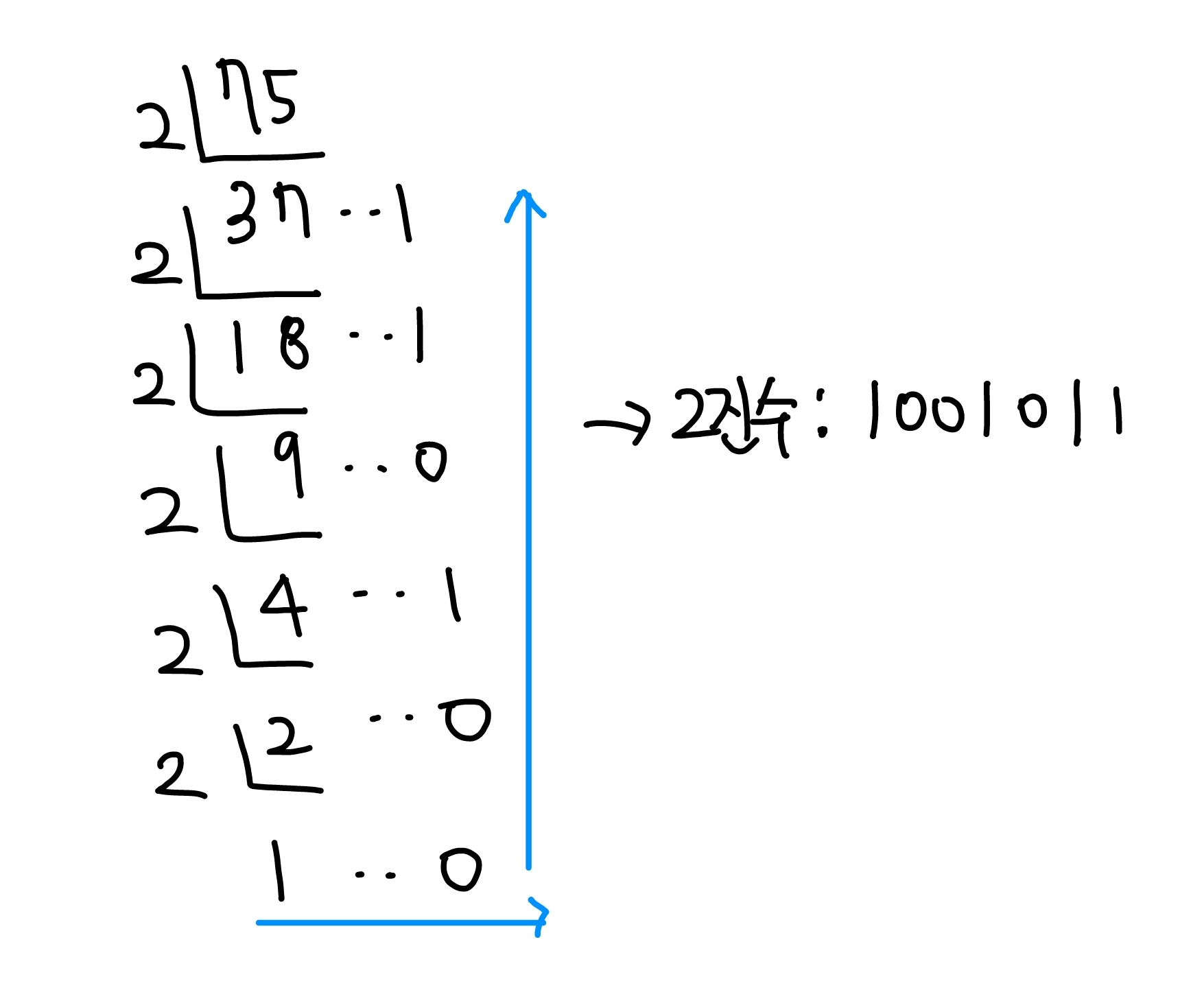
소수의 경우는 아래와 같이 2를 곱해주면된다.

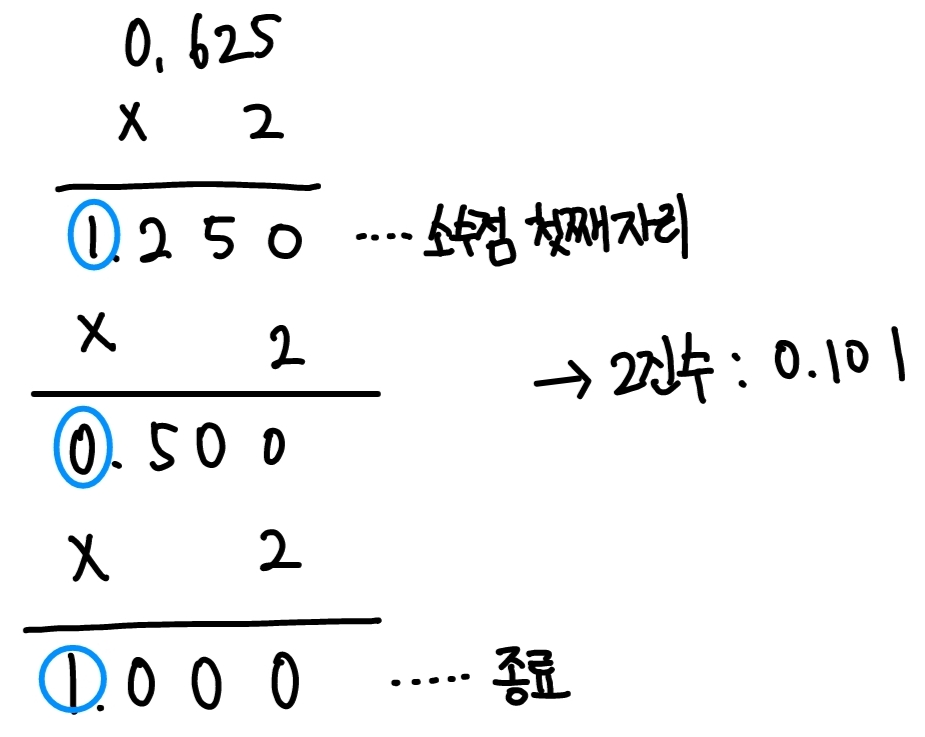
반대로 2진수를 10진수로 변환하는 법은 아래와 같이 2진수의 제곱근을 각각 곱해주면 된다.

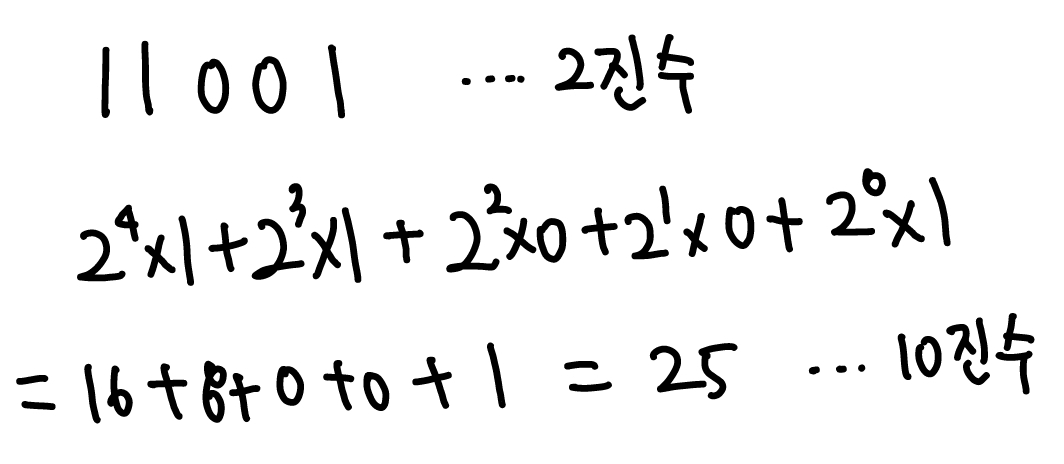
음수 표현

음수 표현 방법은 아래와 같이 3가지 방식이 있다.

부호크기 표현

부호 크기 표현은 맨 좌측 비트로 부호를 표현하고 나머지 N-1개의 비트는 크기를 표현한다.
+9를 부호크기 표현으로 나타내면 0 0001001이고
-9를 부호크기 표현으로 나타내면 1 0001001이다.

하지만 덧셈과 뺄셈을 수행하기 위해서는 부호비트와 크기 부분을 별도로 처리해야한다는 단점이 있고, 0을 표현할때 0 0000000과 1 0000000 로 2가지 표현 방식이 존재한다는 단점이 있다.

1의 보수 표현

1의 보수 표현은 모든 비트들을 반전시켜 표현하는 방식이다. (0->1, 1->0)
1의 보수 표현도 0이 2가지의 표현 방식이 존재한다는 단점이 있다.

2의 보수 표현

2의 보수 표현은 1의 보수 표현과 같이 모든 비트들은 반전시킨 후에 결과값에 1을 더하는 방식이다.

  • +9 = 0 0001001
  • -9 = 1 1110110 -> 1의 보수
  • -9 = 1 1110111 -> 2의 보수

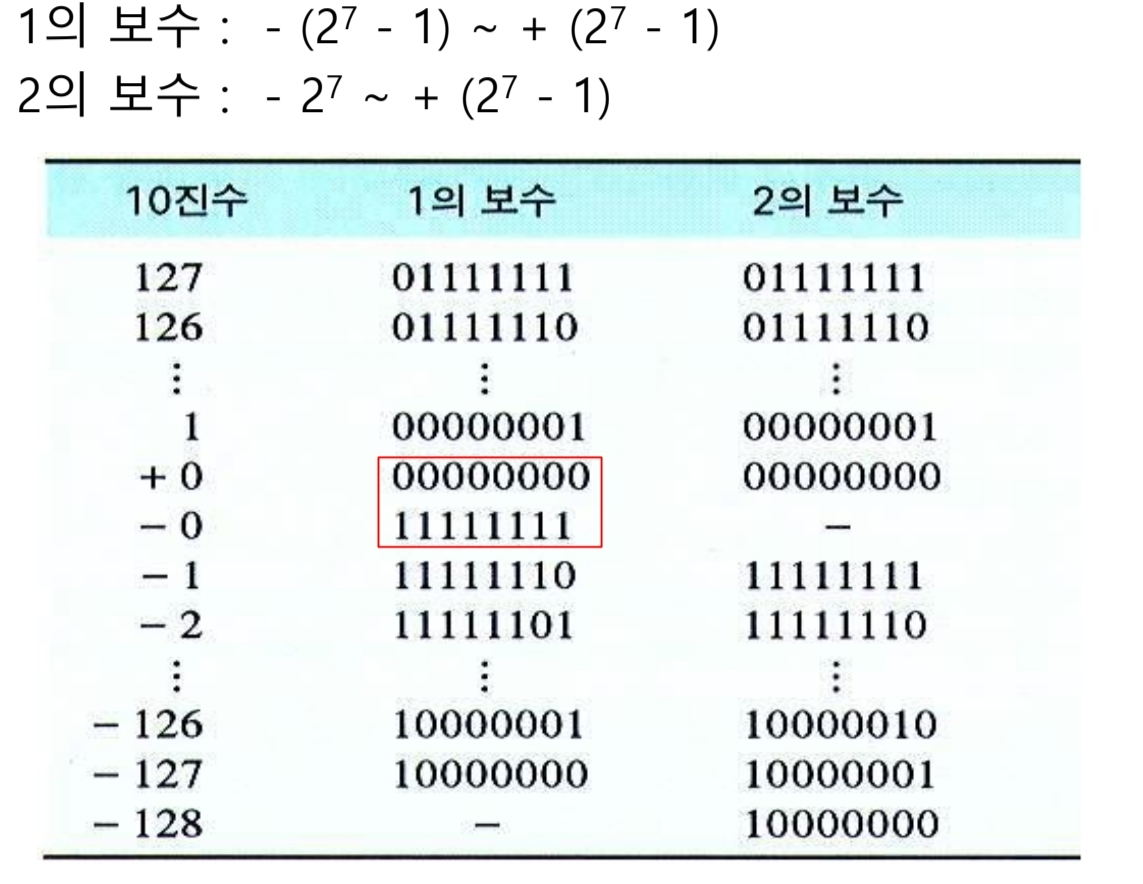
1의 보수와 2의 보수의 2진수로 표현할 수 있는 10진수의 범위

논리 연산

수를 나타내는 데이터는 단어 단위로 취급하고, 논리 데이터는 각 비트 단위로 취급한다.
기본적인 논리 연산은 아래와 같다.

A BNOT ANOT BA AND BA OR BA XOR B
0 011000
0 110011
1 001011
1 100110

데이터를 변경하기 위한 논리 연산

A와 B의 레지스터가 각각 다음과 같을 때 아래와 같은 연산을 통해 데이터를 변경한다.

선택적-세트 연산

OR 연산을 사용하여 데이터를 변경한다.

A = 1001 0010
B = 0000 1111
-------------
A = 1001 1111

선택적-보수 연산

XOR 연산을 이용하여 데이터를 변경한다.

A = 1001 0101
B = 0000 1111
-------------
A = 1001 1010

마스크 연산

AND 연산을 이용하여 데이터를 변경한다.
(단어내의 원하는 비트를 선택적으로 clear하는데 사용됨)

A = 1101 0101
B = 0000 1111
-------------
A = 0000 0101

삽입 연산

삽입될 비트 위치들에 대해 마스크 연산을 수행후
새로 삽입할 비트들과 OR 연산을 수행한다.

A = 1001 0101
B = 0000 1111  [AND 연산]
-------------
A = 0000 0101
B = 1110 0000  [새로 삽입할 비트와 OR 연산]
-------------
A = 1110 0101

비교 연산

A와 B레지스터의 내용을 비교하는 연산으로 XOR 연산 수행하고 결과는 A레지스터에 저장한다.

A = 1101 0101
B = 1001 0110
-------------
A = 0100 0011

쉬프트(shift)연산

논리적 쉬프트란 레지스터내의 데이터 비트들을 왼쪽 혹은 오른쪽으로 한 칸씩 이동하는 것을 말한다.
좌측 쉬프트는 비트들이 좌측으로 한 칸씩 이동하는 것으로 최하위 비트 A1은 0, 최상위 비트 A4는 버린다.
우측 쉬프트는 비트들이 우측으로 한 칸씩 이동하는 것으로 최상위 비트 A4는 0, 최하위 비트 A1는 버린다.

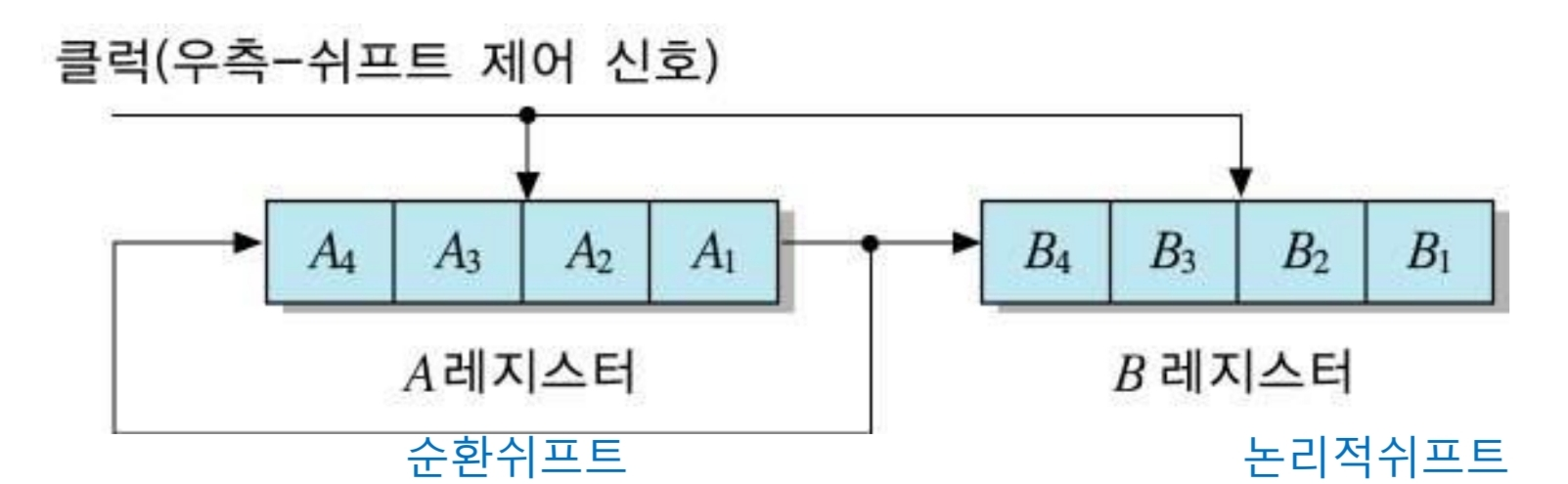
쉬프트 레지스터

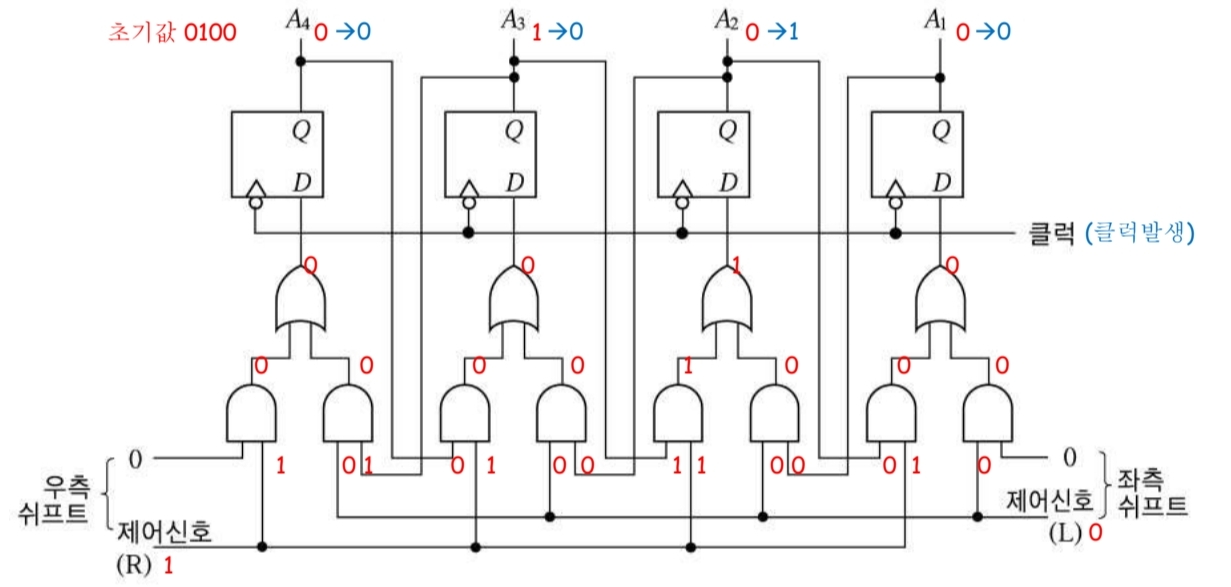
위 그림은 D-플립플롭을 이용한 쉬프트 연산 기능 레지스터이다.
클럭이 발생하면 입력이 출력으로 전달되고 우측 쉬프트 동작을 거친다.

쉬프트 종류

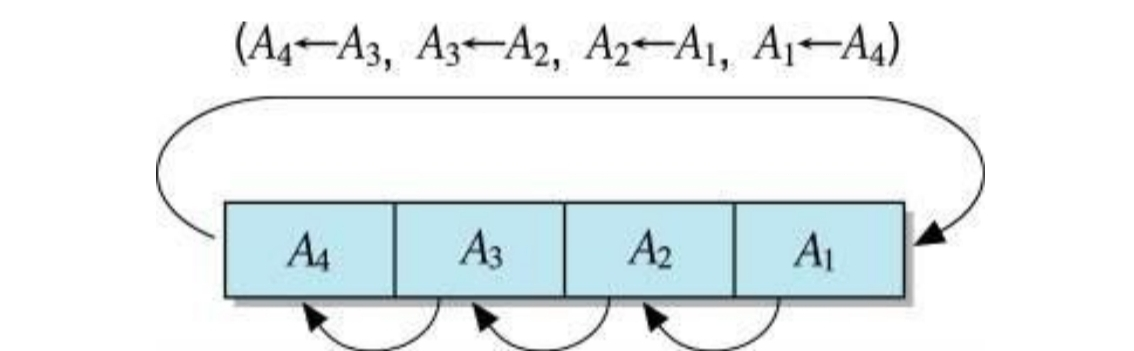
순환 쉬프트

순환 쉬프트는 최상위 혹은 최하위 비트를 버리지 않고 순환시킨다.

산술적 쉬프트

수를 나타내는 데이터에 대한 쉬프트로 부호 비트는 유지하고 크기 비트들만 쉬프트한다.

직렬 데이터 전송

쉬프트 연산을 데이터 비트 수만큼 연속적으로 수행하여 두 레지스터들 사이에 한 개의 선을 통하여 전체 데이터를 이동하는 동작이다.

정수의 산술 연산

덧셈

기본적으로 2의 보수로 표현된 수들의 덧셈은 올림수를 버리는 방식을 사용한다.

(-3) + (+3) = 0

 1101
+0011
------
 0000  = 0

병렬 가산기

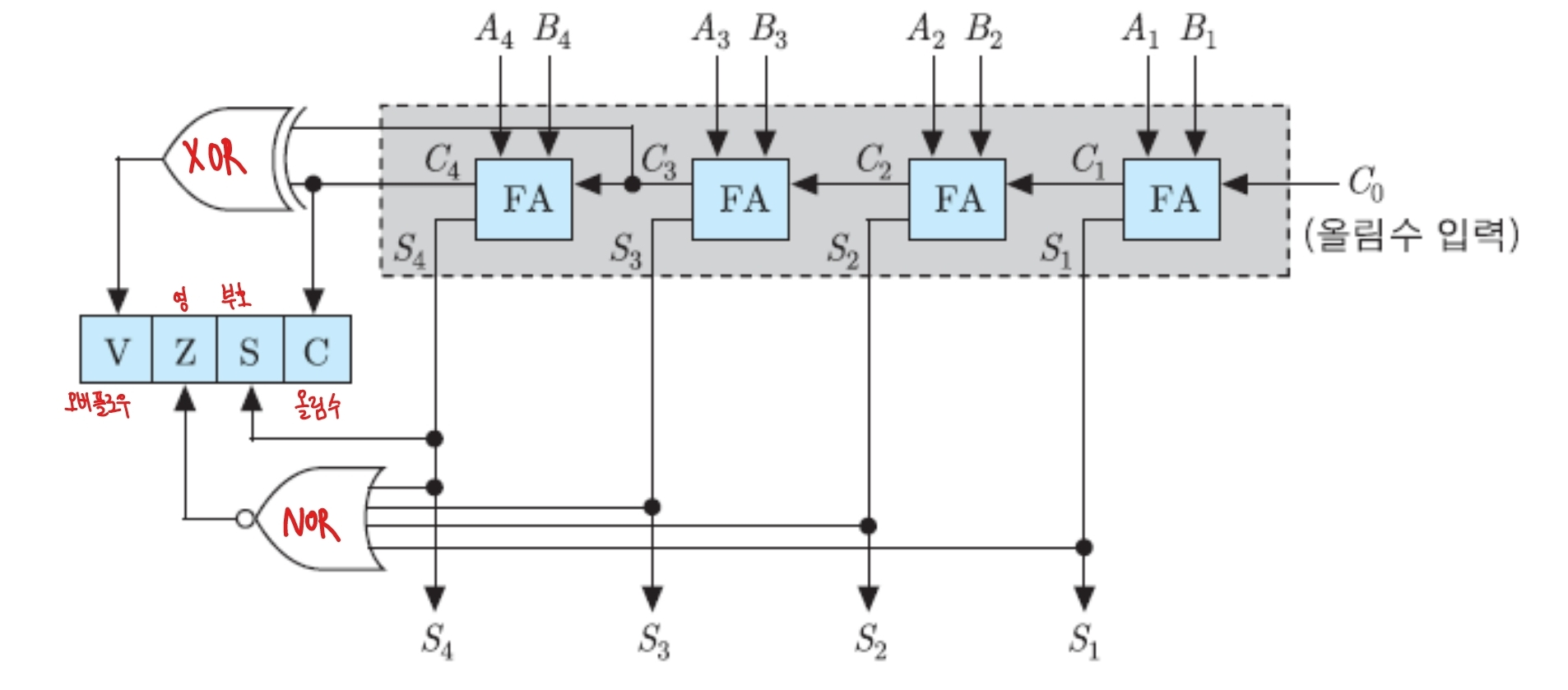
위 그림은 4비트 병렬 가산기와 상태 비트 제어회로를 나타낸 것이다.

병렬 가산기란 덧셈을 수행하는 하드웨어 모듈로 비트 수만큼 전가산기들을 연결하여 구성한다.
덧셈 연산 결과에 따라 C(올림수),V(오버플로우),Z(0),S(부호) 플래그들을 세팅한다.

오버플로우는 덧셈 결과가 그 범위를 초과하여 결과값이 틀리는 상태를 말한다.

(+6) + (+3) = +9

 0110
+0011
-----
 1001 = -7 (V=1)

뺄셈

뺄셈은 덧셈과 유사한 형식으로 진행되는데, 예를 들어 A - (+B) = A + (-B) 형식으로 덧셈을 이용하여 수행한다.

(+2) - (+6) = (+2) + (-6) = -4

 0010
+1010
-----
1100 = -4

덧셈과 뺄셈을 수행하는 하드웨어는 보수기를 거쳐 가산기에서 연산을하여 레지스터에 저장된다.

이러한 덧셈, 뺄셈 겸용 하드웨어 블록 구성도는 아래와 같다.

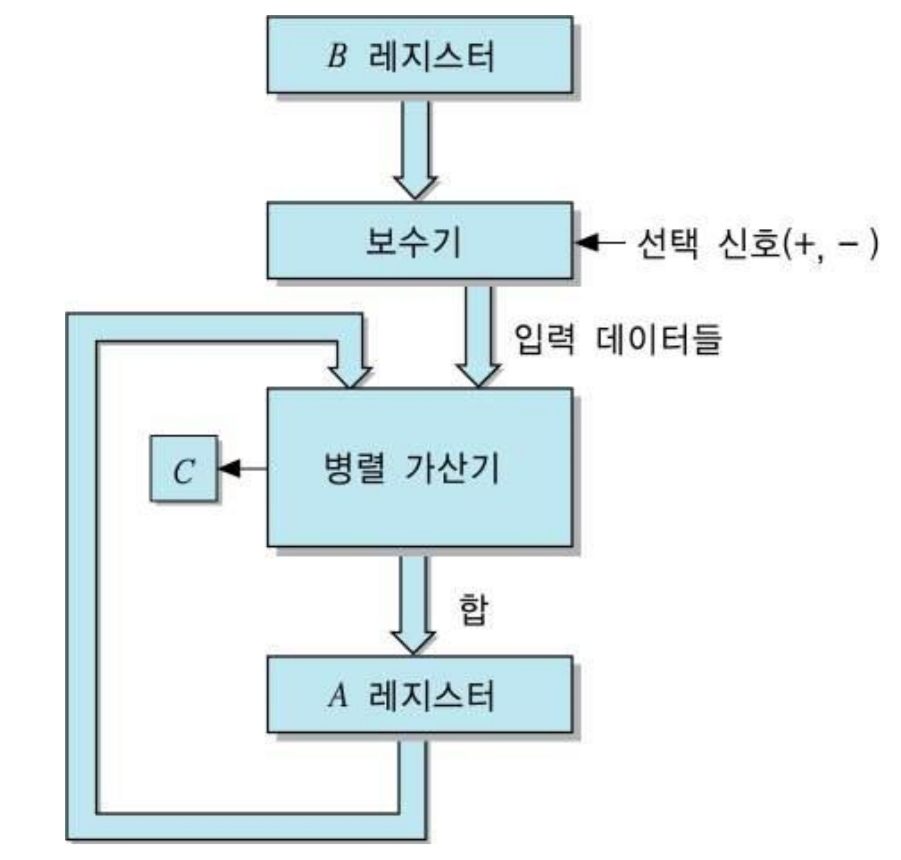
오버플로우는 덧셈과 마찬가지로 뺄셈 결과 범위가 초과하여 발생한다.

곱셈

부호없는 정수의 곱셈

부호 없는 정수의 곱셈은 각 비트에 대하여 부분 적계산을 수행한다.

    1101	-> 13 (피승수)
   x1011	-> 11 (승수)
   -----
    1101
   1101
  0000
 1101
 -------
10001111	-> 143

이러한 부호 없는 정수 승산기의 하드웨어 구성도는 아래와 같다.

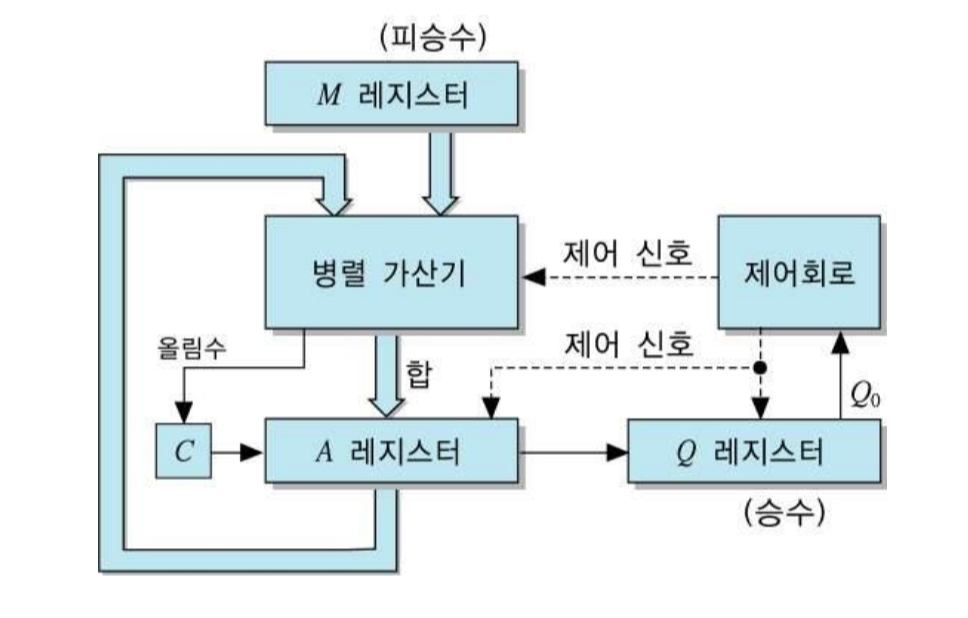
2의 보수곱셈

Booth 알고리즘 사용하고, 부호 없는 정수 승산기에 보수기 및 1-비트 레지스터를 추가한다.

아래는 Booth 알고리즘 흐름도이다.

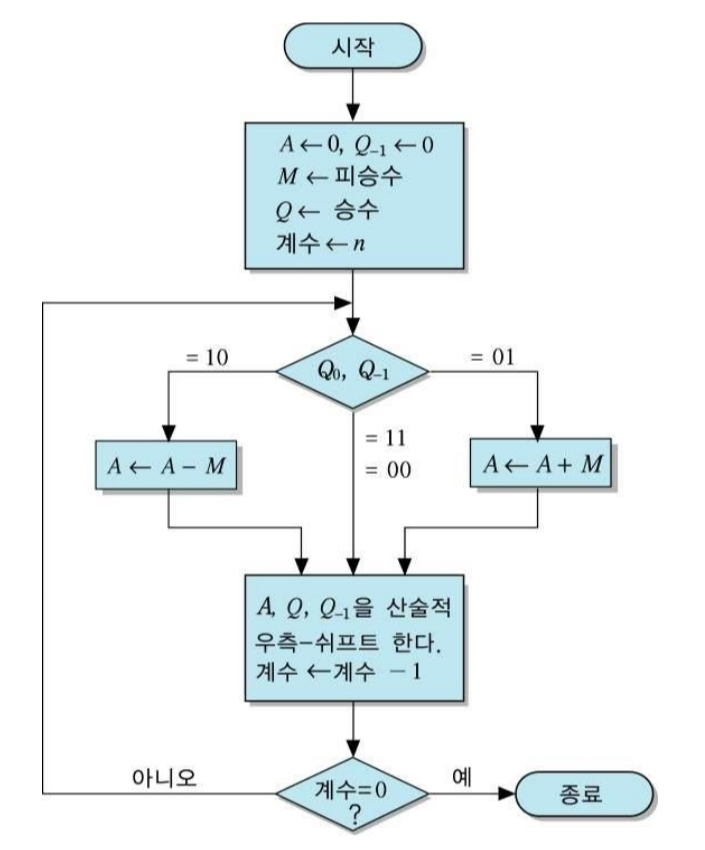
Booth 알고리즘을 적용하여 (-7) x (+3)을 계산하면 아래와 같다.

	  M = 1001 (-7)
   x  Q = 0011 (+3)
 	  --------
A Q  0111 0011		Q_0,Q_-1 = 10 이므로 피승수를 뺌
     
     0011 1001		우측 쉬프트 이후 계수는 4-1 = 3 
     
     0001 1100		Q_0,Q_-1 = 11 이므로 우측 쉬프트만 하고 계수는 3-1 = 2
     
     1010 1100		Q_0,Q_-1 = 01 이므로 피승수 더해줌
     
     1101 0110		우측 쉬프트 이후 계수는 2-1 = 1
     
     1110 1011	(-21)	Q_0,Q_-1 = 00 이므로 우측 쉬프트만 하고 계수는 0 -> 계산 종료

나눗셈

부호없는 2진 나눗셈

피제수를 제수로 나누어 몫과 나머지를 구한다.

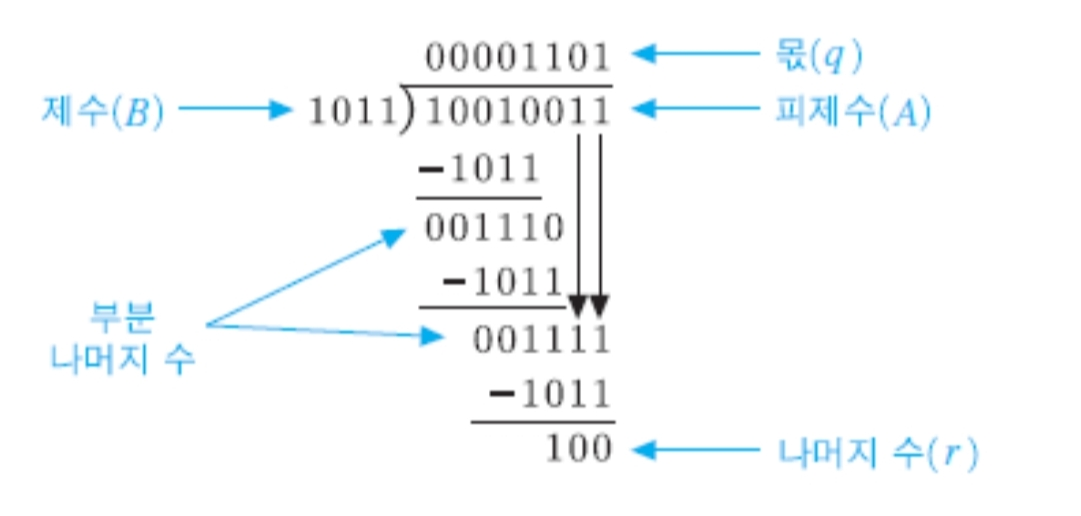
2의 보수 나눗셈

2의 보수 나눗셈은 2의 보수 곱셈과 다르게 좌측 쉬프트로 연산이 이루어진다.
2의 보수 나눗셈을 적용하여 (+7) ÷ (-3)을 계산하면 아래와 같다.

	  Q = 0111 (+7)
	÷ M = 1101 (-3)  
 	  --------
A Q  0000 0111		
     
     0000 1110		좌측 쉬프트
     1101			A와 M 부호 다르므로 A ← A+M
     0000 1110		A의 부호 다르므로 A의 원래값 복구
     0001 1100		좌측 쉬프트	
     1110			A와 M 부호 다르므로 A ← A+M
     0001 1100		A의 부호 다르므로 A의 원래값 복구
     
     0011 1000		좌측 쉬프트
     0000			A와 M 부호 다르므로 A ← A+M
     0000 1001		A = 0 이므로 Q_0 = 1로 세트
     
     0001 0010		좌측 쉬프트
     1110			A와 M 부호 다르므로 A ← A+M
     0001 0010		A의 부호 바뀌었으므로, Q_0 = 0 으로 세트하고 A의 원래값 복구
     
     				몫은 Q의 2의 보수인 1110
                    나머지는 A 레지스터인 0001

부동소수점 수의 표현

소수점의 위치를 이동시킬 수 있는 표현 방법이다.
일반적으로 N = (-1)^S M x B^E 형태이다

<S = 부호> <M = 가수> <B = 기수> <E = 지수>

  • 2진 부동소수점 수 (B = 2)

    • 단일정밀도 부동소수점 수 : 32비트

      지수가 늘어나면 표현 가능한 수의 범위가 확장되고, 가수가 늘어나면 정밀도가 증가한다.

    • 복수정밀도 부동소수점 수 : 64비트

  • 같은 수에 대한 부동소수점 표현

    • 같은 수에 대해 부동소수점을 여러가지로 표현할 수 있기에 정규화된 표현은 소수점 첫쨋자리를 가지고 있는 0.1xxx x 2^E 이다.

  • 바이어스 지수
    가수 비트를 0으로 하고, 지수 비트를 M x 2^(-127)으로 나타내어 부동소수점의 0 표현 방식에 대한 문제를 해결해준다.

예를 들어 바이어스 값 = 128, N = -13.625 일때 부동소수점 표현은 아래와 같다.

S = 1 (-)
E = 00000100 + 10000000(바이어스 128) = 10000100
M = 10110100000000000000000

부동소수점 수의 표현 범위

32비트 데이터 형식의 표현 가능한 수의 범위


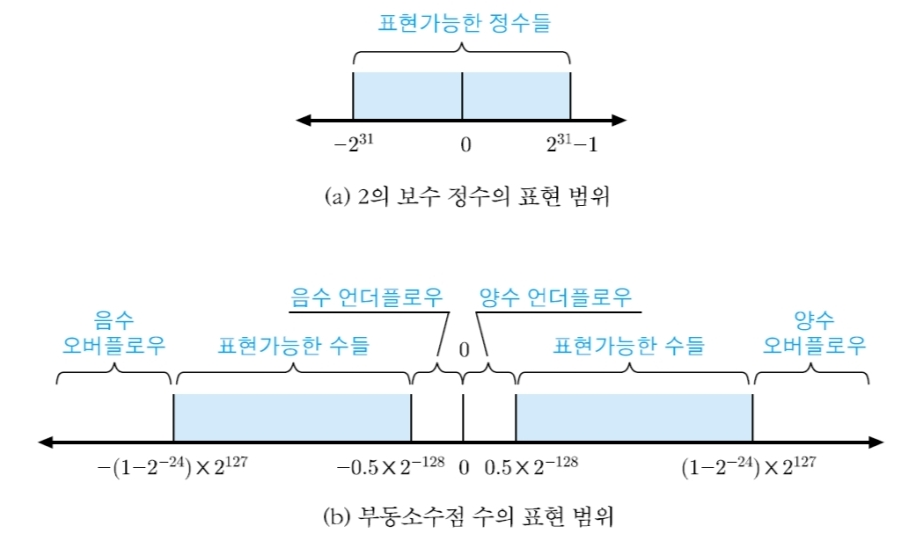
부동 소수점은 0 근처에 수들이 더 밀집되어 있다.

profile
심영민
코딩너무어려운대 어떡할과 재학중
이전 포스트

제어 유니트

다음 포스트

기억장치

0개의 댓글

관련 채용 정보