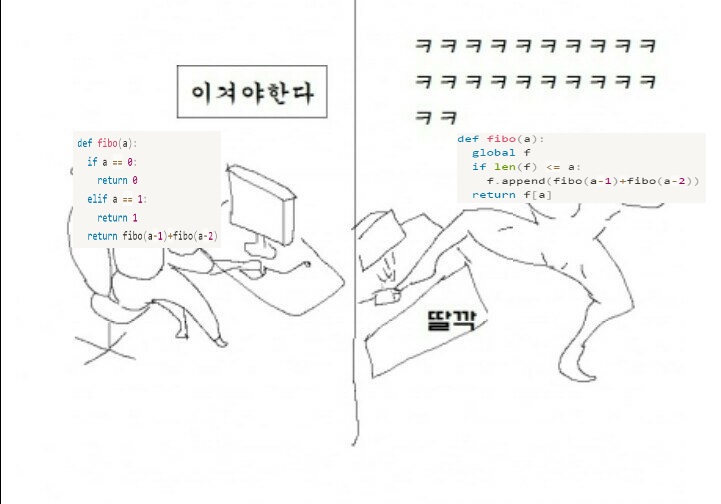
이하 동적계획법 알고리즘을 DP라고 부를겁니다.
DP란 무엇일까?
대부분 이야기하는 DP는 큰 문제에 대해 작은 문제들로 쪼개서 먼저 해결하며 그 결과들을 이용해 큰 문제를 비교적 간단하게 해결하는 기법이다.
이 기법을 그림으로 보자면 다음과 같다.
점점 야금야금 작은 문제들을 해결하며 큰 문제를 해결한다.
Tabulation, Memoization
DP의 전형적인 형태 Tabulation 상향식(bottom-up) 접근 방식이라 한다.
그리고 반대 버전같지만 크게 보면 비슷한 방식이 하나 있는데, 이를 Memoization 하향식(top-down) 접근 방식이라 한다.
그렇다면 두 방식의 차이는 무엇일까?
Tabulation(bottom-up)
도표라는 뜻을 가지고 있는데, 이 방식은 재귀호출을 사용하지 않기 때문에 시간과 메모리를 줄일 수 있다.
Tabulation을 간단한 코드로 보자면 다음과 같다.
n = int(input())
arr = list(map(int, input().split()))
dp = [0 for i in range(n)]
dp[0] = arr[0]
for i in range(1, n):
dp[i] = max(dp[i-1]+arr[i], arr[i])
print(max(dp))해당 코드에서는 dp 배열을 통해 초기 값을 저장하고, 그 뒤로 점화식을 통해 하나씩 나아간다.
이 코드는 보면 알겠지만, 시간복잡도는 O(n)만큼 걸림을 알 수 있다.
위의 코드는 가장 큰 값을 가진 수열의 합을 찾는 코드인데, 이를 DP가 아닌 하나하나 찾아보는 방식으로 코드를 짰다면 다음과 같을 것이다.
n = int(input())
arr = list(map(int, input().split()))
answer = []
for i in range(n):
for j in range(i, n):
answer.append(sum(arr[i:j+1]))
print(max(answer))이렇게 작성하면 O(n^3)만큼의 시간복잡도가 발생한다.
Memoization(top-down)
이전에 계산한 값을 메모리에 저장하여 중복적인 계산을 제거하여 전체적인 실행속도를 빠르게 한다.
이를 다르게 정의하면 큰 문제를 해결하기 위해 작은 문제를 호출한다고 보면 된다.
그래서 이를 구현하는 예시로 피보나치 수열이 있다.
n = int(input())
global f
f = [0, 1]
def fibo(a):
global f
if len(f) <= a:
f.append(fibo(a-1)+fibo(a-2))
return f[a]
print(fibo(n))위와 같은 코드는 이미 몇 번째 피보나치 수열의 값을 기억하기 때문에 O(n)의 시간복잡도가 발생한다.
하지만 Memoization을 사용하지 않는다면 코드는 다음과 같고, 이는 O(2^n)의 시간복잡도가 발생한다.
n = int(input())
def fibo(a):
if a == 0:
return 0
elif a == 1:
return 1
return fibo(a-1)+fibo(a-2)
print(fibo(n))React Memoization
React에서 컴포넌트가 렌더링하는 규칙에는 크게 세 가지가 존재한다.
state나props가 변경되었을 때forceUpdate()를 실행했을 때- 부모 컴포넌트가 렌더링 되었을 때
만약 앱의 규모가 커진다면 계속 렌더링하게 될 것이고, 이는 서비스 사용에 불편함을 느낄 것이다.
그래서 이를 해결하기 위해 useCallback, useMemo 등으로 memoization을 적용한다.
그렇다면 두가지 방식은 어떻게 작동하는지 살펴보겠다.
useCallback
useCallbackis a React Hook that lets you cache a function definition between re-renders.
이 리액트 훅은 재렌더링 후 정의한 함수를 캐싱해준다.
(여기서 캐싱은 복사본을 저장하여 빠르게 복사본을 쓰는 방식을 나타낸다.)
useCallback에는 매개변수로 함수와 종속성이 들어가야한다.
import { useCallback } from 'react';
function ProductPage({ productId, referrer, theme }) {
const handleSubmit = useCallback((orderDetails) => {
post('/product/' + productId + '/buy', {
referrer,
orderDetails,
});
}, [productId, referrer]);
// ...만약 이 코드에서 종속성으로 들어간 배열들 중에 하나라도 변경된다면 해당 함수를 사용하는 JSX는 다시 렌더링 된다.(그 전에는 렌더링되지 않는다.)
그러니까 종속성이 변화하기 전까지는 그냥 기존 JSX복사본을 가져온다는 의미이다.
위에서 봤던 Memoization처럼 컴포넌트 구조도 잘 보면 Memoization과 비슷함을 볼 수 있다.
useMemo
useMemois a React Hook that lets you cache the result of a calculation between re-renders.
useMemo는 리렌더링 사이에 계산된 결과 값을 캐시해주는 훅이다.
const visibleTodos = useMemo(
() => filterTodos(todos, tab),
[todos, tab]
);
return (
<div className={theme}>
<p><b>Note: <code>List</code> is artificially slowed down!</b></p>
<List items={visibleTodos} />
</div>
);두 번째 인자의 값이 변경하면 리렌더링하며 해당 결과값을 바꾼다.
얼핏 보면 useCallback과 비슷해 보이지만, 약간 다르다.
- 먼저
useMemo는 값을 반환하고useCallback은 함수를 반환한다. useEffect에서 종속성이 자주 바뀌어서 빈번하게 발생하는 사이드이펙트를useCallback으로 감싸서 특정 상황에서만 작동하게끔 해결할 수 있다.
결론
사실 DP에 관해서 여러 문제들을 소개할까 싶었지만, 리액트에서 Memoization과 같은 기능을 하는 훅들이 있어서 그것에 더 흥미가 있었다.
위에서 살짝 언급했지만, 리액트는 index.js에서 보통 컴포넌트가 렌더링하여 트리모양의 컴포넌트 구조에서 점점 자식 컴포넌트로 렌더링 하는 모습을 볼 수 있다.
그리고 이 과정을 Memoization으로 렌더링을 줄이게 된다면, 확실히 애플리케이션의 속도를 줄일 수 있음을 확신했다.