코드트리 블로그 챌린지 글을 계속 이어나가기 위해 제목과 시리즈 이름을 바꿔서 진행합니다.
(위의 진단은 다음에...)
이번엔 arr.sort()만으로 하는 정렬이 아닌 실제로 많이 하는 정렬에 대해 알아보자.
시간이 많이 걸리지만 간단한 정렬
버블 정렬
이름 대로 거품이 껴 있는 정렬방식이다.
왜 거품이 껴있냐면 어떤 상황이든 O(n^2)의 수행시간이 걸리기 때문이다.
코드를 보자면
# 기존 버블 정렬
arr = [...]
n = len(arr)
for i in range(n):
for j in range(n-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
print(*arr)
# 개선된 버블 정렬
arr = [...]
n = len(arr)
sort = False
while sort != True:
sort = True
for i in range(n-1):
if arr[i+1] < arr[i]:
sort = False
arr[i+1], arr[i] = arr[i], arr[i+1]
print(*arr)
이렇게 정렬될 때 까지 배열의 해당 위치와 해당 위치의 바로 옆을 비교해서 오름차순이 아니면 스왑하는 방식이다.
선택 정렬
선택 정렬은 해당 위치에서 오름차순 기준 가장 작은 값을 찾아 해당 위치에 스왑하는 정렬이다.
말 그대로 계속 순회하며 매번 선택해야 하므로 어떤 순간에도 O(n^2)이 걸리게 된다.
arr = [...]
n = len(arr)
for i in range(n-1):
mininum = i
for j in range(i+1, n):
if arr[mininum] > arr[j]:
mininum = j
arr[mininum], arr[i] = arr[i], arr[mininum]
삽입 정렬
삽입 정렬은 현재 위치에서 앞에 있는 배열들은 정렬 되어 있다 가정하고 현재 위치에 있는 요소를 앞으로 이동하여 적절한 크기에 위치하도록 삽입한다.
예를 들어, 현재 for문에서 5번째 인덱스에 접근할 때, 이미 0번째 인덱스 부터 4번째 인덱스까지는 정렬되어 있어서, 5번째 인덱스의 값을 오름차순에 맞게 삽입하면 된다.
코드를 보면 이해가 될 것이다.
arr = [...]
n = len(arr)
for i in range(1, n):
j = i-1
now = arr[i]
while j >= 0 && arr[j] > now:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = now
print(*arr)이미 배열이 정렬되어 있다면 O(n)밖에 걸리지 않고, 배열이 내림차순이라면 O(n^2)이 걸린다.
기수 정렬
기수 정렬은 기존의 정렬들과 다르게, 배열의 요소의 맨뒤 자릿수부터 1자리씩 해당하는 숫자를 다른 배열에 넣으면서 기존 배열에는 해당 자릿수 순으로 마지막 자릿수까지 정렬한다.
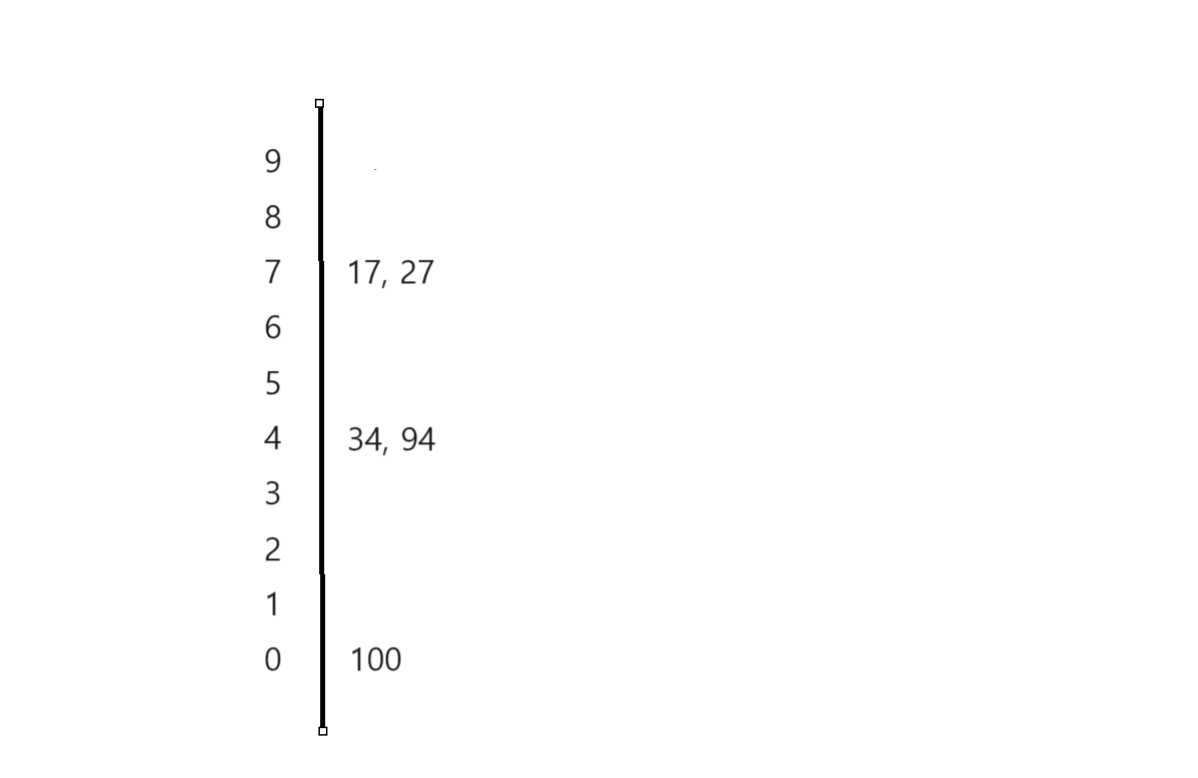
말이 어렵지만 만약 17, 100, 34, 27, 94라는 배열이 있다면, 1번째 자릿수에서 이렇게 분류한다.
이렇게 해서 마지막 자릿수까지 분류하면 정렬이 된다.
앞으로 나오는 정렬들은 해당 문제와 같은 형식으로 코드가 입출력이 작성되어 있을 것이다.
n = int(input())
arr = list(map(int, input().split()))
m = len(str(max(arr)))
for i in range(m):
now = 10**i
a = [[]for k in range(10)]
for j in range(n):
temp = (arr[j] // now) % 10
a[temp].append(arr[j])
ta = []
for j in range(10):
for k in range(len(a[j])):
ta.append(a[j][k])
if len(arr) == n and len(ta) == n:
arr = ta[:]
else:
arr += ta
print(*arr)
기수 정렬의 수행시간은 m = 가장 긴 자릿수의 길이면, O(n*m)이 된다.
복잡하지만 시간은 많이 안걸리는 정렬
여기서 부터 많이 복잡해진다.
병합 정렬
병합 정렬은 계속 절반으로 쪼개서 가장 작은 단위부터 정렬하며 합치는 정렬이다.
계속 절반으로 쪼개는 과정에서 logn번 걸리고, 배열들을 합치는데 n번 걸리므로 총 수행시간은 O(n*logn)이 걸리게 된다.
n = int(input())
arr = list(map(int, input().split()))
def merge(arr, low, high):
if low < high:
mid = (low+high)//2
merge(arr, low, mid)
merge(arr, mid+1, high)
merge_sort(arr, low, mid, high)
def merge_sort(arr, low, mid, high):
i, j = low, mid+1
ta = []
while i <= mid and j <= high:
if arr[i] < arr[j]:
ta.append(arr[i])
i += 1
else:
ta.append(arr[j])
j += 1
while i <= mid:
ta.append(arr[i])
i += 1
while j <= high:
ta.append(arr[j])
j += 1
for i in range(low, high+1):
arr[i] = ta[i-low]
return arr
merge(arr, 0, n-1)
print(*arr)
퀵 정렬
퀵 정렬은 0번째 인덱스의 값을 기준으로 해당 값보다 작은 값과 큰 값을 나눠서 정렬해가는 방법이다.
평균적으로 O(n*logn)이 나오지만,
최악의 경우(0번째 인덱스가 가장 크거나 작은 경우) O(n^2)이 걸릴 수 있다.
n = int(input())
arr = list(map(int, input().split()))
def quick(arr, low, high):
pivot = arr[high]
i = low-1
for j in range(low, high):
if arr[j] < pivot:
i += 1
arr[j], arr[i] = arr[i], arr[j]
arr[i+1], arr[high] = arr[high], arr[i+1]
return i+1
def quick_sort(arr, low, high):
if low < high:
mid = quick(arr, low, high)
quick_sort(arr, low, mid-1)
quick_sort(arr, mid+1, high)
quick_sort(arr, 0, n-1)
print(*arr)
힙 정렬
힙 정렬은 파이썬에서 heapq를 사용하면 되지만, 이진 트리를 배열로 쉽게 구현 가능해서 코드 작성이 된다.
가장 작은 값을 배열에서 빼는 과정이 logn번 걸리고 이런 과정을 n번 반복하므로 O(n*logn)이 걸린다.
import heapq
n = int(input())
arr = list(map(int, input().split()))
heapq.heapify(arr)
while arr:
print(heapq.heappop(arr), end=' ')stable/in-place
stable
배열 내부에 같은 값이 있다면, 같은 값들의 인덱스 순서가 바뀌지 않는 정렬을 stable한다고 한다.
대표적으로 퀵 정렬이 stable하지 않은 정렬이다.
in-place
배열을 하나 더 사용하지 않고 정렬 가능하면 in-place한 정렬이다.
대표적으로 기수 정렬은 in-place하지 않은 정렬이다.