코드트리 블로그 챌린지 글을 계속 이어나가기 위해 제목과 시리즈 이름을 바꿔서 진행합니다.
 어?
어?
처음부터 이럴 생각은 아니었지만, 새벽에 하다보니 이런 결과가 나오게 되었다.
나중에 하는 걸로 하고
일단 개인적으로 cs를 공부하고 싶다는 생각이 들어서 novice high의 문제집을 이용해 자료구조 & 알고리즘복습을 해볼 것이다.
수도코드
우리가 이해하기 쉽게 작성한 코드
말 그대로 우리가 이해하기 쉽게끔 기존 언어의 문법을 따르지 않고 작성했다.
예를 들어,
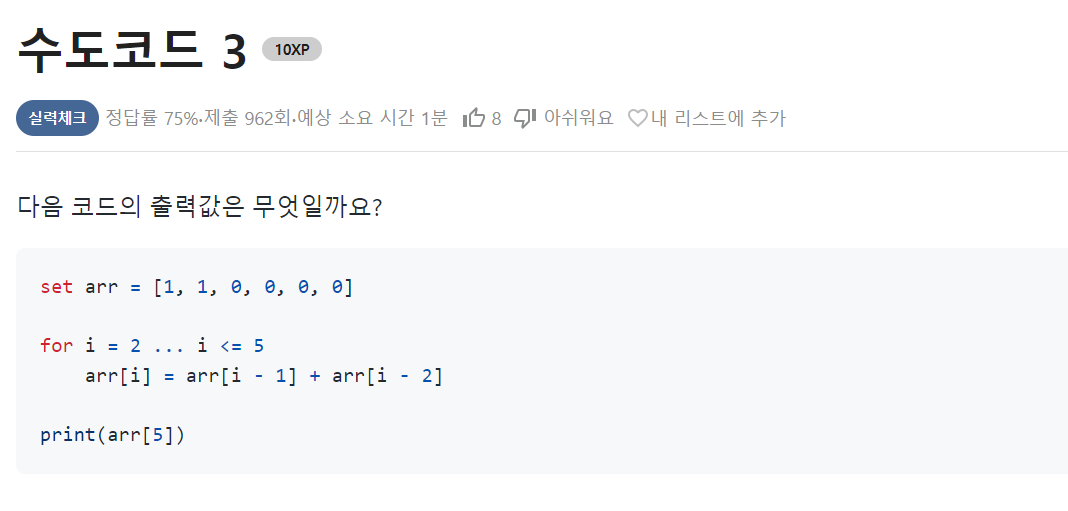
문제 링크: https://www.codetree.ai/missions/6/problems/pseudo-code-3?&utm_source=clipboard&utm_medium=text
이런 코드를 보면 기존 언어들의 문법을 모르지만 단어의 뜻을 통해 유추해 볼 수 있다.
왜 수도코드를 사용하는가?
그 이유는 코딩 입력 전, 수도코드를 통해 명확한 사고 정립을 하여 설계하는 것에 도움을 주기 때문이다.
점근적 표기법
여기서 점근적이란 말은 가장 큰 영향을 주는 항만 계산한다는 의미이다.
우리가 코드를 작성하다고 제출했을 때 테스트케이스에서 시간초과와 같은 문구를 본 적있을 텐데, 이는 언어의 특성 혹은 컴파일러 속도 등에 따라 나올 수 있지만 대부분의 문제는 알고리즘의 성장률에 문제가 있다.
(참고로 언어의 특성과 같은 이유로 시간초과가 나올려면 엄청난 고인물이 되어야 볼 수 있다.)
성장률에서 불필요한 부분인 상수와 계수를 없애고, 데이터가 많을 수록 가장 큰 처리를 하는 차수를 찾아 표기하는 점근적 표기법을 사용하게 되는데, 이 때 점근적 표기법을 사용하는 방식은 크게 3가지가 있다.
여기서 만약 식이 3*n^3 + 2*n^2 + 5라면, 각각 앞에 붙어 있는 3, 2와 5를 다 1로 바꿔서 생각해야한다.
(데이터의 양이 무한대로 나아가면 차수 앞에 붙어 있는 계수는 의미가 없어진다.)
빅오 표기법
현재 가장 높은 차수 보다 같거나 높은 식 + 시간복잡도와 공간복잡도를 계산하는 데 사용하는 표기법
정의
-> O(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤f(n)≤cg(n) for all n≥n0}
예시
n^2 + n + 1 -> O(n^2)
6*n^3 + n^2 + 1 -> O(n^3)
참고로, 가장 높은 차수가 n^2일 때 O(n^100)도 맞는 말이다.
(하지만 이런식의 접근은 개인적으로 별로 권장하진 않는다.)
최대한 가장 높은 차수와 같거나 비슷한 식을 빅오 표기법으로 사용하는 것이 성장률을 분석하는데 도움이 된다.
오메가 표기법
현재 가장 높은 차수 보다 같거나 낮은 식
정의
-> Ω(g(n)) = {f(n) : there exist positive constants c and n0 such that 0≤cg(n)≤f(n) for all n≥n0}
예시
n^2 + n + 1 -> Ω(n^2)
6*n^3 + n^2 + 1 -> Ω(n^3)
빅오 표기법과 반대로 오메가 표기법에서는 가장 높은 차수가 n^3일 때, Ω(n)도 맞는 말이다.
(하지만 이런식의 접근은 개인적으로 별로 권장하진 않는다.)
세타 표기법
현재 가장 높은 차수와 같은 식 (빅오 표기법과 오메가 표기법의 교집합인 식)
예시
n^2 + n + 1 -> Θ(n^2)
6*n^3 + n^2 + 1 -> Θ(n^3)
이 표기법은 정확히 가장 높은 차수와 일치해야한다.