[알고리즘] 시간 복잡도, 공간복잡도

Heewon Seo·2023년 9월 15일

공간복잡도 시간복잡도 코드트리 코딩테스트 코딩테스트실력진단

[알고리즘]

목록 보기

2/5

코드트리 블로그 챌린지 글을 계속 이어나가기 위해 제목과 시리즈 이름을 바꿔서 진행합니다.

약간의 발전

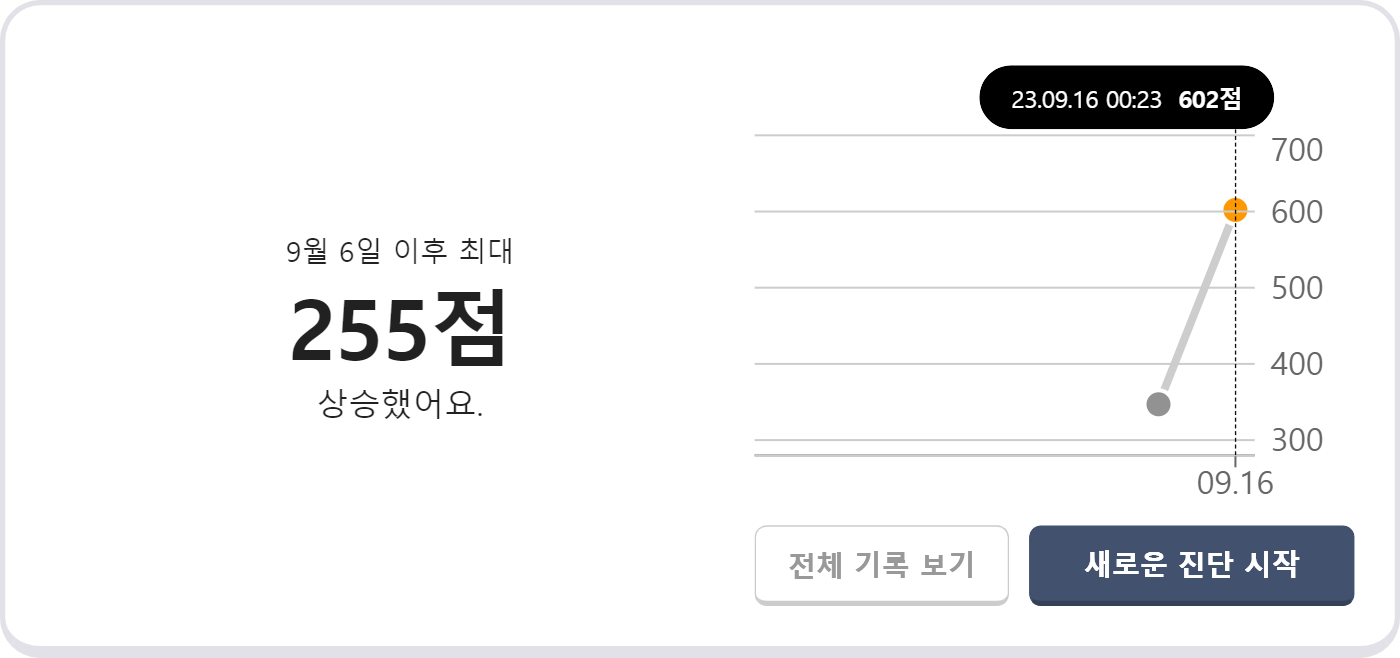
어제 봤던 문제와 같은 문제들이 많아서 1문제 빼고 다풀었다!
하나는 정수형 숫자들 나열하는 문젠데 한번 찾아봐야겠다.

시간 복잡도

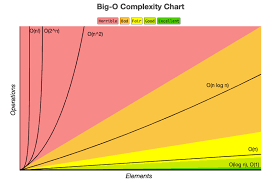
코드를 짤 때에는 효율성을 많이 따지게 된다. 그래서 우리는 일단 시간 복잡도에 대해 알아 볼 것이다.

우리가 맨 처음 풀었던 문제들을 보면 대부분 루프를 사용하지 않은 단순 연산하는 문제들을 마주친다.
예를 들어,

a = a+1
print(a)

라는 코드를 본다면, a변수에는 한번의 단순한 연산(덧셈)을 실행하므로 O(1)의 시간복잡도라고 가정하며, 마찬가지로, print와 같은 메서드도 단순히 출력하므로 O(1)의 시간복잡도라고 가정한다.

시간 복잡도를 알면 어떻게 효율성을 따질까?

보통 대부분의 코딩 테스트 환경은 1초에 1억번 for문을 통해 단순 연산을 해야 1초가 나온다.
그리고 코딩 테스트 문제들은 대부분 1초 ~ 10초 정도 시간 제한이 걸려 있다.

그래서 우리는 코딩 테스트 문제에 적혀 있는 자료의 양을 보고 어느 정도 수행시간 이하를 요구하는 지 파악해야 한다.(그래야 시간초과가 나오지 않는다.)

예를 들어, 자료의 양이 10만개 정도라면, O(nlogn)이하의 시간 복잡도를 요구한다. 그래야 연산하는데 1억번보다 적게 나오기 때문이다.

O는 왜 쓸까?

오메가 표기법은 실제 코드보다 빠르다고 파악해 버릴 수 있기 때문에 효율성을 파악하는데 위험하고, 세타 표기법은 실제 코드가 정확히 해당 시간 복잡도를 나타내기 어렵기 때문에 빅오 표기법이 최악의 경우를 판단해 가장 안전하게 시간 복잡도를 나타낼 수 있기 때문이라고 한다.

이 코드의 시간 복잡도는 어떻게 될까?

링크: https://www.codetree.ai/missions/6/problems/time-complexity-3?&utm_source=clipboard&utm_medium=text

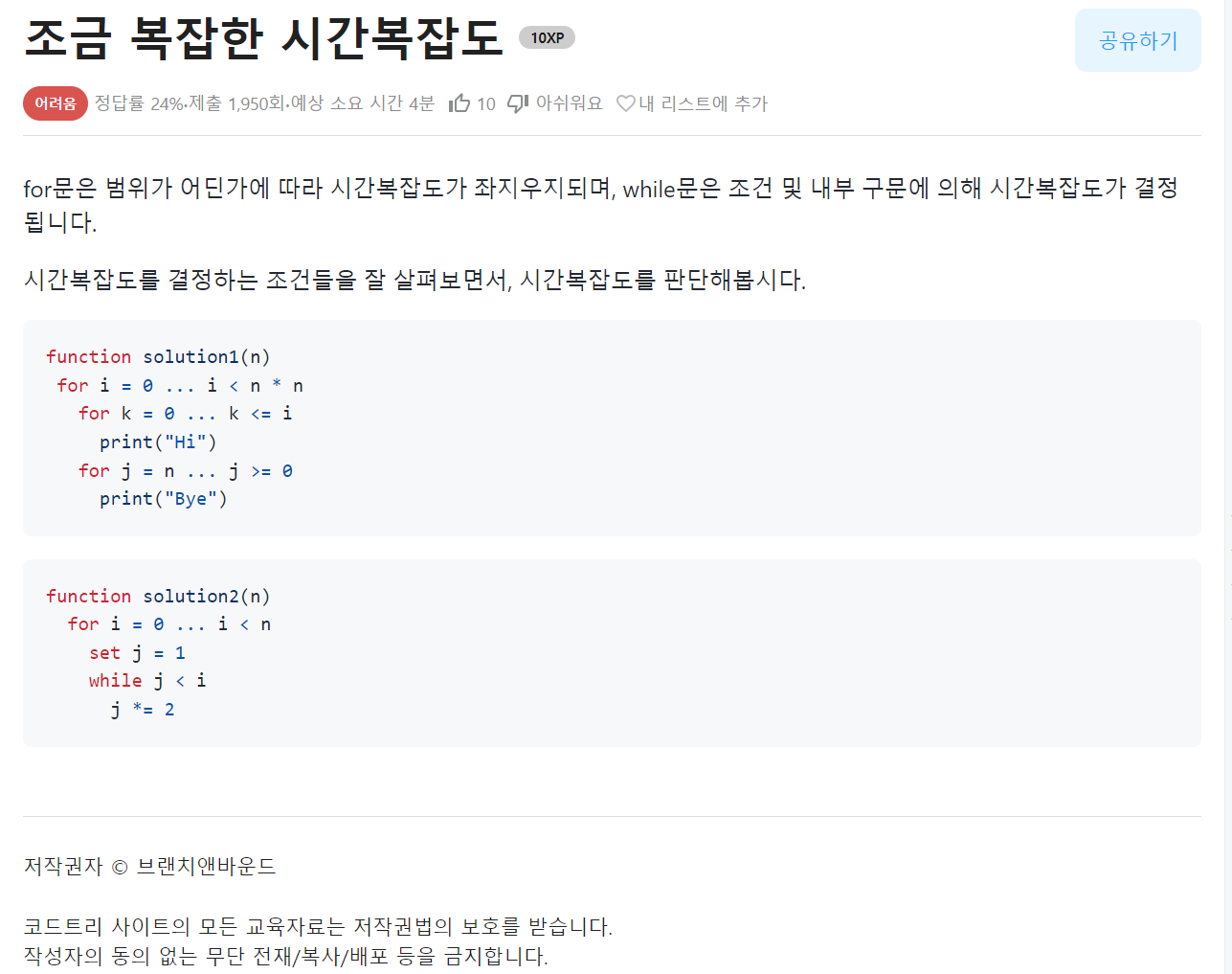
위의 코드를 먼저 보면,

i가 n^2번 돌아가는 동안
k는 i번 돌아간다.
j는 n번 돌아간다.

이런 상태인데, 여기서 i번 돌아가는 것은 해당 이중 for문이 1, 2, 3 ... n^2번 돌아간다는 이야기다.
그래서 1부터 n^2까지 모두 더하면 (1+n^2)*(n^2)/2가 나오는데, 이는 가장 큰 차수인 n^4로 O(n^4)라 할 수 있다.

아래의 코드는