데이터 과학 기초

Randomness

Comparison and Booleans

비교 연산의 결과는 bool 값으로 나타난다.

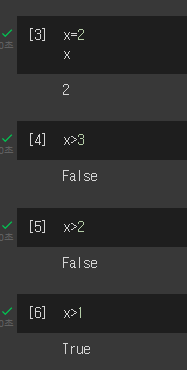
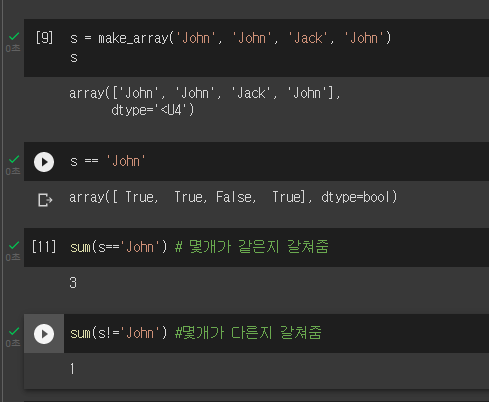
bool type의 list or array의 sum 연산은 True 값만 세서 반환한다.

• False는 0값을 나타내고 True는 1을 나타내기때문이라고 생각하면 된다.

Applying a Function to a Row

Rows

테이블의 Row는 item을 가지고 있다.

r = t.row(0)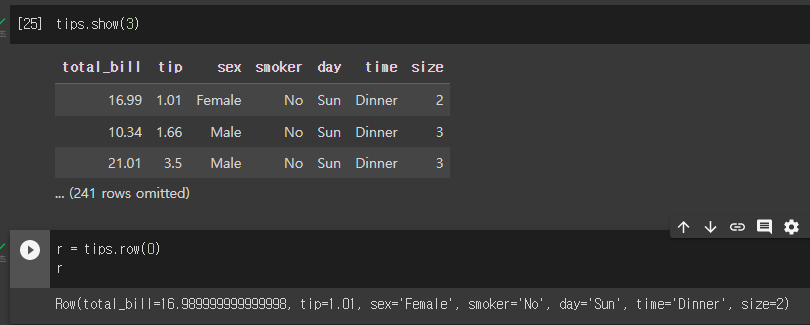

• r은 index 0의 row이다.

• 반환 타입은 table의 row로 나온다!! array가 아니다!

• 

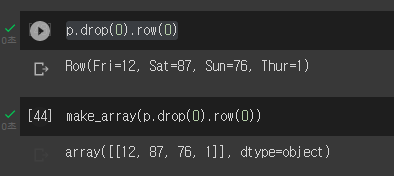
  • array로 만들고 싶다면 반환값을 make_array(반환값)or np.array()을 통해 형변환을 하면 된다!!

r.item(0)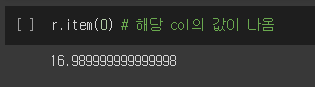

• r행의 0번째 col 값이 나온다.

sum(r)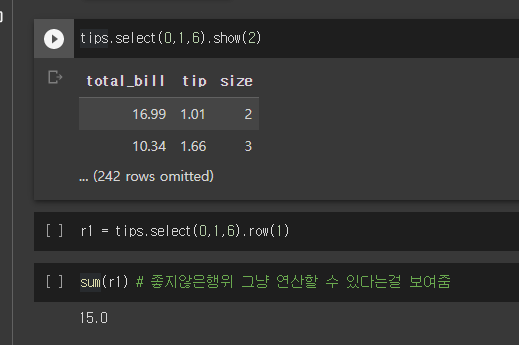

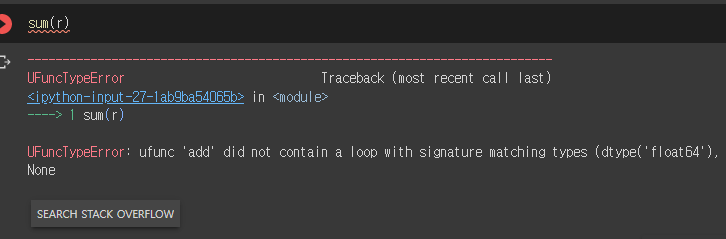
• 행의 값을 다 더할수도 있다.
• 근데 r의 데이터 타입이 다 같아야지 계산이 가능하다.
  • 아니면 오류뜸

Table의 row의 값을 다 더하고 싶을때??

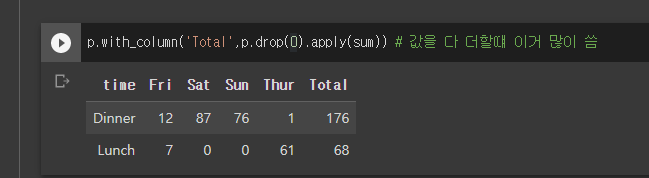
• table.apply(sum)을 적용하자
  • 이때 근데 타입이 다 넘버여야만함!!

Control Statements

프로그램에서 수행되는 계산의 순서를 제어한다.

if문 뭐 그런거,,,for문...

Random Selection

np.random.choice(배열or리스트,뽑을 횟수)

• 랜덤하게 고른다.
• 뽑을 횟수만큼 랜덤하게 값을 고름
  • 뽑을 횟수가 2이상이라면 배열로 리턴함

Appending Arrays

np.append(배열,값)
np.append(배열1,배열2)

• 값이 배열에 추가된 배열을 반환한다.
• 값은 배열과 같은 타입을 가져야한다.
  • array는 같은 타입만 허용한다.
• 배열1에 배열2가 추가된 배열을 반환한다.
• 배열 2는 배열 1과 타입이 같아야한다.

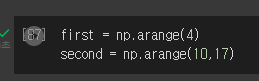
• first는 0~3까지 배열
• seconde는 10~16까지 배열

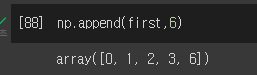
• first에 숫자 6을 붙이면 그냥 6이 배열에 붙음

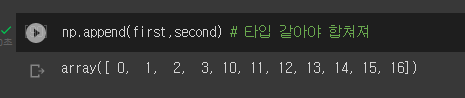
• 두 값 모두 배열을 넣으면 배열1에 배열2가 붙어

Iteration

• for문은 반복문이다.
  • 다들 잘 알 것이다.

for i in array:
  print(i)

• array 길이 만큼 반복해 for문 안에 동작을 실행한다.

Finding Chances

기본 상식

0: 가장 낮은 값

• event의 발생 가능성이 없다.
  • 일어날 확률이 없다

1: 가장 높은 값(100%)

• event가 발생할 확률이 확실하다
  • 무조건 일어난다

만약 어떠한 event의 가능성이 70%라면 그 event가 일어나지 않을 확률은

• 100% - 70% = 30%
• 1-0.7 = 0.3

똑같이 일어날 수 있는 결과

모든 결과가 동등하게 발생한다고 가정했을 때, 사건 A의 확률은...

• A가 일어날 확률 = A가 일어나는 결과의 수 / 전체 결과의 수

곱셈 규칙

A와 B 사건이 모두 일어날 가능성은

A,B사건이 모두 일어날 확률 = A확률 * A가 일어나고 B가 일어날 확률

• 두 확률 각각 일어나는 확률보다 작거나 같다.
• 만족해야할 조건이 많을 수록 그것이 일어날 확률은 작아진다.

Ex (곱셈규칙)

3장의 카드가 있다(1,2,3)
3장을 섞어서 2장을 랜덤으로 뽑는다
1번 다음 2번 카드를 뽑을 확률은??

• 1/3 * 1/2 = 1/6

덧셈 규칙

A라는 사건이 두가지 방법으로 발생할 수 있다면 가능성은

A확률 = A확률1 + A확률2

• 정답이 각 개별 방법의 확률보다 크거나 같다.

EX (덧셈 규칙)

3장의 카드가 있다(1,2,3)
3장을 섞고 2장을 한번에 뽑는다
1번과 2번을 뽑을 확률은?

• 3장중 2장을 뽑으면 된다
  • 그러므로 2/3이다.
  • 1과2를 뽑는경우(1/3)+2와1을 뽑는경우(1/3) = 2/3

문제풀이 방법

1. 첫 번째 재판이 무엇인지 자문해 보세요. 확률을 알고 있는 명확한 대답(예: "6"이 아님)이 있으면 거의 확실하게 곱셈 규칙을 사용하여 프로세스를 계속할 수 있습니다.

2. 명확한 답이 없는 경우(예: "K일 수도 있고, Q일 수도 있지만, 다음 답은 Q일 수도 있고, K일 수도 있습니다."), 이벤트가 발생할 수 있는 모든 뚜렷한 방법을 나열하고 기회를 더합니다.

3. 만약 위의 목록이 길고 복잡하다면, 보어를 보세요. 보수가 더 간단하면(예: "최소 하나"의 보수가 "없음") 그 확률을 찾아 1에서 뺄 수 있다.

• 어떠한 확률을 구한다
• 그 값이 특수한 상황에 일어나는 확률에 대해 시뮬레이션을 한다.
• 상황마다 일어나는 확률에 대해 맵핑한다.