Raytracing

• 카메라로부터 쏜 ray가 물체에 부딪혀 돌아오게 되는 경로를 추적하여 색을 입히는 그래픽 기법이다.

Cam

viewport

void	set_cam(t_scene *scene, t_cam *cam)
{
	double	vp[2];
	t_vec3	w;
	t_vec3	u;
	t_vec3	v;

	vp[1] = 2 * tan(cam->fov / 2 * M_PI / 180);
	vp[0] = vp[1] * (double)scene->xres / scene->yres;
	w = normalize(vscale(cam->nv, -1));
	set_uv_axis(w, &u, &v);
	cam->hor = vscale(u, vp[0]);
	cam->ver = vscale(v, vp[1]);
	cam->llc = vsub(cam->o, vscale(cam->hor, 0.5));
	cam->llc = vsub(cam->llc, vscale(cam->ver, 0.5));
	cam->llc = vsub(cam->llc, w);
}

• miniRT에서는 camera의 위치와 카메라가 보는 방향을 나타낼 normal vector, 화각 fov를 받는다.

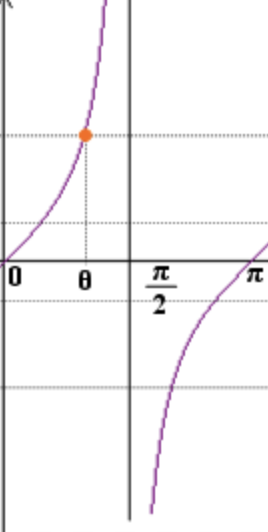
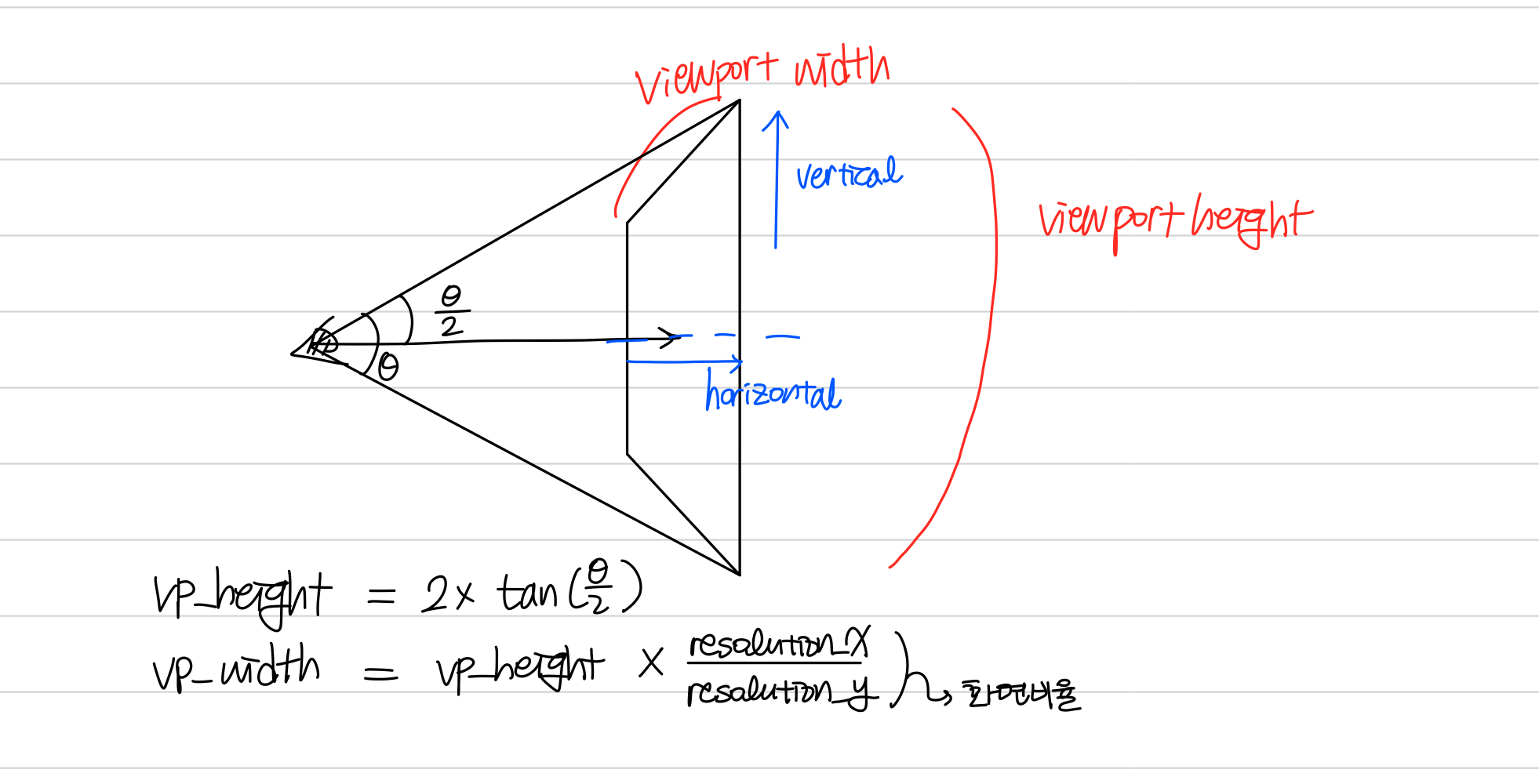
• fov를 이용해 먼저 viewport를 설정해주게 되는데, viewport의 height는 입력받은 fov값 / 2 의 tangent값을 2 곱해준 길이가 된다.
  (tangent 그래프가 π/2 를 기준으로 음수 값이 되니까 2로 나눈 값을 다시 2 곱해주는 식으로 사용하는 것 같다. 파싱할 때 0~180 사이 값만 받을 수 있다.)
  

• C언어의 tan 함수는 라디안 값을 인자로 사용하기 때문에 π/180 을 곱해주었다.
  

• viewport의 width는 height에 화면 비율만큼 곱해 구해준다.

axis

• https://raytracing.github.io/books/RayTracingInOneWeekend.html#rays,asimplecamera,andbackground/sendingraysintothescene

w = normalize(vscale(cam->nv, -1));
set_uv_axis(w, &u, &v);

void	set_uv_axis(t_vec3 w, t_vec3 *u, t_vec3	*v)
{
	w = normalize(w);
	if (w.y == 1 || w.y == -1)
		*u = create_vec3(w.y, 0, 0);
	else
		*u = cross(create_vec3(0, 1, 0), w);
	*v = cross(w, *u);
}

• cam의 axis는 z축부터 정한다. 레이트레이싱에서는 카메라가 위치한 곳에서 z축의 음의 방향에 뷰포트가 세팅된다.
• 따라서 w벡터를 파싱한 cam의 normal vector를 음수로 바꿔준 값으로 정한다.
• 이후 u, v axis 즉 x, y 축을 차례대로 구해준다.
• u axis는 먼저 0,1,0 벡터와 cross product를 하여 수직인 벡터를 구해준다. 이 때 w axis가 이미 0,1,0 또는 0,-1,0인 경우 수직 벡터를 제대로 구할 수 없기 때문에 그 땐 임의로 해당 벡터의 수직 벡터인 1,0,0 또는 -1,0,0 벡터로 세팅해줬다.
• v axis는 이제 w와 u를 cross product한 벡터로 설정 해주면 된다.
  

lower left corner

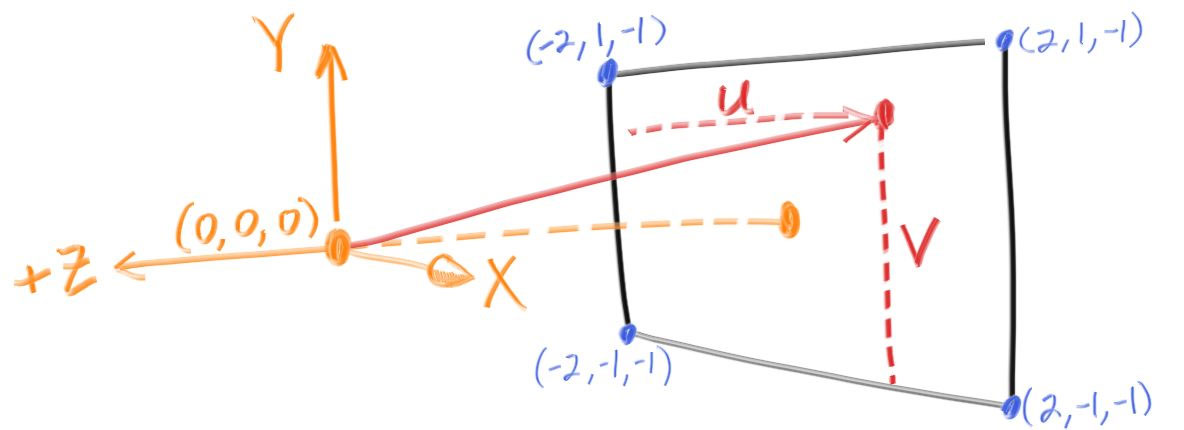
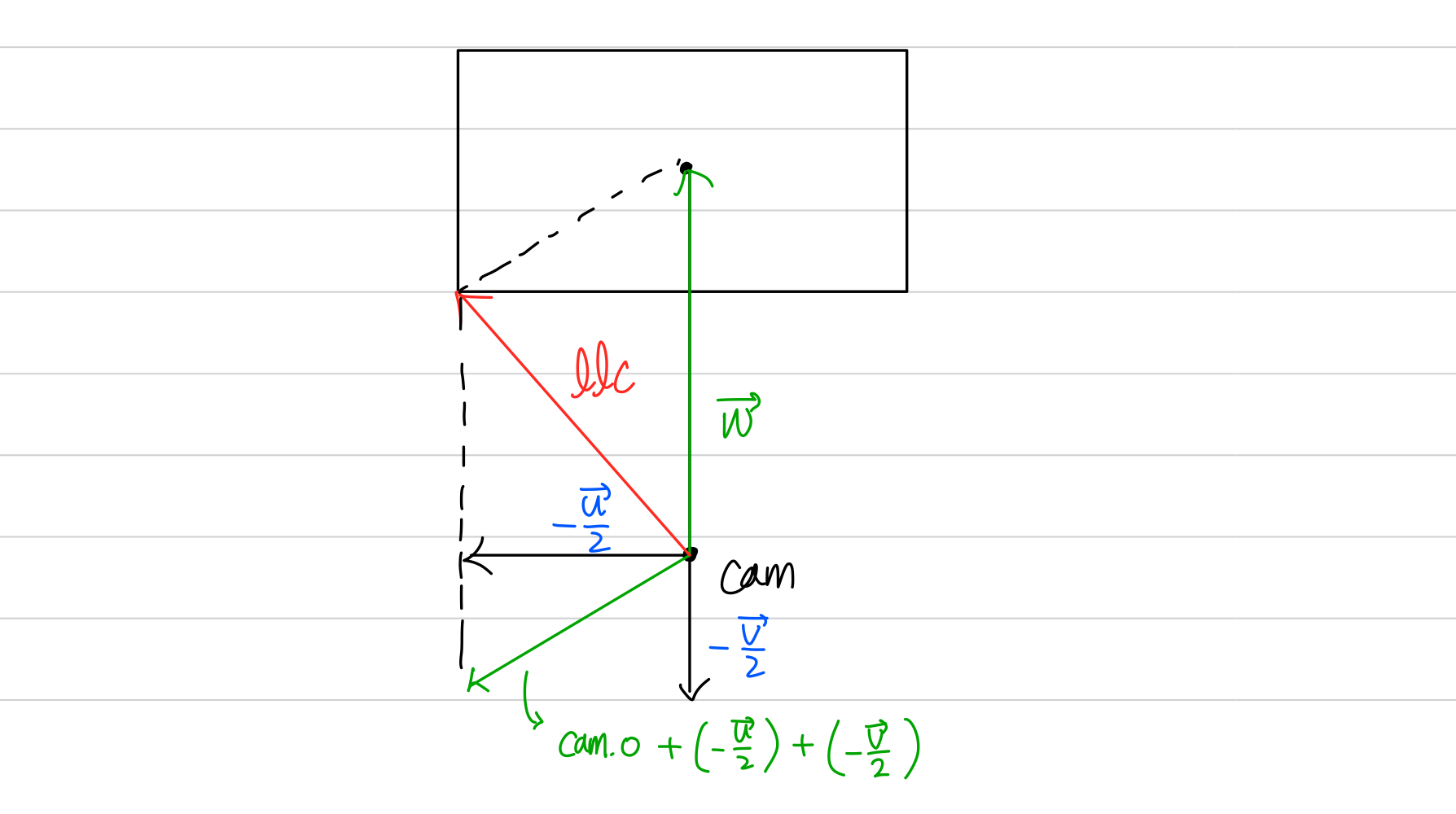
• cam의 축 설정이 끝나고 나면 ray를 쏠 시작점 lower left corner를 구해야 한다.
• lower left corner는 그림과 같이 cam origin을 기준으로 -u/2 벡터와 -v/2 벡터를 더한 벡터와 cam에서 뷰포트로 가는 w 벡터를 더해준 벡터가 된다.
  

Ray

ray = origin + (t * dir)

• ray는 ray가 시작되는 원점 origin에 방향벡터 direction에 시간 t를 곱한 값을 더하여 계산하게 된다.
• ray와 각 오브젝트의 교차점을 구하기 위한 방정식을 t에 대한 방정식으로 만들 수 있고, 방정식의 해를 구하고 해당 교점에서의 노멀벡터에 따라 표면처리를 해주는 식으로 색상이 정해지게 된다.

Object Intersection

plane

• https://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-plane-and-ray-disk-intersection

double	hit_plane_time(t_ray ray, t_plane pl)
{
	double	denom;
	double	time;

	denom = dot(pl.nv, ray.dir);
	if (denom == 0)
		return (INFINITY);
	time = (dot(pl.nv, vsub(pl.p, ray.o))) / denom;
	if (time <= EPSILON)
		return (INFINITY);
	return (time);
}

• t에 대한 일차방정식으로 풀 수 있다.
• 부동소수점의 오차 때문에 EPSILON 값을 적절히 사용해 결과값을 수정해준다.

int	hit_plane(t_ray *ray, t_figures elem)
{
	double	time;
	t_plane	pl;

	pl = elem.fig.pl;
	time = hit_plane_time(*ray, pl);
	if (ray->hit.time > time)
	{
		ray->hit.time = time;
		ray->hit.point = get_hit_point(*ray);
		if (dot(ray->dir, pl.nv) > 0) // dot = |dir| * |nv| * cos(θ)
			pl.nv = vscale(pl.nv, -1);
		ray->hit.nv = pl.nv;
		ray->hit.elem = elem;
		return (1);
	}
	return (0);
}

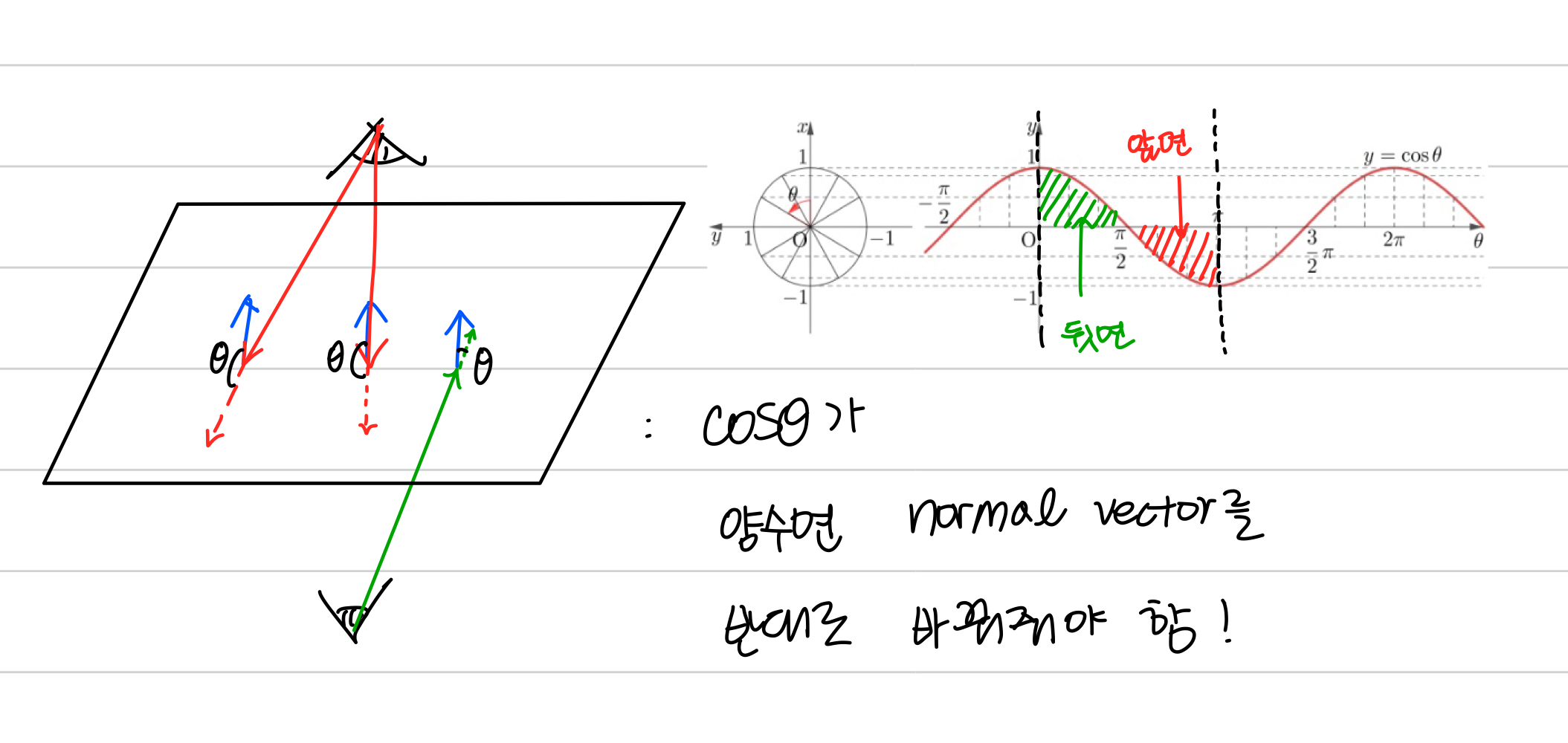
• plane과의 교점에서의 normal vector는 해당 plane의 normal vector를 그대로 넣어주면 된다.
• 대신 plane의 밑면쪽으로 가는 경우 cosine(θ) 값이 양수가 되는데, 이 때는 normal 벡터의 방향을 반대로 하여 넣어줘야 한다.
  

sphere

• https://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-sphere-intersection

int	hit_sphere(t_ray *ray, t_figures elem)
{
	t_vec3		oc;
	t_sphere	sp;
	double		time[2];

	sp = elem.fig.sp;
	oc = vsub(ray->o, sp.c);
	solve_quadratic(length_squared(ray->dir), 2 * dot(ray->dir, oc),
		length_squared(oc) - pow(sp.r, 2), time);
	if (ray->hit.time > time[0])
	{
		ray->hit.time = time[0];
		ray->hit.point = get_hit_point(*ray);
		ray->hit.nv = normalize(vsub(ray->hit.point, sp.c));
		ray->hit.elem = elem;
		return (1);
	}
	return (0);
}

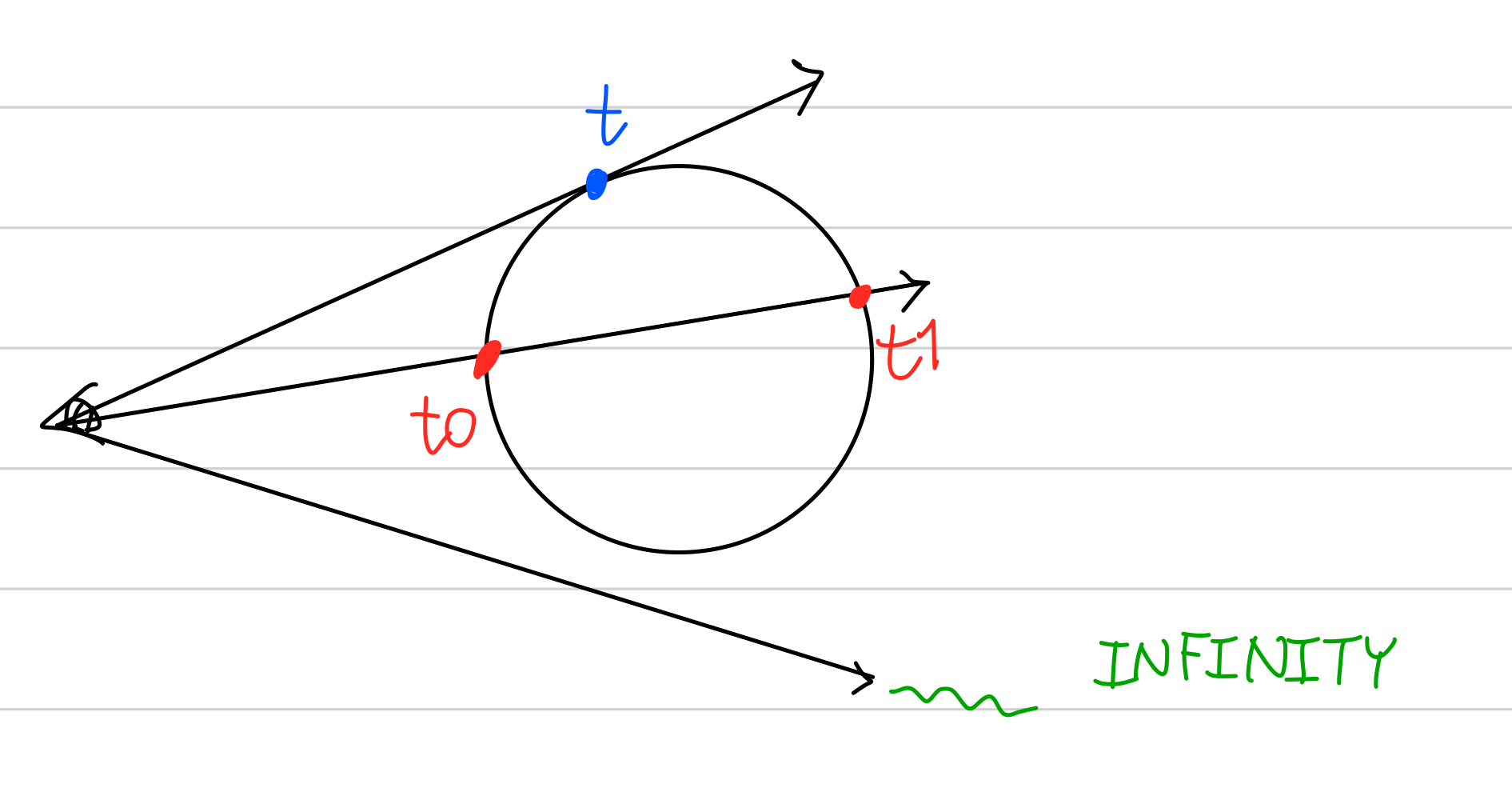
• t에 대한 이차방정식으로 풀 수 있다.
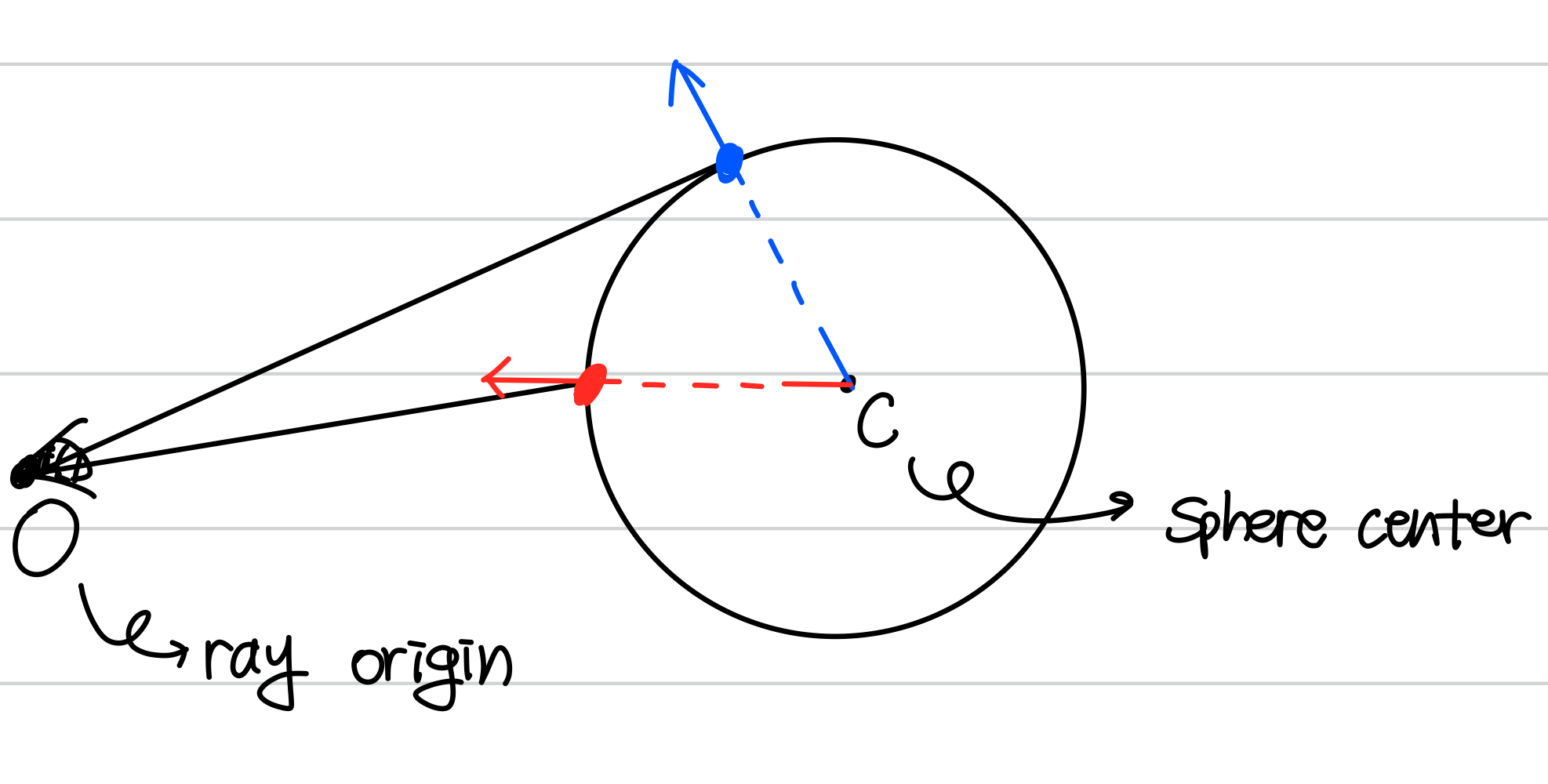
• 서로 다른 두 실근이 나오는 경우 먼저 부딪힌 곳(time의 값이 더 작은 좌표)의 색상이 찍혀야 한다.
• normal vector는 sphere의 center에서 교차점 P로 가는 벡터를 정규화 한 벡터가 된다. normalize($\overrightarrow{CP}$)

cylinder

• https://www.cl.cam.ac.uk/teaching/1999/AGraphHCI/SMAG/node2.html

double	hit_cylinder_time(t_ray ray, t_cylinder cy, double *y)
{
	t_vec3		v[2];
	t_vec3		oc;
	double		dist[2];
	double		time[2];

	oc = vsub(ray.o, cy.c);
	v[0] = vsub(ray.dir, vscale(cy.nv, dot(ray.dir, cy.nv)));
	v[1] = vsub(oc, vscale(cy.nv, dot(oc, cy.nv)));
	solve_quadratic(length_squared(v[0]),
		2 * dot(v[0], v[1]), length_squared(v[1]) - pow(cy.r, 2), time);
	dist[0] = dot(cy.nv, vsub(vscale(ray.dir, time[0]), vscale(oc, -1)));
	dist[1] = dot(cy.nv, vsub(vscale(ray.dir, time[1]), vscale(oc, -1)));
	if (dist[0] >= 0 && dist[0] <= cy.height)
	{
		*y = dist[0];
		return (time[0]);
	}
	if (dist[1] >= 0 && dist[1] <= cy.height)
	{
		*y = dist[1];
		return (time[1]);
	}
	return (INFINITY);
}

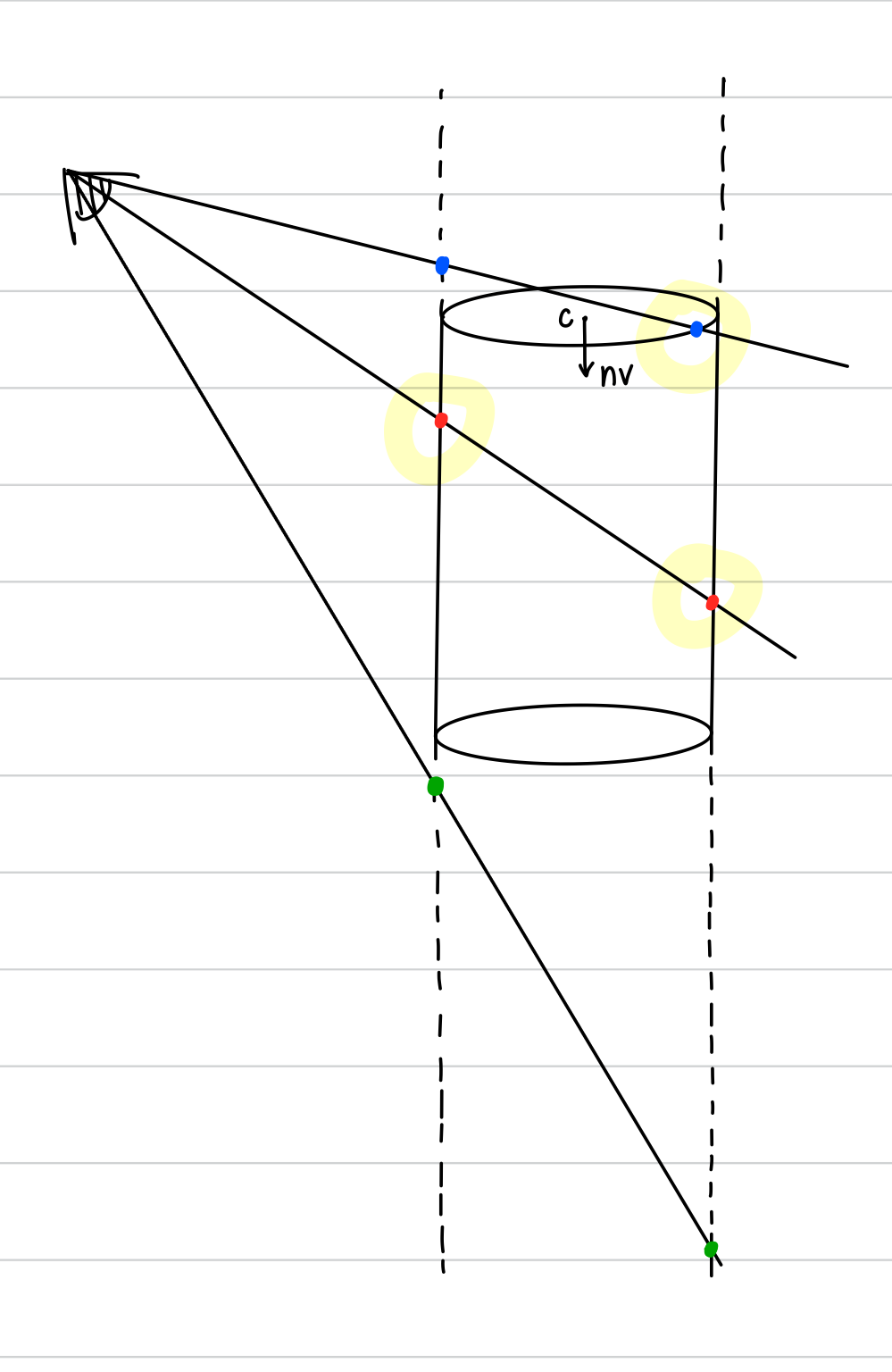
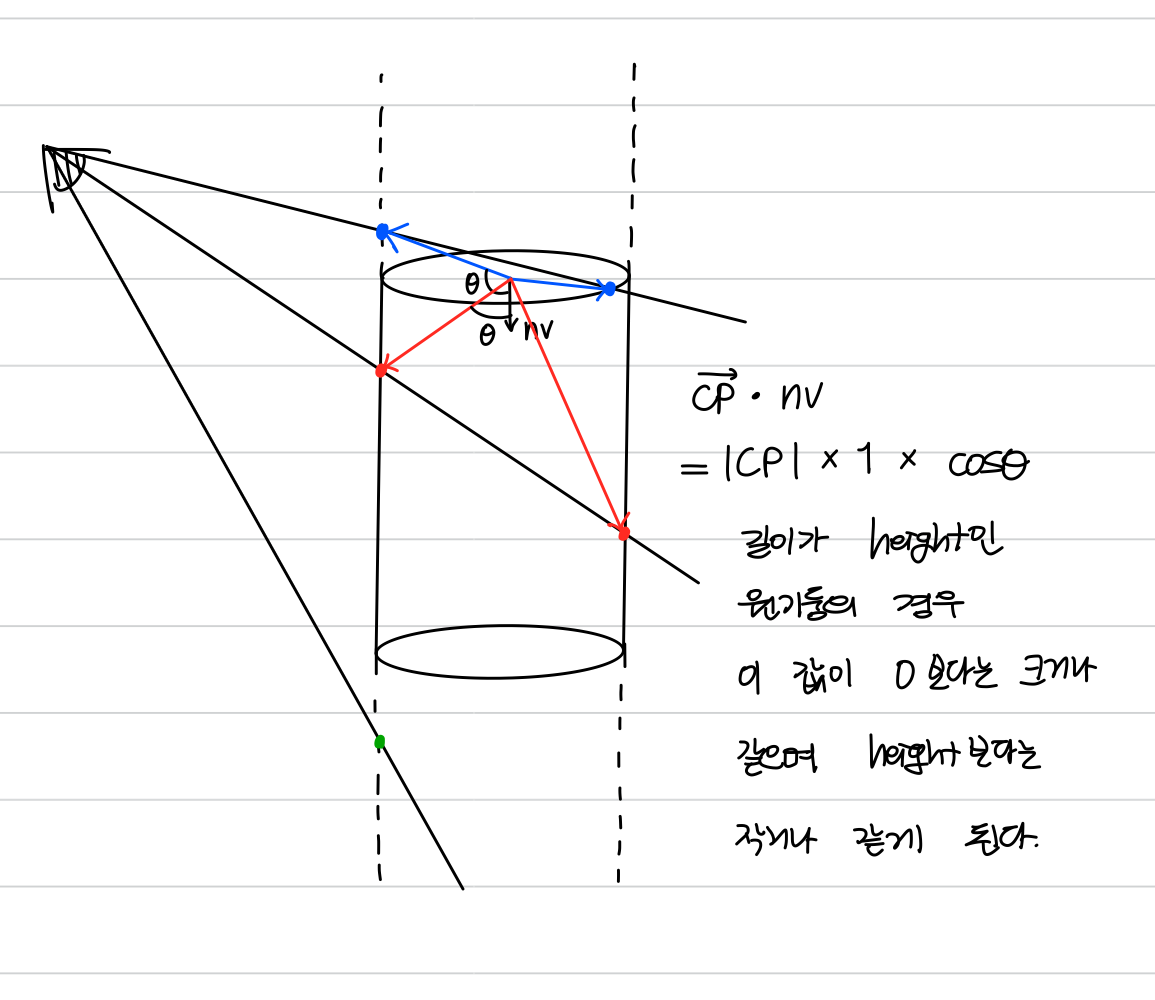
• cylinder 또한 t에 대한 이차방정식으로 해를 구해준다.
• 이 때 sphere와 다르게 무조건 작은 t값을 선택하면 안 되는데, cylinder의 해를 구하는 이차방정식은 그림과 같이 무한한 실린더라고 가정했을 때의 교차점이 구해지게 되기 때문이다.
• 때문에 cylinder의 중점 C에서 교차점 P로 가는 $\overrightarrow{CP}$ 와 normal vector를 dot product 한 값, 즉 정사영한 값이 0 <= x <= height 를 만족하는 경우에만 실근으로 인정한다.
• 만족하는 해가 하나인 경우 해당 값을 사용하면 되고
• 만족하는 해가 두 개가 나오는 경우 더 작은 값을 사용하면 되고
• 만족하는 해가 없는 경우 INFINITY로 처리한다.

int	hit_cylinder(t_ray *ray, t_figures elem)
{
	double		time;
	double		y;
	t_cylinder	cy;

	cy = elem.fig.cy;
	time = hit_cylinder_time(*ray, cy, &y);
	if (time < INFINITY && ray->hit.time > time)
	{
		ray->hit.time = time;
		ray->hit.point = get_hit_point(*ray);
		ray->hit.nv = normalize(vsub(ray->hit.point,
					vadd(vscale(cy.nv, y), cy.c)));
		ray->hit.elem = elem;
		return (1);
	}
	return (0);
}

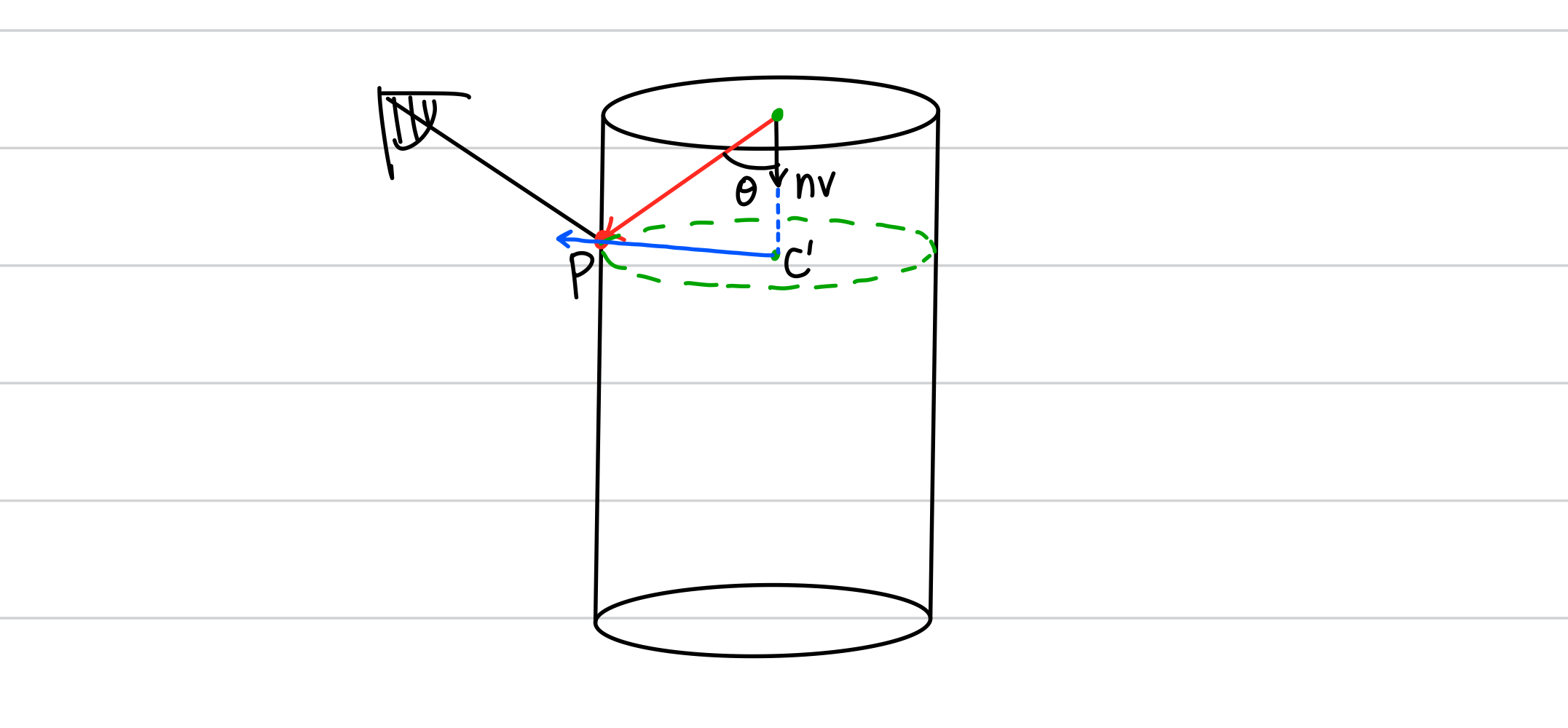
• cylinder의 normal vector는 이전의 해에서 구했던 P를 normal vector에 정사영 시킨 y를 이용한다.
• P가 위치한 실린더 단면에 생기는 원의 중심에서 교점 P로 향하는 벡터를 정규화 한 벡터가 된다. normalize($\overrightarrow{C'P}$)
  

cone

• https://lousodrome.net/blog/light/2017/01/03/intersection-of-a-ray-and-a-cone/

double	hit_cone_time(t_ray ray, t_cone con, double *cosine)
{
	t_vec3		oc;
	double		time[2];
	double		dist[2];

	oc = vsub(ray.o, con.c);
	*cosine = cos(con.theta / 2 * M_PI / 180);
	solve_quadratic(pow(dot(ray.dir, con.nv), 2) - pow(*cosine, 2),
		2 * (dot(ray.dir, con.nv) * dot(oc, con.nv)
			- dot(ray.dir, oc) * pow(*cosine, 2)),
		pow(dot(oc, con.nv), 2) - length_squared(oc) * pow(*cosine, 2),
		time);
	dist[0] = dot(con.nv, vsub(vscale(ray.dir, time[0]), vscale(oc, -1)));
	dist[1] = dot(con.nv, vsub(vscale(ray.dir, time[1]), vscale(oc, -1)));
	if (dist[0] >= 0 && dist[0] <= con.height)
		return (time[0]);
	if (dist[1] >= 0 && dist[1] <= con.height)
		return (time[1]);
	return (INFINITY);
}

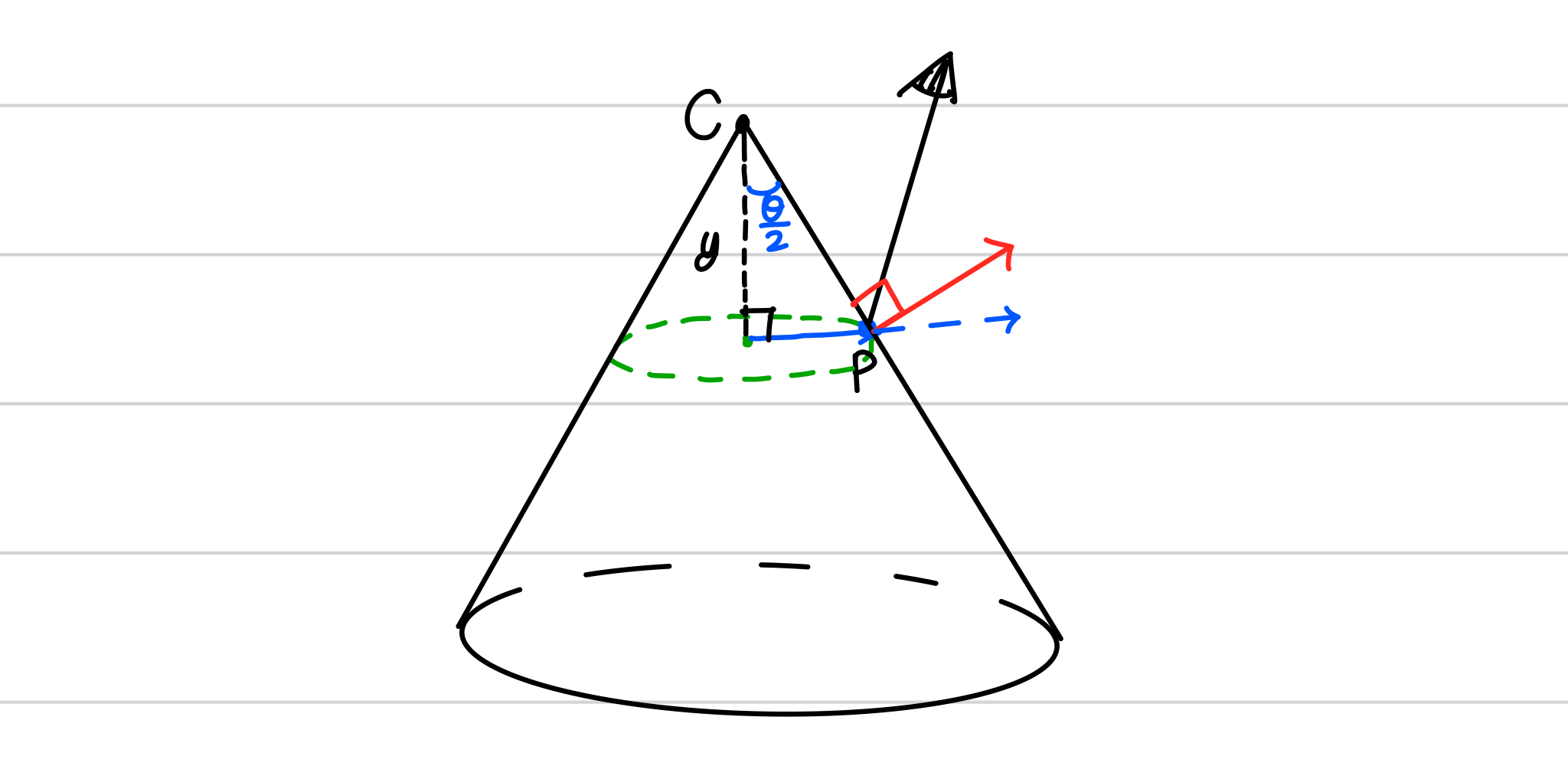
• cone도 cylinder와 비슷하다.
• t에 대한 이차방정식을 풀고
• 해당 교차점 P에 대한 ray를 nv에 정사영시켰을 때 0 ~ height 사이 값을 가져야만 실근이라고 인정한다.

int	hit_cone(t_ray *ray, t_figures elem)
{
	double		time;
	double		cosine;
	t_cone		con;
	t_vec3		cp;

	con = elem.fig.con;
	time = hit_cone_time(*ray, con, &cosine);
	if (ray->hit.time > time)
	{
		ray->hit.time = time;
		ray->hit.point = get_hit_point(*ray);
		cp = vsub(ray->hit.point, con.c);
		ray->hit.nv = normalize(vsub(vscale(normalize(cp), cosine), con.nv));
		ray->hit.elem = elem;
		return (1);
	}
	return (0);
}

• normal vector는 normalize($\overrightarrow{CP}$)에 cosine(θ)를 곱한 벡터에서 con의 normal vector를 뺀 벡터로 구해준다.
  

Phong model

• https://cuca.tistory.com/entry/주변광ambient-분산광diffuse-반사광specular
• phong model은 ambient light, diffuse, specular reflection이 합쳐진 모델이다.

ambient light

• 주변광
• 특정한 방향이 없이 주변을 덮고 있는 빛
• 여러 가지 요소들에 부딪히고 반사되어 점차 방향을 잃어버린 빛의 형태
• 미니알티에서는 파싱한 ambient light 색과 밝기를 곱해주어 ambient light을 정한다.

al_clr = cscale(rt->scene.al_clr, rt->scene.al_br);

diffuse light

• https://www.scratchapixel.com/lessons/3d-basic-rendering/phong-shader-BRDF
• ALBEDO x light brightness x cosine(θ)

double	diffuse(t_light light, t_ray ray)
{
	t_vec3		p_to_light;
	double		cos_with_light;

	p_to_light = vsub(light.o, ray.hit.point);
	cos_with_light = clamp(dot(normalize(p_to_light), ray.hit.nv), 0, 1);
	if (cos_with_light > 0)
		return (ALBEDO * light.br * cos_with_light);
	else
		return (0);
}

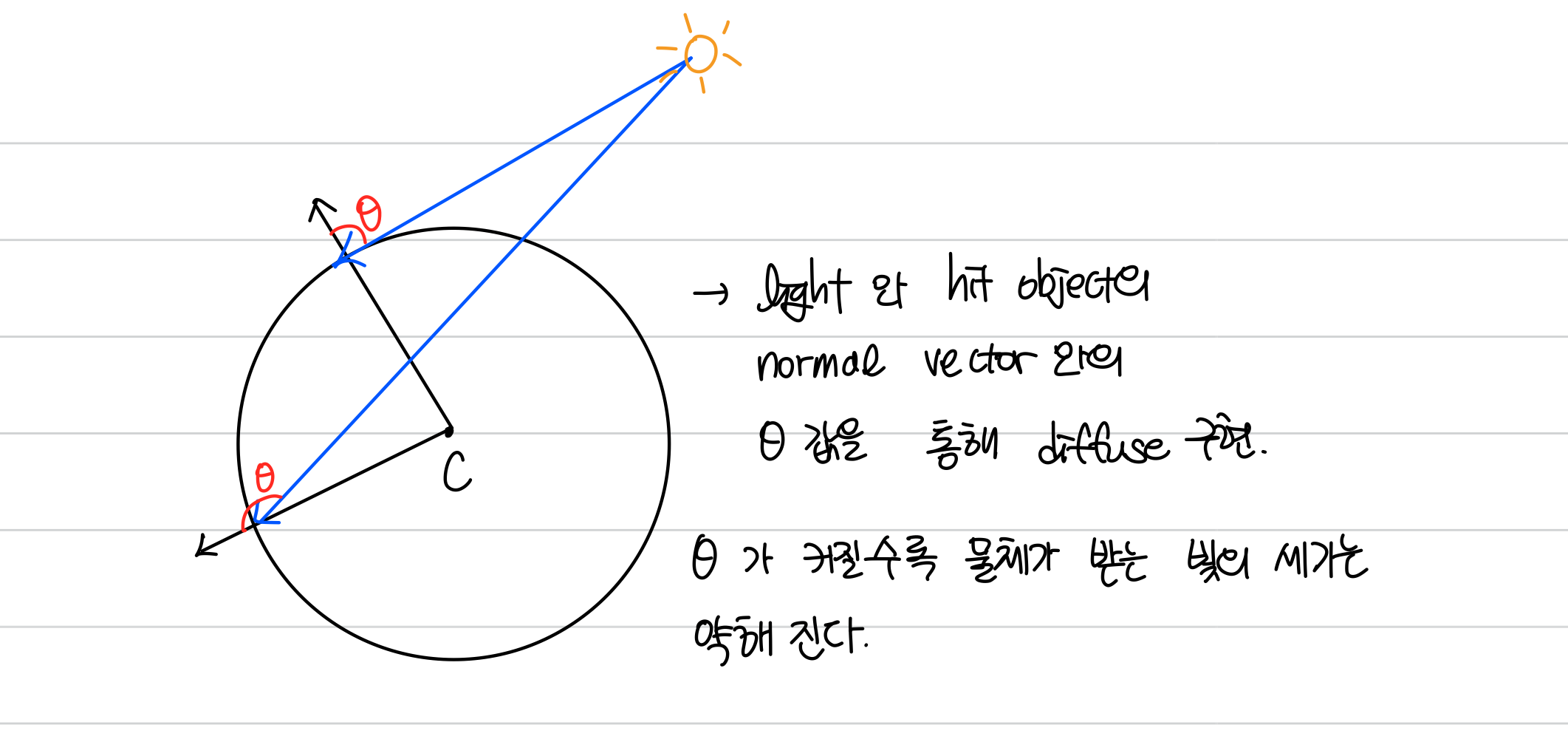
• 분산광
• 일정한 방향으로 빛이 들어와서 물체의 표면에서 여러 방향으로 분산되는 빛의 형태
• 분산되기는 하지만 이러한 빛을 받는 표면은 그렇지 않은 부분에 비해 밝게 보인다.
• hit한 object의 normal vector와 조명 벡터와의 각도를 가지고 diffuse reflection을 구현한다.
  

specular light

• https://www.scratchapixel.com/lessons/3d-basic-rendering/phong-shader-BRDF
• $(V · R)^n$

t_vec3	reflect_ray(t_vec3 p_to_light, t_vec3 hit_normal)
{
	return (vsub(vscale(hit_normal, 2 * dot(p_to_light, hit_normal)), \
					p_to_light));
}

double	specular(t_light light, t_ray ray)
{
	t_vec3	p_to_light;
	t_vec3	reflected;
	t_vec3	p_to_cam;
	double	scalar;

	p_to_light = vsub(light.o, ray.hit.point);
	reflected = reflect_ray(normalize(p_to_light), ray.hit.nv);
	p_to_cam = vscale(ray.dir, -1);
	scalar = dot(normalize(reflected), normalize(p_to_cam));
	if (ray.hit.elem.specular > 0 && scalar > 0)
		return (light.br * pow(scalar, ray.hit.elem.specular));
	else
		return (0);
}

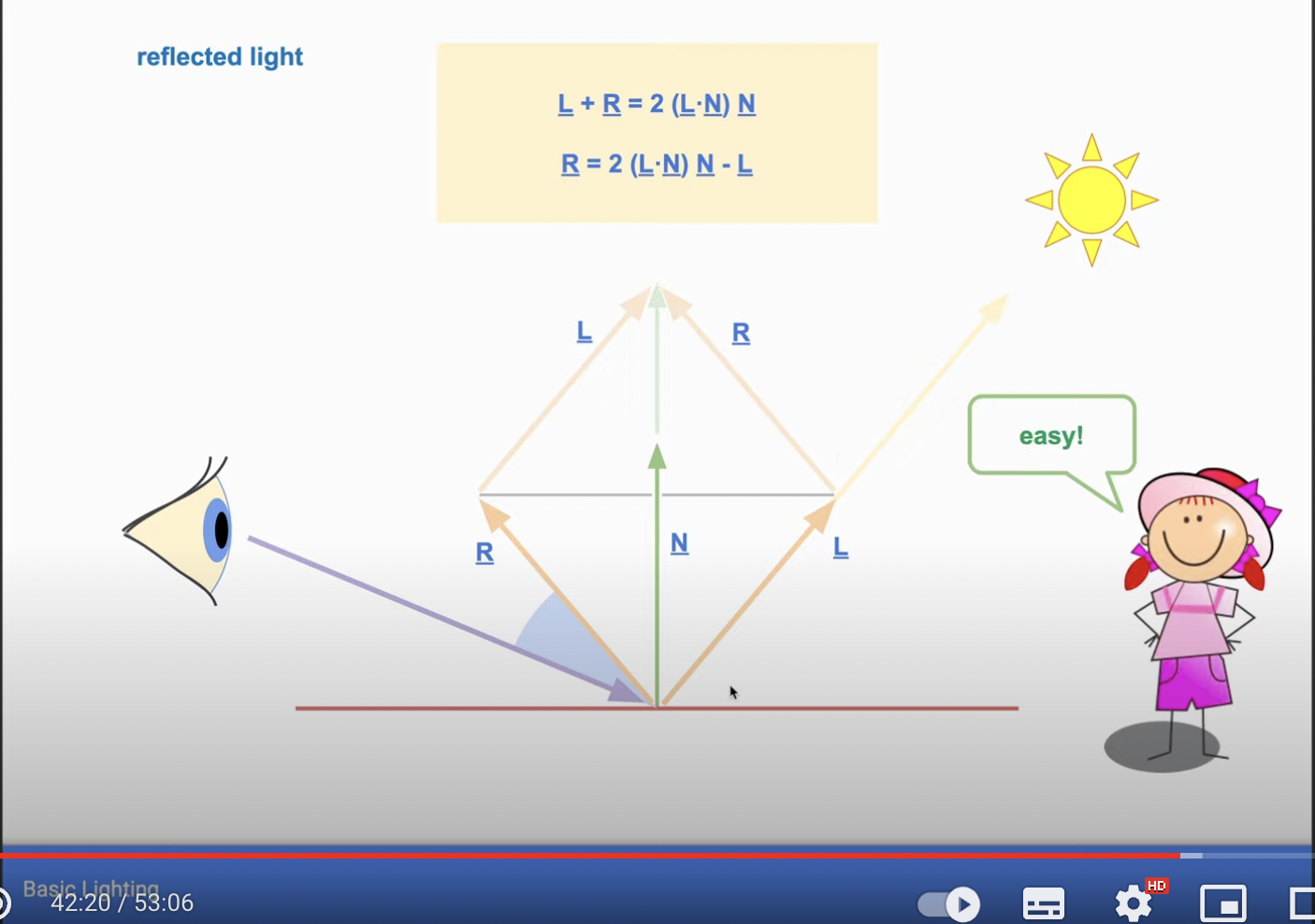
• 반사광
• 특정한 방향으로 유입되어 한 방향으로 완전히 반사되는 빛
• 강한 반사광은 물체 표면에 밝은 점을 형성하며, 이를 반사 하이라이트(highlight)라고 한다.
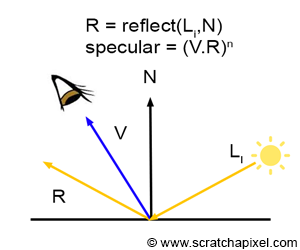
• specular reflection은 light의 reflected ray와 cam에서 오는 ray를 dot product한 값을 가지고 구해준다.
• reflected ray는 $R=2(N⋅L)N−L$ 로 구해줄 수 있다.

Shadow

int	in_shadow(t_minirt *rt, t_hit hit, t_light *light)
{
	t_ray	shadow;
	int		ret;

	shadow.o = hit.point;
	shadow.dir = normalize(vsub(light->o, hit.point));
	ret = intersect(rt, &shadow);
	if (distance(hit.point, light->o) <= distance(hit.point, shadow.hit.point))
		return (0);
	return (ret);
}

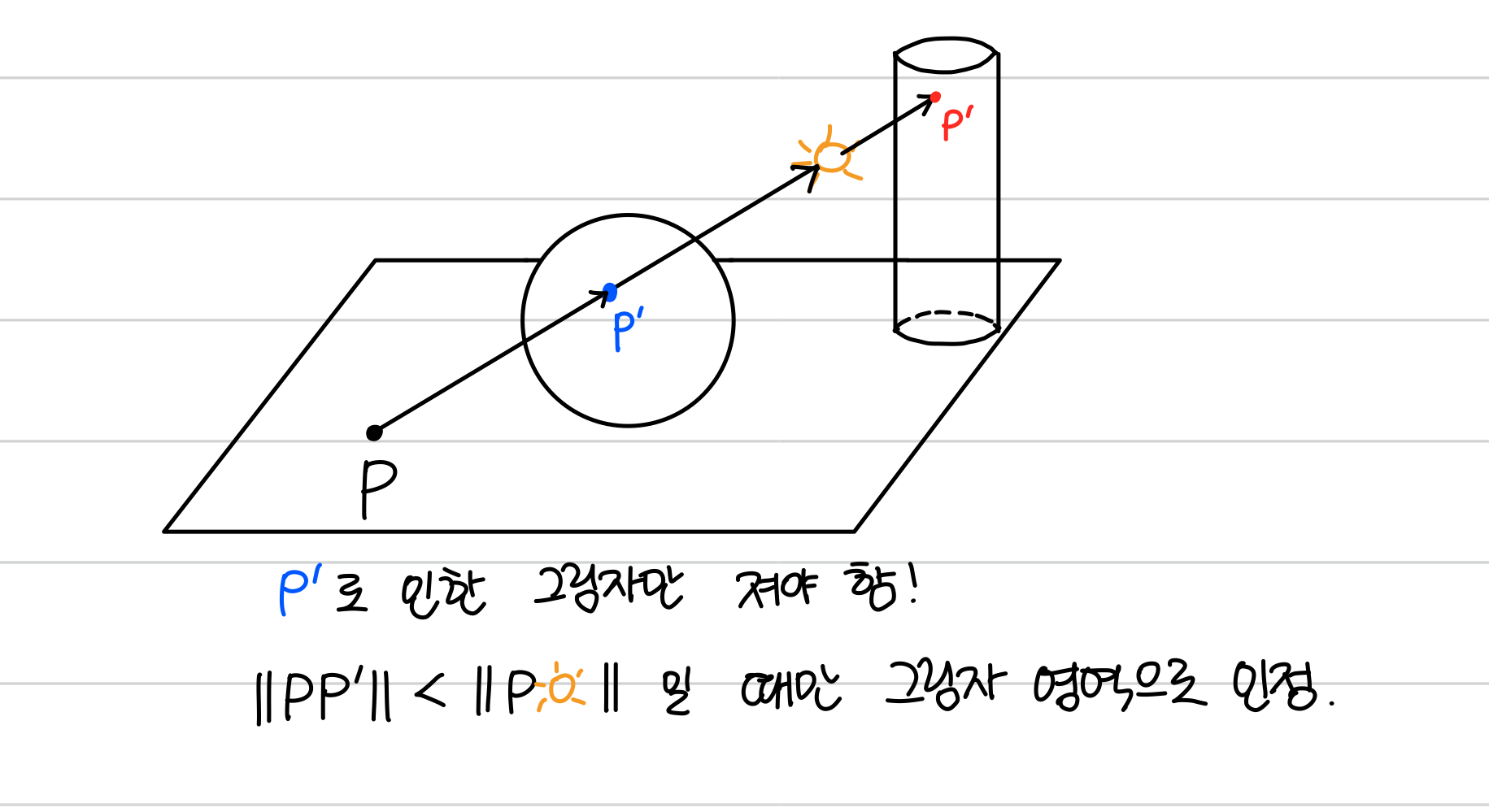
• hit point에서 다시 빛으로 가는 벡터를 쐈을 때 부딪히는 물체가 있다면, 해당 부분은 그림자가 져야 한다.
• 이 때 부딪히는 곳이 light 보다 더 멀리 있을 때는 유효하지 않다고 판단한다.
  

Texture mapping

uv mapping

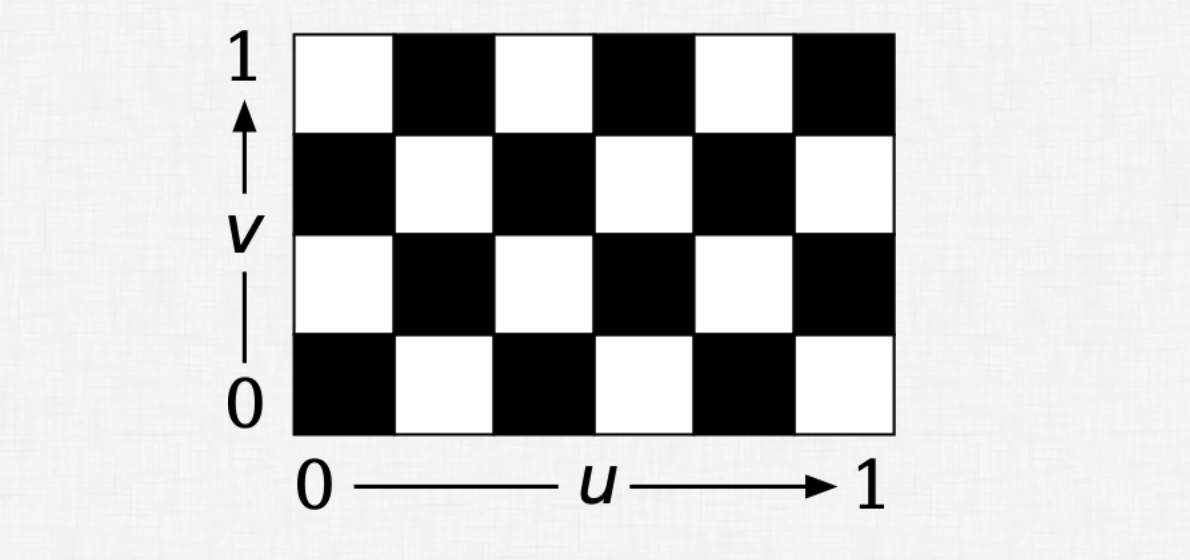
• 각 좌표계를 uv좌표계로 옮겨주면 된다.
• u와 v는 0~1 사이의 범위를 갖는다.

구면 좌표계

• https://ko.wikipedia.org/wiki/%EA%B5%AC%EB%A9%B4%EC%A2%8C%ED%91%9C%EA%B3%84

void	uv_mapping_sphere(double *u, double *v, t_vec3 uv_axis[2], t_hit hit)
{
	double	theta;
	double	phi;

	set_uv_axis(hit.nv, &uv_axis[0], &uv_axis[1]);
	theta = acos(-1 * hit.nv.y);
	phi = atan2(-1 * hit.nv.z, hit.nv.x) + M_PI;
	*u = phi * M_1_PI * 0.5;
	*v = theta * M_1_PI;
}

• 구의 경우 각도만을 가지고 매핑이 되기 때문에 1/π 또는 1/2π 를 곱해주어 0~1 사이의 값으로 맞춰 주면 된다.

원통 좌표계

• https://ko.wikipedia.org/wiki/%EC%9B%90%ED%86%B5%EC%A2%8C%ED%91%9C%EA%B3%84

void	uv_mapping_cylinder(double *u, double*v, t_vec3 uv_axis[2], t_hit hit)
{
	t_vec3	pc;
	double	theta;
	double	height;

	set_uv_axis(hit.elem.fig.cy.nv, &uv_axis[0], &uv_axis[1]);
	pc = vsub(hit.point, hit.elem.fig.cy.c);
	theta = atan2(-1 * dot(pc, uv_axis[0]), dot(pc, uv_axis[1])) + M_PI;
	height = dot(pc, hit.elem.fig.cy.nv);
	*u = theta * M_1_PI * 0.5;
	*v = height / hit.elem.fig.cy.height;
}

• 실린더의 경우 z를 실린더의 height으로 나누면 0~height 사이의 값이 0~1사이 값으로 적절히 매핑된다.

원뿔 좌표계

void	uv_mapping_cone(double *u, double *v, t_vec3 uv_axis[2], t_hit hit)
{
	t_vec3	pc;
	double	theta;
	double	height;

	set_uv_axis(hit.elem.fig.con.nv, &uv_axis[0], &uv_axis[1]);
	pc = vsub(hit.point, hit.elem.fig.con.c);
	theta = atan2(-1 * dot(pc, uv_axis[0]), dot(pc, uv_axis[1])) + M_PI;
	height = dot(pc, hit.elem.fig.con.nv);
	*u = theta * M_1_PI * 0.5;
	*v = height / hit.elem.fig.con.height;
}

• 원뿔 좌표계도 원통 좌표계와 같이 해주면 된다.

checker board

int	checker_board_pattern_at(double u, double v, t_hit hit)
{
	int	u2;
	int	v2;
	int	ret;

	u2 = u * hit.elem.checker_w;
	v2 = v * hit.elem.checker_h;
	ret = (u2 + v2) % 2;
    if (u * v < 0)
    	ret = !ret;
	if (ret)
		return (hit.elem.clr);
	else
		return (complementary_color(hit.elem.clr));
}

• http://raytracerchallenge.com/bonus/texture-mapping.html
• uv mapping을 했으니 checker board는 쉽다.
• 파싱할 때 받아온 checker board의 w, h를 가지고 각각을 u,v 값에 곱하고 내림한 값으로 원래 색을 찍을지, 보색을 찍을지 결정해주면 된다.
  

image mapping

int	image_mapping(double u, double v, t_xpm_img img_map)
{
	int		u2;
	int		v2;
	int		color;

	u2 = u * img_map.w;
	v2 = (1.0 - v) * img_map.h;
	color = get_pixel_color(img_map, u2, v2);
	return (color);
}

• 위에서 설정한 uv 좌표계를 통해 받아온 이미지의 픽셀값을 매칭시키면 된다.

normal mapping

t_vec3	normal_mapping(double u, double v, t_vec3 uv_axis[2], t_hit hit)
{
	int		u2;
	int		v2;
	int		color;
	t_vec3	normal_color;

	u2 = u * hit.elem.tx->bmp_map.w;
	v2 = (1.0 - v) * hit.elem.tx->bmp_map.h;
	color = get_pixel_color(hit.elem.tx->bmp_map, u2, v2);
	normal_color = color_to_vec3(color);
	normal_color = vsub(vscale(normal_color, 2), create_vec3(1, 1, 1));
	return (change_basis(uv_axis[0], uv_axis[1], hit.nv, normal_color));
}

• https://learnopengl.com/Advanced-Lighting/Normal-Mapping
• https://bbtarzan12.github.io/Noraml-Mapping/
• normal mapping에 사용할 이미지는 해당 점에서의 법선벡터 값을 r,g,b 값으로 담고 있다.
• 대신 이 값이 tangent space에서의 값으로 되어 있기 때문에 tangent space에서 원래 좌표계의 기저로 변환하는 작업이 필요하다.

t_vec3	change_basis(t_vec3 v1, t_vec3 v2, t_vec3 v3, t_vec3 vec)
{
	t_vec3	normal;

	normal.x = v1.x * vec.x + v2.x * vec.y + v3.x * vec.z;
	normal.y = v1.y * vec.x + v2.y * vec.y + v3.y * vec.z;
	normal.z = v1.z * vec.x + v2.z * vec.y + v3.z * vec.z;
	return (normal);
}

• 변환을 하고 나면 원래 매끈한 표면일 때의 법선벡터에서 표면 처리가 된 법선벡터로 연산되기 때문에 그래픽이 달라지게 된다.