[CS] 자료구조: 해시 테이블, 힙

해시 테이블 (Hash Table)

다양한 데이터를 효율적으로 관리하기 위해 사용되는 자료구조. 해싱 과정을 통해 데이터를 빠르고 효울적으로 저장하고 검색. 큰 범위를 가진 데이터들을 해싱을 통해 한정된 범위의 정수값을 가진 해시로 만들고, 해시라는 키들에 원본 데이터들을 매핑시켜놓은 테이블

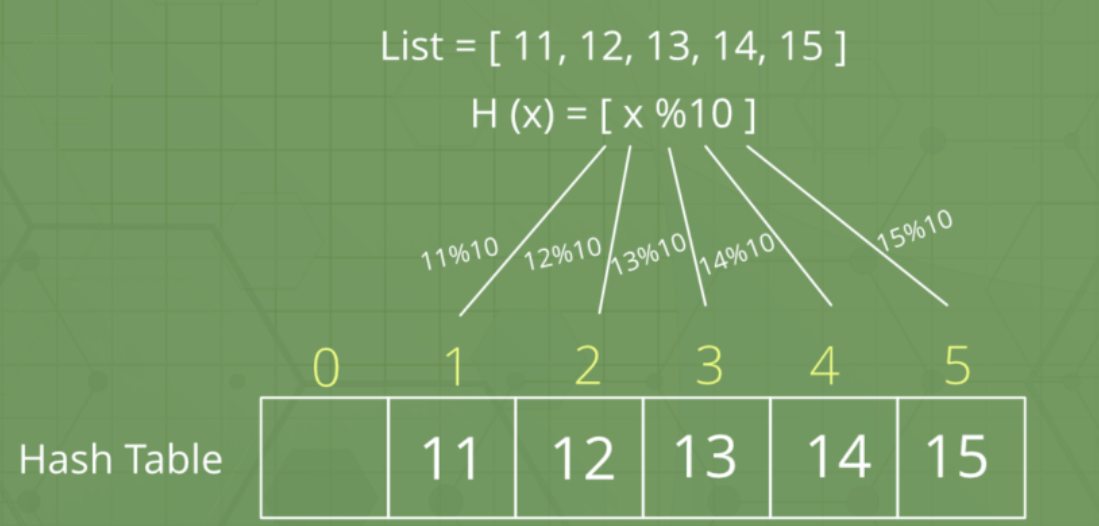
1. 해시, 해싱, 해시함수

• 해시 : 다양한 길이를 가진 데이터를 고정된 길이의 데이터로 변환한 값
• 해싱 : 데이터를 해시로 변환하는 과정. 해시 함수에 의해 수행됨
• 해시함수: 임의의 데이터를 일정한 길이의 데이터로 변환하는 함수

2. 해시 함수 예제

• % 연산자를 사용하여 데이터를 0~19 사이의 해시로 변환

import java.util.Arrays;

public class HashExample {
    public static void main(String[] args) {
        int[] a = {1, 2, 42, 4, 12, 14, 17, 13, 37};
        for (int i = 0; i < a.length; i++) {
            a[i] = hashFunction(a[i]);
        }
        System.out.println(Arrays.toString(a));
    }

    public static int hashFunction(int num) {
        return num % 20;
    }
}

• 문자열을 숫자로 해싱하는 방법도 존재 (아스키 코드 사용)
  • str.toCharArray()로 숫자로 변환한 뒤, 해시 함수 적용
  • A = 65, a = 97

 public static int hashFunction(String str, int size) {
        int hash = 3;
        for (char c : str.toCharArray()) {
            hash *= (int) c;
            hash %= size;
        }
        return hash;
    }

• 해시는 db에 개인정보를 암호화하여 저장할 때 사용되기도 한다 (대표적인 해시 알고리즘: bcrypt 비크립트, MD5)

3. 해시 테이블의 시간 복잡도

최악의 시간 복잡도와 평균 시간 복잡도의 차이가 크다

• 평균 시간 복잡도: O(1) 대부분의 경우 빠른 참조, 탐색, 삽입, 삭제 가능
• 최악 시간 복잡도: O(n) 해시 충돌이 많이 발생할 경우 참조, 탐색, 삽입, 삭제 시간 증가

4. 해시 테이블에서의 충돌(collision) 해결

체이닝(Chaining)

• 충돌이 발생하면 연결리스트에 데이터를 저장
• 이때 연결 리스트 뿐만 아니라, 동적 배열, 균형잡힌 트리인 레드 블랙 트리가 사용되며, java 8 이상에서는 요소의 수가 특정 임계값을 넘어가면 연결리스트가 아닌 레드 블랙트리를 해시 map에 사용하여 O(n)의 시간 복잡도를 O(logn)으로 개선
  

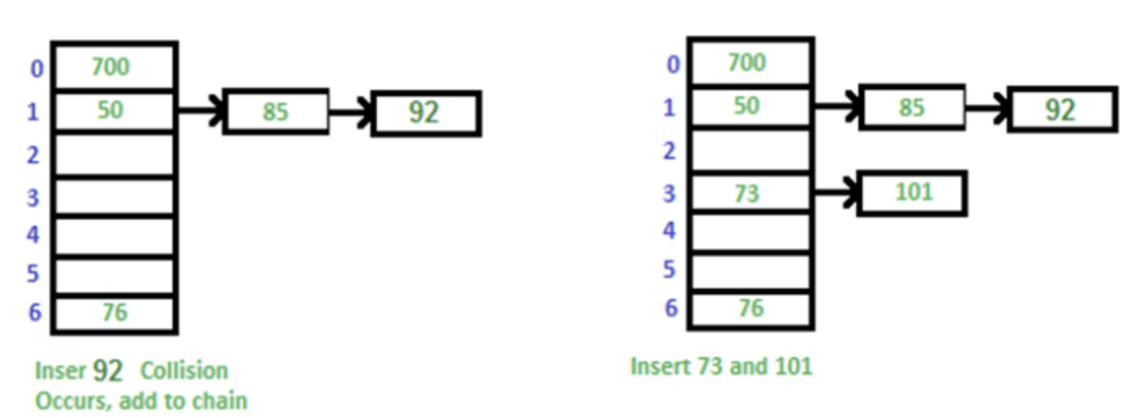
개방 주소법(Open Addressing)

• 충돌이 발생하면 다른 버켓에 데이터를 저장
  • 선형 탐색: 해시 충돌 시 다음 또는 몇 개 선형적으로 건너뛴 버켓에 데이터를 삽입
  • 제곱 탐색 : 1, 4, 9, 16.. 번째 뒤 버켓에 데이터 삽입
  • 이중 해싱: 해시 함수 한 번 더 적용한 결과를 사용해서 데이터 삽입

힙 (Heap)

최대/최솟값을 빠르게 찾는 자료구조. 완전이진트리(왼쪽부터 채워진 트리) 기반의 자료구조

1. 힙의 종류

• 최대힙(Max Heap): 부모 노드가 자식 노드보다 항상 크거나 같음
• 최소힙(Min Heap): 부모 노드가 자식 노드보다 항상 작거나 같음

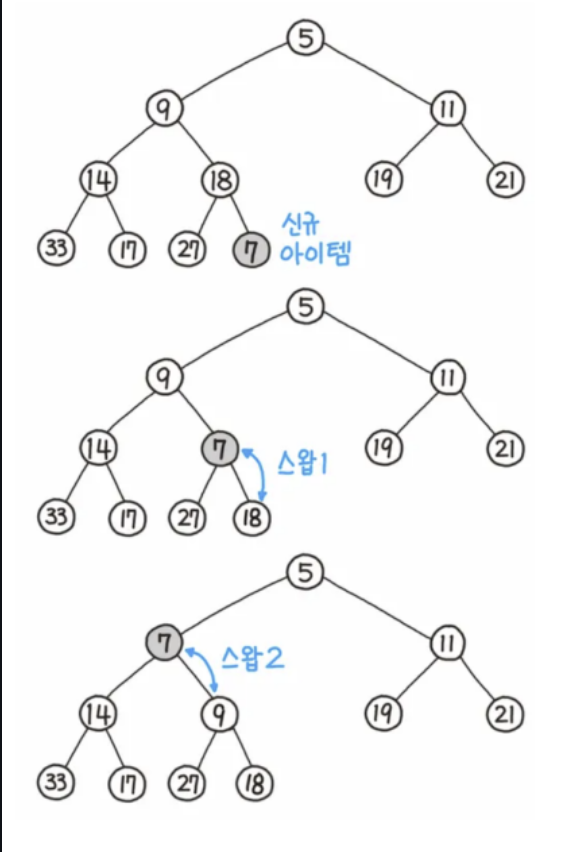
2. 힙의 데이터 삽입 및 삭제

• 힙의 데이터 삽입

1. 리프노드에 삽입할 노드를 삽입한다
2. 해당 노드와 부모노드를 서로 비교한다
3. 규칙에 맞으면 그대로 두고, 그렇지 않으면 부모 노드와 교환한다 (규칙 : 최대힙|최소힙)
4. 규칙에 맞을 때까지 3번 과정을 반복한다

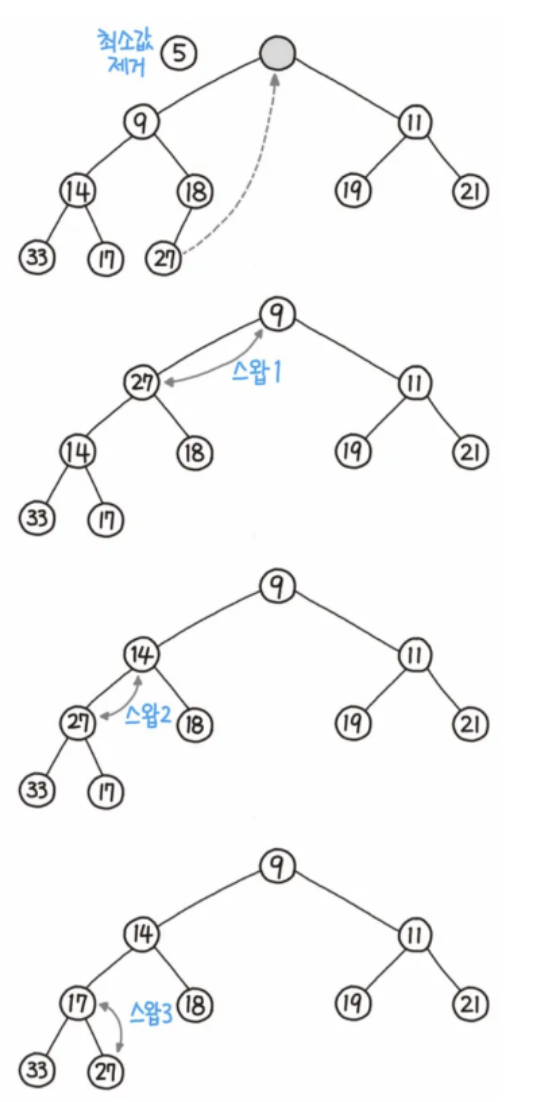
• 힙의 데이터 삭제

1. 루트 노드를 제거
2. 루트 자리에 가장 마지막 노드를 삽입한다
3. 올라간 노드와 그의 자식 노드를 비교한다
4. 규칙을 만족하면 그대로 두고, 그렇지 않으면 자식 노드와 교환한다

3. 이진 탐색 트리와의 차이점

• 이진 탐색 트리는 정렬된 순서로 데이터를 저장하는 반면, 힙은 최대값이나 최솟값에 빠르게 접근할 수 있도록 구성
• 이진 탐색 트리는 탐색에 유리하지만, 힙은 삽입과 삭제에 더 효율적

4. 힙의 시간 복잡도

• 참조: O(1), 루트 노드에 접근하는데 걸리는 시간
• 탐색: O(n), 모든 노드를 탐색해야 알 수 있음
• 삽입/삭제: O(logn), 힙을 재조정하는데 걸리는 시간

---

REF