[CS] 그래프를 표현하는 2가지 방법: 인접 행렬과 인접 리스트

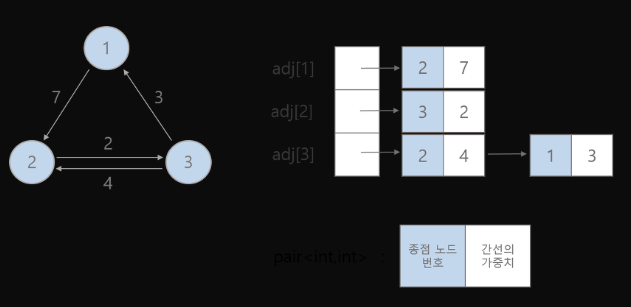
인접 행렬과 인접리스트는 그래프를 표현하는 2가지 주요 방법. 둘 다 그래프의 정점들과 간선을 나타내는데 사용되지만, 방식과 성능 면에서 차이가 존재

인접행렬 (Adjacency Matrix)

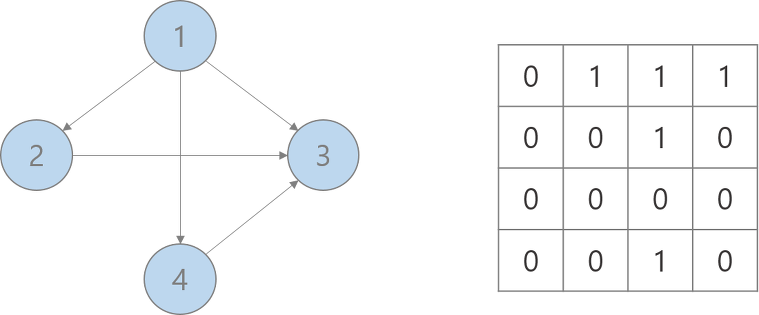
1. 정의

• 정점과 정점 사이의 연결 관계를 이차원 배열로 표현

2. 공간 복잡도

• O(V^2) 정점의 수 V의 제곱에 비례하는 메모리가 필요

3. 특징

• 각 셀 (i,j)는 정점 i와 정점 j 사이에 간선이 있으면 1(또는 가중치) , 없으면 0으로 표시됨
• 자기 자신으로의 연결은 행렬의 대각선에 위치하며 , 사이클의 유무에 따라 값이 표시된다
• 무방향 그래프의 경우, 행렬은 대칭적

4. 시간 복잡도

• 특정 간선의 존재 여부 확인: O(1)
• 모든 간선 순회: O(V^2)

인접 리스트(Adjacency List)

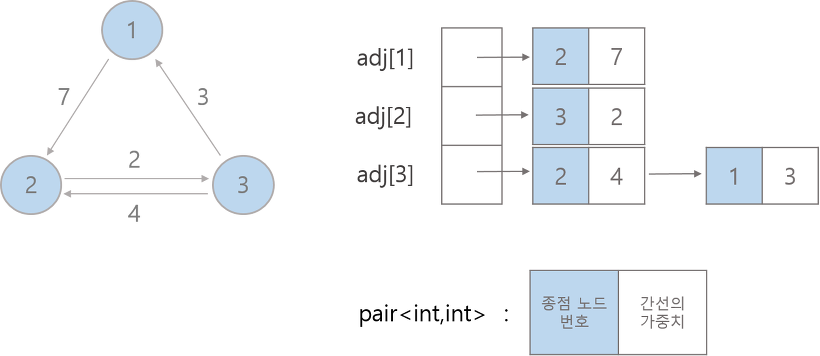
1. 정의

• 각 정점에 연결된 다른 정점의 목록을 배열이나 리스트로 표현

2. 공간 복잡도

• O(V+E) : 정점의 수 V와 간선의 수 E의 합에 비례하는 메모리가 필요

3. 특징

• 각 정점마다 해당 정점에서 출발하는 간선의 목록을 저장
• 연결된 정점들의 순서는 그래프의 특성에 따라 다를 수 있음
• 무방향 그래프의 경우 각 간선은 2번 저장됨

4. 시간 복잡도

• 특정 간선의 존재 여부 확인: 최악의 경우 O(V)
• 모든 간선 순회: O(V+E)

인접행렬과 인접 리스트의 차이점 및 선택 기준

1. 메모리 사용

• 인접 리스트는 인접 행렬에 비해 일반적으로 적은 메모리 사용. 특히 그래프가 희소(sparse) 한 경우. 반면, 그래프가 조밀(dense) 한 경우, 특히 간선의 수가 많으면 인접 행렬의 메모리 사용이 더 효율적일 수 있다

2. 속도

• 인접 행렬은 특정 간선의 존재 여부를 O(1) 만에 확인할 수 있지만, 모든 간선을 순회하는데는 O(V^2)이 걸린다. 반면 인접 리스트는 간선의 존재 여부를 확인하는데 더 많은 시간이 필요하지만 모든 간선을 순회하는데는 O(V+E)의 시간만 걸림

3. 실용성

• 실제 코딩에서는 대부분의 그래프가 희소하기 때문에 인접 리스트의 사용이 더 많다.

---

REF