[코딩테스트] 1, 2, 3 더하기 4 (DP)

문제

정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 4가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다. 합을 이루고 있는 수의 순서만 다른 것은 같은 것으로 친다.

1+1+1+1
2+1+1 (1+1+2, 1+2+1)
2+2
1+3 (3+1)

정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 10,000보다 작거나 같다.

출력

각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.

예제 입력 1

3
4
7
10

예제 출력 1

4
8
14

생각

• 만약에 합을 이루고 있는 수의 순서가 다른 것을 다른 것으로 친다면, 이는 DP로 아주 간단하게 풀 수 있는 문제이다 dp[n] = dp[n-1] + dp[n-2] + dp[n-3]
• 하지만 수의 순서만 다른 것을 같은 것으로 여기기 때문에, DP로 풀 때 3가지 경우로 나누어서 구해보았다. 현재 숫자 n보다 1 작을 때 1 중복 없이 더하는 경우, n 보다 2 작을 때 2를 중복 없이 더하는 경우, n보다 3 작을 때 3을 중복 없이 더하는 경우를 아래 표와 같이 나누어 구하였고, 점화식도 구해보았다!
• 마지막에 return할 때는 3가지 경우의 수를 모두 더해서 return하였다.

dp[n][k] = n을 만들기 위해서 k를 마지막으로 더하는 경우의 수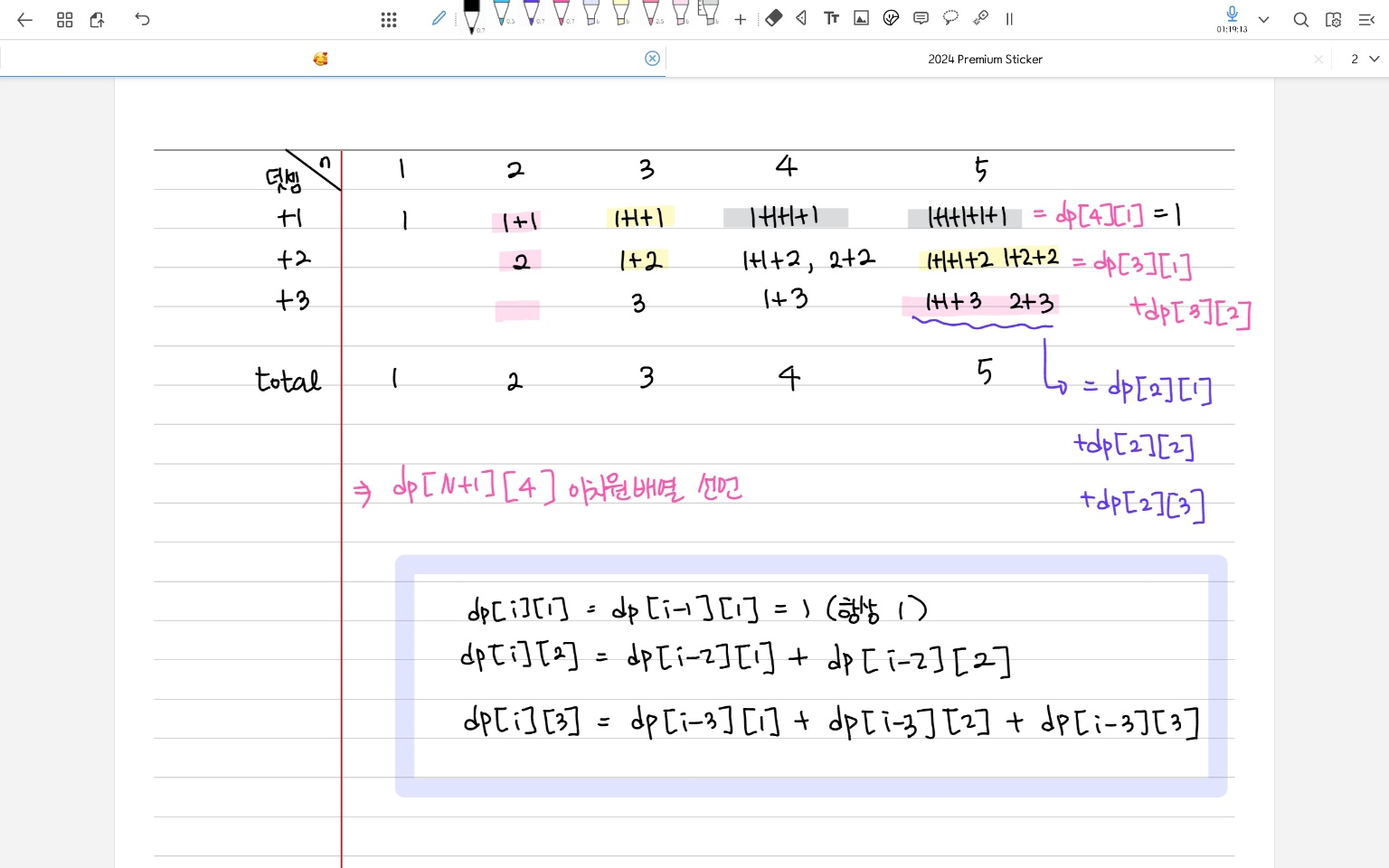

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class OneTwoThreePlusFour {

    public int cntWays(int n) {

        if (n < 4) return n;
       
        int[][] dp = new int[n + 1][4];
        dp[1][1] = 1;
        dp[2][1] = 1;
        dp[2][2] = 1;
        dp[3][1] = 1;
        dp[3][2] = 1;
        dp[3][3] = 1;

        for (int i = 4; i <= n; i++) {
            dp[i][1] = dp[i - 1][1];
            dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
            dp[i][3] = dp[i - 3][1] + dp[i - 3][2] + dp[i - 3][3];
        }
        return dp[n][1] + dp[n][2] + dp[n][3];
    }

    public static void main(String[] args) throws IOException {
        OneTwoThreePlusFour T = new OneTwoThreePlusFour();
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int num = Integer.parseInt(br.readLine());

        for (int i = 0; i < num; i++) {
            int N = Integer.parseInt(br.readLine());
            System.out.println(T.cntWays(N));
        }
    }
}

• 시간초과 안나고 한번에 통과하였다,,,😚😚 확실히 DP를 사용하면 중복 계산을 피해서 연산 횟수를 대폭 감소시킬 수 있는 것 같다!

문제 출처