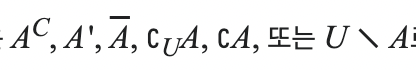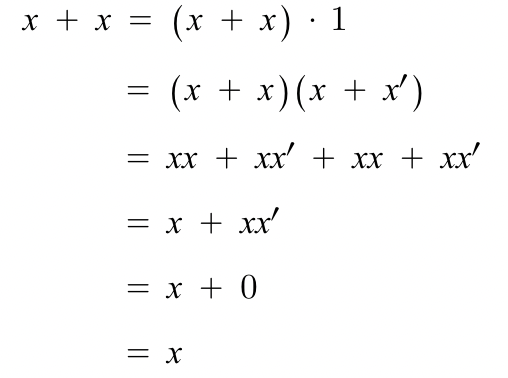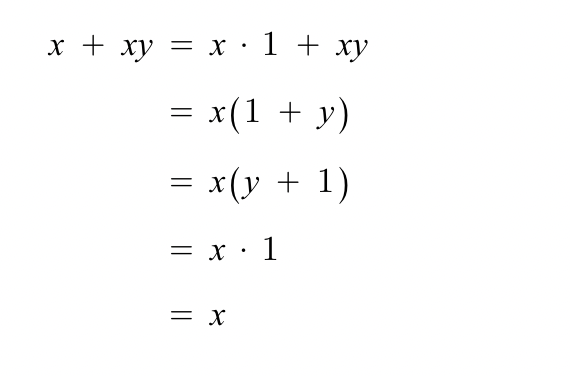집합
: 주어진 성질을 만족시키는 대상들의 모입
집합을 구성하는 원소들로 구성
- 집합 표기 : 알파벳 대문자
- 원소 표기 : 알파벳 소문자
집합을 표현하는 방법
1) 원소나열법(tabular form)
: 원소들을 일일이 나열
S1 = {1,3,5,7,9} S2 = {흰색, 검은색}
- 원소의 개수가 무한 개 이거나 유한 개 혹은 나열 하기 너무 많은 경우 줄임표
...을 사용한다.S1 = {1,2,3, ...,100} : 1부터 100까지 모든 자연수 집합 s2 = {2,4,6,8,10,...} : 모든 양의 짝수의 집합
- 조건 : 집합의 원소들 사이에 눈에 띄는 규칙이 있어야한다.
규칙이 없는 경우 / 모든 실수의 집합을 비롯한 비가산 집합인 경우 표현 불가능
2) 조건제시법(set-builder-form)
: 집합에 속하는 원소들이 만족하여야 하는 조건 제시
S1 = {n|n은 자연수, 1<= n <= 5} : 1부터 5까지의 모든 자연수의 집합
- 규칙 : 중괄호 속 수직선
|이나:을 이용하여 두 구역으로 나눈다.왼쪽 구역 : 집합의 원소를 나타내는 식 오른쪽 구역 : 원소가 만족시킬 조건
3) 오일러 다이어그램(Euler diagram) / 벤 다이어그램(Venn diagram)
: 문자를 쓰는 대신 도형 원을 이용
- 원의 안쪽 : 원이 나타내는 집합에 속하는 부분
- 원의 바깥쪽 : 집합에 속하지 않는 부분
- 겹치는 부분 : 두 집합에 공통으로 속하는 부분
집합의 크기 / 원소 수 표현
|S|: 집합 S내에 있는 서로 다른 원소들의 개수|S1| = 5 |S1| = |S2| : 두 집합의 원소들이 일대일 대응하는 함수가 존재할 때
가산적 집합(countable set)
: 혹은 가산적으로 무한한 집합(countably infinite set) 이라고 하며
일대일 대응 관계에 있는 집합들을 의미한다.Ex) 자연수, 정수, 유리수 알파벳 Σ로 부터 만들어지는 유한한 길이의 문자열(string)들의 집합 : Σ*
집합들 간의 관계
1) 동치 관계 : 집합의 대등, |A| = |B|
2) 반사 관계(추이 관계) : |A| <= |B|
3) 칸토어-반슈타인 정리|A| >= |B| 이고 |A| <= |B| 이면 |A| = |B| 이다.
집합의 연산
1) 합집합(Union) A ∪ B
: 임의의 두 집합 A와 B에 대하여 집합 A 또는 집합 B에 속하는 모든 원소들의 집합
A ∪ B = {x : x ∈ A ∨ x ∈ B} → 원소 x가 A ∪ B에 속할 필요충분조건은 x ∈ A 또는 x ∈ B 이다 라는 의미 cf) ∨ : 또는특징 ↓ n(A ∪ B) = n(A) + n(B) - n(A ∩ B) : 포함/베제의 원리에 따른 두 집합의 원소 개수 관계 A ∪ ∅ = A(항등원) (A ∪ B) ∪ (C ∪ D) = (C ∪ (B ∪ D)) ∪ A : 교환, 결합법칙에 의해 성립됨
+ 포함 / 배제의 원리(inclusion-exclusion principle)
: 유한 집합들에 대하여 합집합의 원소의 개수를 세는 기법 중 하나
a) 집합이 두 개인 경우 : |A ∪ B| = |A| + |B| - |A ∩ B| b) 집합이 세 개인 경우 : |A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |B ∩ C| - |A ∩ C| + |A ∩ B ∩ C| c) 일반적인 경우(집합이 여러개인 경우) : ...
2) 교집합(Intersection) A ∩ B
: 임의의 두 집합 A와 B에 대하여 집합 A 및 집합 B 모두에게 속하는 원소들의 집합
A ∩ B = {x : x ∈ A ∧ x ∈ B} → 원소 x가 A ∩ B에 속할 필요충분조건은 x ∈ A 이고 x ∈ B 이다 라는 의미 cf) ∧ : 이고
- 집합 A와 집합 B가 공통된 원소가 하나도 없는
(A ∩ B = ∅)일 경우 두 집합 A,B를서로소(disjoint)라고 한다.
ex) 유리수, 무리수의 교집합은 공집합임.
3) 차집합(Difference) A - B / A ∖ B
: 임의의 두 집합 A와 B에 대하여 집합 A에서 집합 B의 원소들을 제외한 원소들의 집합
A - B = {x : x ∈ A ∧ x ∉ B} A - B = A - (A ∩ B)
4) 대칭 차집합(Symmetric Difference) A △ B
: 두 집합 A와 B에 대하여 둘 중 한 집합에는 속하지만 둘 모두에는 속하지 않는 원소들의 집합
- 명제의 배타적 논리합과 유사함.
A △ B = {x : x ∈ A ∪ B ∧ x ∉ A ∩ B}
- 교환법칙이 성립됨.
A △ B = B △ A
- 차집합은 대칭 차집합의 부분집합이 된다.
5) 여집합(Complement) Ac
: 전체집합 S가 정의되었을 때 그의 부분집합 집합 A의 여집합은 집합 A에 속하지 않는 원소들의 집합.
표기방법 :Ac = {x ∈ S : x ∉ A} → 임의의 x ∈ S에 대해 x ∈ Ac 일 필요충분조건은 x ∉ A이다.
6) 집합 B의 부분집합(Subset) A : A ⊆ B
: 두 집합 A와 B에 대하여 집합 B의 부분집합 A는 모든 원소가 B에도 속하는 집합
A ⊆ B = {∀ x ∈ A : x ∈ B}
- A = B 인 경우에도 A는 B의 부분집합
- B가 A의 초집합 또는 상위집합(superset)
진부분집합(Proper subset)
: A가 B의 부분집합이고, A에 속하지 않는 B의 원소가 적어도 하나 존재하는 경우
즉, 자신과 똑같은 집합을 제외한 진짜 부분집합A ⊂ B
- B가 A의 진초집합 또는 진상위집합(superset)
7) 멱집합(Power set) 2^S
: 집합의 모든 부분집합을 모아 놓은 것.
- 집합 S에 대한 멱집합 P(S)는 S의 모든 부분집합의 집합이다.
P(S) = {A : A ⊆ S}
- 공집합과 원래 집합을 원소로 포함한다.
- 유한 집합 S의 멱집합은 유한 집합이며 크기는
|P(S)| = 2^|S|임.
무한 집합의 멱집합은 비가산 집합 크기는|P(S)| = 2^|S|임.
2^|S|: 기수의 거듭 제곱, 집합의 크기이다.
❗️ 어떤 집합의 원소의 개수가 n이라면 멱집합의 개수는2^n이다.
8) 곱집합(Cartesian product) A X B
: 데카르트 곱이라고도 불리며 각 집합의 원소를 각 성분으로 하는 순서쌍(Ordered pair)들의 집합
- 하나의 순서쌍은 순서로 구분되는 원소들의 쌍으로
(a,b)로 표현- 순서쌍의 원소들의 순서에 의해 구분됨으로
(a,b) != (b,a)이다.A X B = {(a, b) : a ∈ A ∧ a ∈ B}
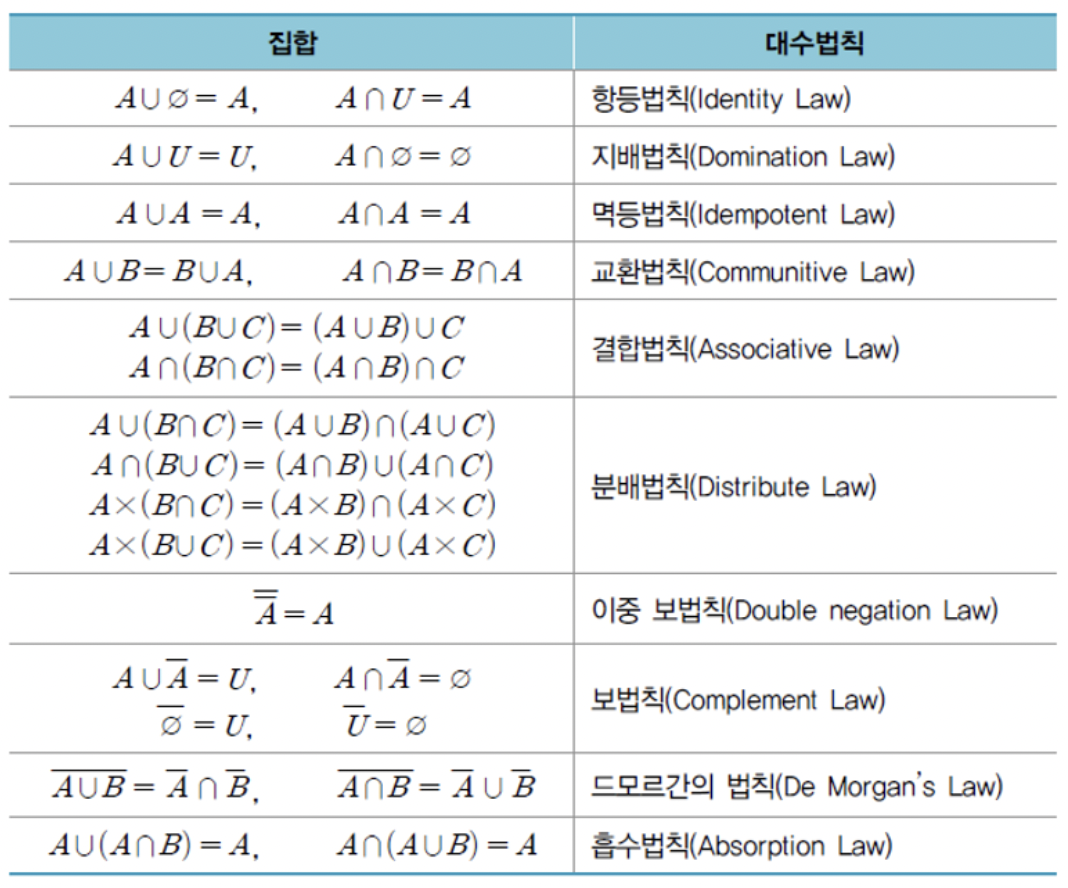
9) 집합의 대수법칙
- 결합법칙 : 같은 연산들이 나열된 경우 사용 가능.
- 분배법칙 : 다른 연산들이 섞어있을 때 사용
- 보법칙 : 역의 역
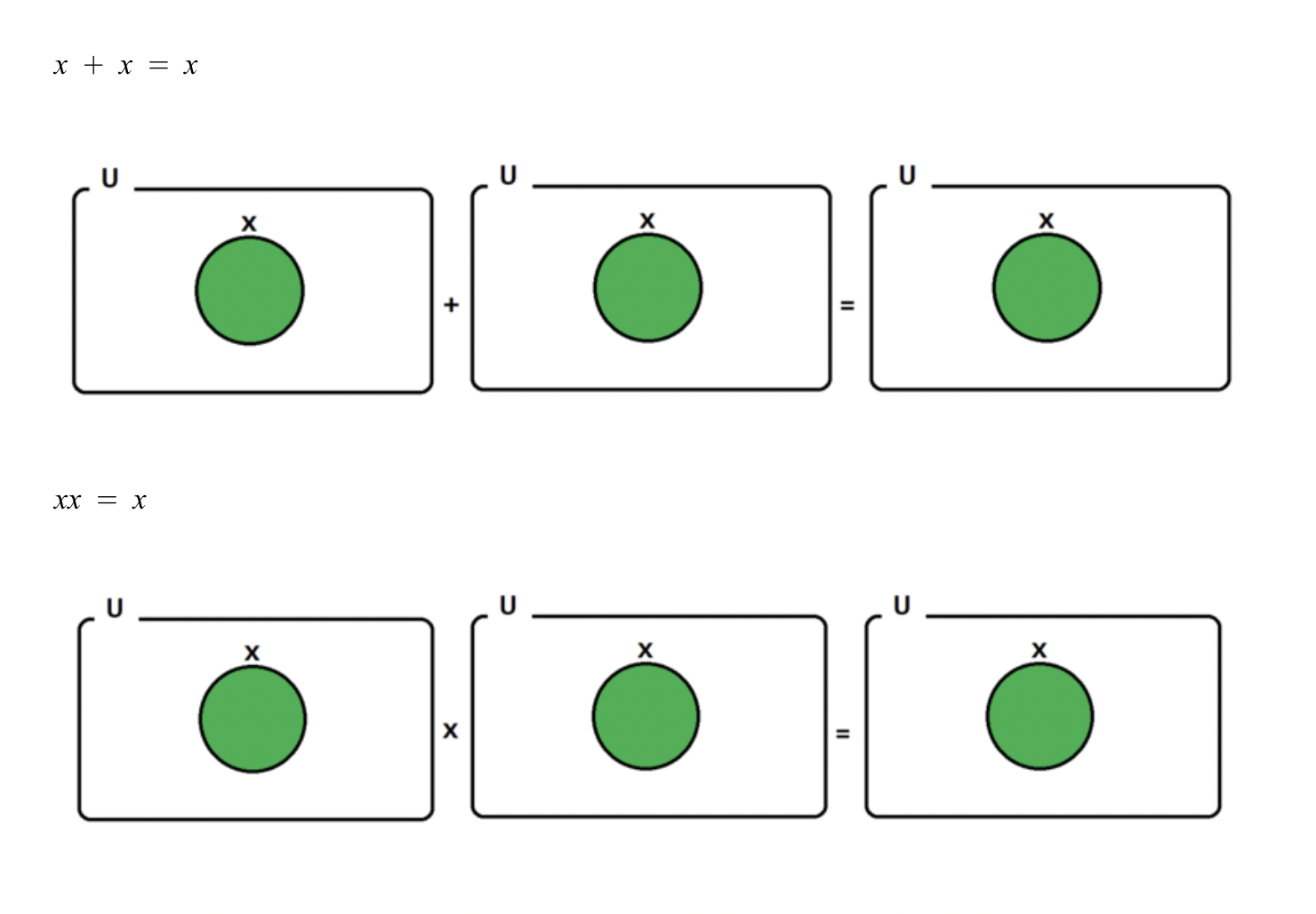
멱등법칙 벤다이어그램 / 증명
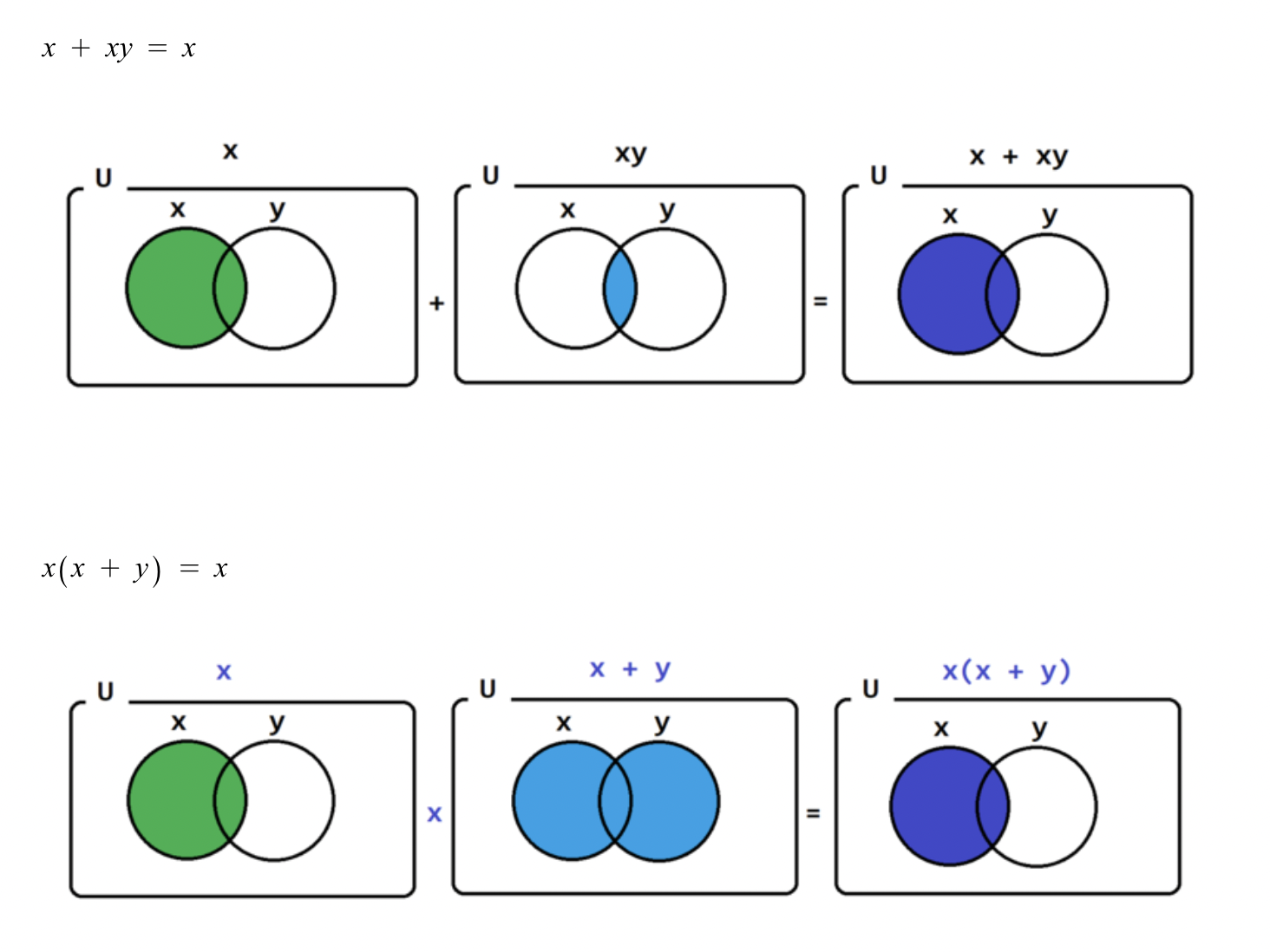
흡수법칙 벤다이어그램 / 증명
출처) https://m.blog.naver.com/zlatmgpdjtiq/221688799155