[PS] 파이썬 QUEUE 구현체별 시간 복잡도 비교

⚠️ 공부 과정에서 배운 내용과 개인 생각을 기록했습니다.
내용 정정 및 논의가 더 필요한 내용은 편하게 댓글 달아주세요!

💥 Queue

• 먼저 삽입된 데이터가 먼저 삭제되는 FIFO 기반의 데이터 처리에 적합한 자료구조
• 현실에서는 운영체제 프로세스 스케쥴링, 네트워크 패킷 처리 등 작업 순서에 맞게 처리 되어야 하는 등의 상황에서 주로 사용

기본적인 메서드로 다음 2가지를 가진다.

• enqueue(맨 마지막에 원소 삽입)
• dequeue(맨 처음 원소 삭제 및 반환)

💥 Python에서 제공하는 Queue

직접 구현할 수도 있지만,
파이썬에서 미리 구현된 큐를 활용할 수도 있다.
코테 풀이에 주로 등장하는 것들 위주로 뽑아보자면 아래 3가지 정도가 있는듯 하다

1) list
2) queue.Queue
3) collections.deque

💥 Operation별 시간 복잡도 비교

1) Enqueue(맨 마지막에 원소 삽입)

• list - append()
• collections.deque - append()
• queue.Queue - put()

위의 3가지 연산 모두 O(1)의 시간 복잡도를 가진다.

2) Dequeue(맨 처음 원소 삭제 및 반환)

• list - pop(0)
  맨 앞의 원소를 제거한뒤, 모든 원소에 대해 왼쪽으로 shift 연산이 필요하므로 O(n)

• collections.deque - popleft()
  collections.deque는 이중 연결 리스트 기반으로 구현되어 있으므로,
  양방향 원소에 대한 삽입/삭제 연산이 O(1)로 가능하다
  

• queue.Queue - get()

  queue.Queue의 경우, 내부적으로 deque를 사용하고 있으므로 위와 동일

  참고로 아래는 queue.Queue의 라이브러리 내부 코드이다. (python 3.11)

   # queue.py 
   # python 3.11
  
   class Queue:
  
      ...
  
      # Initialize the queue representation
      def _init(self, maxsize):
          self.queue = deque()
  
      def _qsize(self):
          return len(self.queue)
  
      # Put a new item in the queue
      def _put(self, item):
          self.queue.append(item)
  
      # Get an item from the queue
      def _get(self):
          return self.queue.popleft()

  queue.Queue는 Locking 연산이 추가되므로
  멀티 스레딩의 활용 등 실무에서는 유용하지만, 코테용으로는 deque 자체를 쓰는게 더 적합하다고 판단된다.

More about 1

우선순위 큐

• 삽입 순서가 아니라, 우선순위에 따라 데이터를 처리하는 큐

아래 프로그래머스 문제를 풀이하다가, 정리하게 되었다.
(프로세스: https://school.programmers.co.kr/learn/courses/30/lessons/42587)

최대값을 구하는 연산이 계속 필요한 문제이다.
우선순위 큐 관련 문제에서 max() 연산 + 리스트에 대한 pop()을 활용한 풀이를 볼 수 있었다.

하지만,
단순히 최대값을 한두번 조회하고 끝나는 것이 아니라,
최대값을 계속 꺼내오며 배열 자체에 수정이 필요하다면
priorityQueue 사용을 고려해보면 좋을 것 같다.

min(), max() → 최악의 경우 모든 원소를 순회해야 하므로 O(n)
리스트에 대한 pop() → O(n)(맨 뒤 요소 제거일 경우, O(1))

min-heap, max-heap 기반 pop() → O(logN)
(** 단순히 최대/최소값 조회만 필요하면, O(1)로 연산 가능)

파이썬에서는 아래와 같은 우선순위 큐를 제공한다

• queue 라이브러리의 PriorityQueue
• heapq 모듈

🚥 코테에서는 멀티 스레딩까지 고려할 필요 없으므로,
스레드 safe하지는 않지만 더 빠른 heapq 사용이 더 적합하다고 생각된다

🚥 보통 우선 순위 큐를 생성은 O(nlogn)를 가진다.

import heapq

x = []
for value in [3, 1, 4, 1, 5, 9, 2]:
    heapq.heappush(x, value)

다만, 특정 리스트를 한번에 우선순위 큐로 바꾸고자 한다면, heapq.heapify()를 통해 O(n)으로 해결이 가능하다.
이는 입력된 리스트 자체를 수정한다.

import heapq

x = [3, 1, 4, 1, 5, 9, 2]
heapq.heapify(x)

# heapq.py
# python 3.11

def heapify(x):
    """Transform list into a heap, in-place, in O(len(x)) time."""
    n = len(x)
    # Transform bottom-up.  The largest index there's any point to looking at
    # is the largest with a child index in-range, so must have 2*i + 1 < n,
    # or i < (n-1)/2.  If n is even = 2*j, this is (2*j-1)/2 = j-1/2 so
    # j-1 is the largest, which is n//2 - 1.  If n is odd = 2*j+1, this is
    # (2*j+1-1)/2 = j so j-1 is the largest, and that's again n//2-1.
    for i in reversed(range(n//2)):
        _siftup(x, i)

** heapq는 min-heap을 기반이므로, max-heap이 필요한 경우 원소들을 음수값으로 바꾼 뒤 삽입해야 한다.

참고로,

가장 우선순위에 해당하는 맨 앞 요소(root node)를 pop 연산은 아래와 같은 세부 과정이 진행된다.

1. 맨 앞 요소(root node)와 맨 마지막 원소(leaf node)를 바꿈: O(1)
2. leaf node를 pop(): O(1)
3. 우선순위가 가장 높은 원소가 다시 root node에 갈 수 있도록, 트리를 재정렬 하는 과정이 필요 : 트리의 높이만큼 시간 소요 O(logN)

크게 위의 3과정으로 진행되기 때문에, heap 기반 우선 순위 큐의 pop연산은 O(logN)의 시간복잡도를 가진다.
이는 heap기반 우선 순위 큐의 경우, root node에 대한 우선순위 정렬은 보장되지만 자식 노드들 간의 정렬은 보장되지 않기에 pop()연산에서도 heapify의 과정이 필요하기 때문이다.

More about 2

실무에서 알고 있으면 좋을 개념들

• queue.Queue: 멀티 스레딩 환경에서의 통신에 적합
• multiprocessing.Queue: 멀티 프로세싱 환경에서의 통신에 적합
• asyncio.Queue: 비동기 프로그래밍에서 코루틴간의 통신에 적합

Summary

🍔 단일 스레드라면, 굳이 queue 라이브러리의 Queue를 사용할 필요 없이 collections.deque를 활용
🥨 min(), max() 연산이 자주 사용된다면, 우선 순위 큐를 고려

🤖 아래는 오늘 언급한 파이썬의 queue 구현체별 시간 복잡도 비교
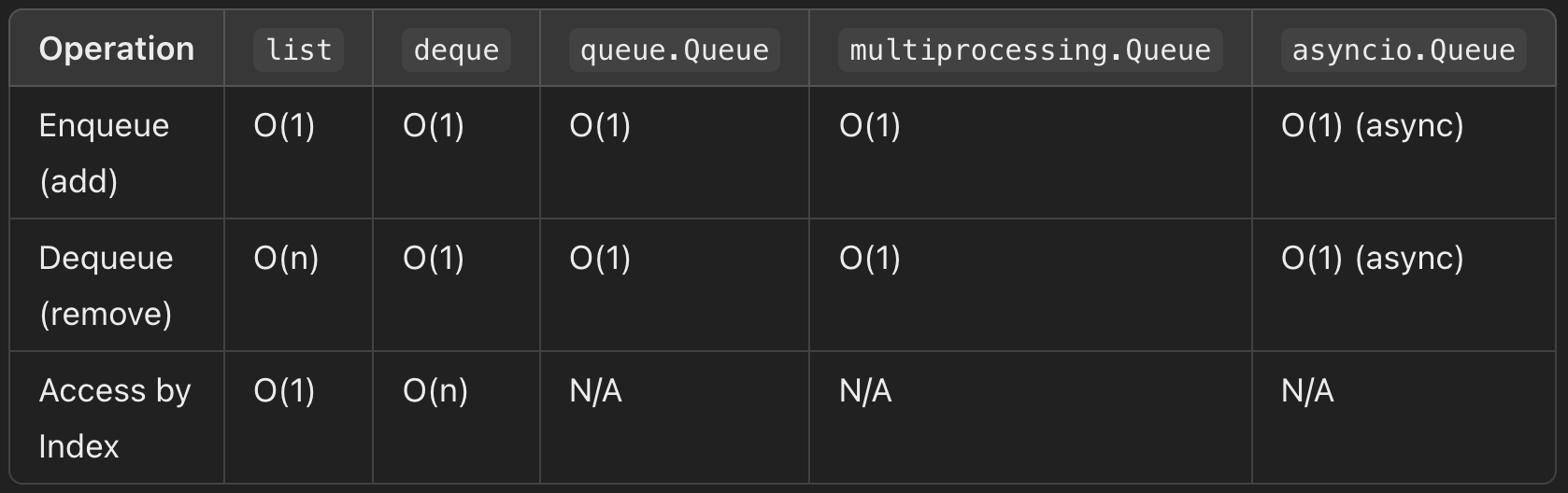[테이블 출처: Chat GPT]