백준 11660 - 구간 합 구하기 5

문제

N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.

예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.

1	2	3	4
2	3	4	5
3	4	5	6
4	5	6	7

여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.

표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.

입력

첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)

출력

총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.

문제풀이

질의의 개수가 100000 이고 알고리즘 분류에서도 다이나믹 프로그래밍, 누적 합이 적혀 있기 때문에 2차원 배열의 구간 합을 이용하여 풀어야 함을 알 수 있다.

2차원 배열의 구간 합을 정의하면 다음과 같다.

D[X][Y] = (0,0) 부터 (X,Y) 까지의 사각형 영역 안에 있는 수들의 합

그림으로 예시를 들어보면
D[2][3] = (0,0) 부터 (2, 3) 까자의 사각형 영역 안에 있는 수들의 합
즉, 1 + 2 + 3 + 2 + 3 + 4 = 15이다.
이런 식으로 D 이차원 합 배열의 값을 채워주면 오른쪽과 같은 결과가 나온다.

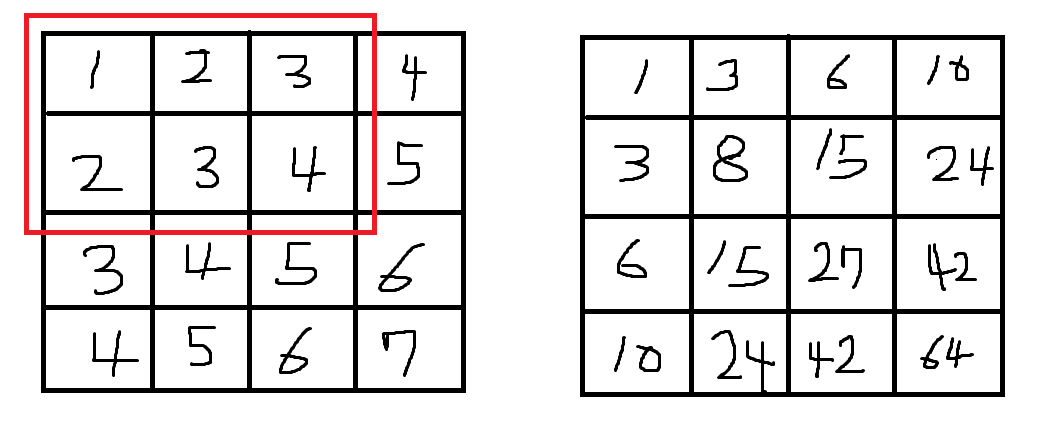
이를 식으로 도출해보면

D[i][j] = D[i][j - 1] + D[i - 1][j] + A[i][j] - D[i - 1][j - 1]

* D[i - 1][j - 1] 을 빼주는 이유는 중복으로 더해진 구간 합을 없애기 위함이다.

그리고 이제 (2,2) 에서 (3,4)까지의 구간 합을 구한다면 아래 그림과 같은 결과가 나온다.

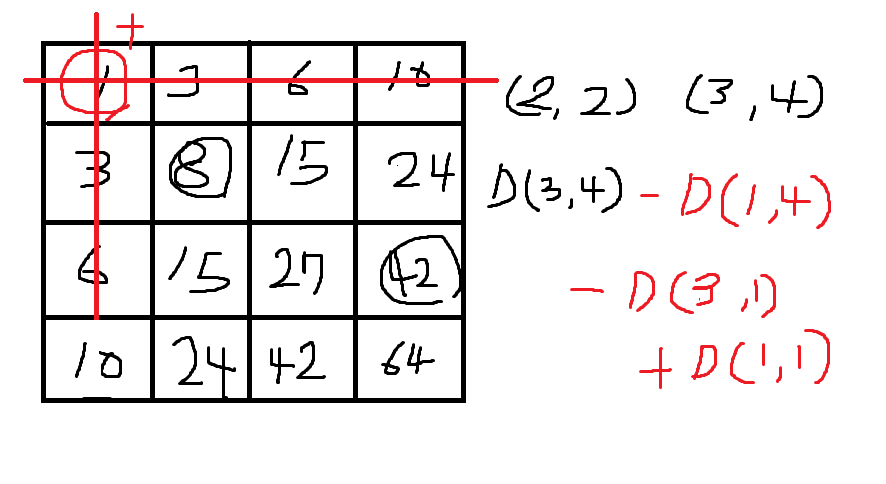
이를 또 식으로 도출해보면

(X1, Y1), (X2, Y2) 가 주어진다면

D[X2][Y2] - D[X1 - 1][Y2] - D[X2][Y1 - 1] + D[X1 - 1][Y1 - 1]

이제 풀이 과정을 코드의 적용해보자

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

class 구간합구하기5 {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken(" "));
        int M = Integer.parseInt(st.nextToken(" "));

        int A[][] = new int[N + 1][N + 1];
        int D[][] = new int[N + 1][N + 1];

        for(int i = 1; i <= N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j = 1; j <= N; j++){
                A[i][j] = Integer.parseInt(st.nextToken(" "));
            }
        }

        for(int i = 1; i <= N; i++){
            for(int j = 1; j <= N; j++){
                D[i][j] = D[i - 1][j] + D[i][j - 1] + A[i][j] - D[i - 1][j - 1];
            }
        }

        StringBuilder sb = new StringBuilder();

        for(int i = 0; i < M; i++){
            st = new StringTokenizer(br.readLine());
            int X1 = Integer.parseInt(st.nextToken(" "));
            int Y1 = Integer.parseInt(st.nextToken(" "));
            int X2 = Integer.parseInt(st.nextToken(" "));
            int Y2 = Integer.parseInt(st.nextToken(" "));

            int result = D[X2][Y2] - D[X1 - 1][Y2] - D[X2][Y1 - 1] + D[X1 - 1][Y1 - 1];
            sb.append(result + "\n");
        }

        System.out.println(sb);

    }

}

문제를 풀고나서

풀었던 문제라서 쉽게 도출이 되었었지만 구간 합에 대한 이해가 아직 많이 부족한 것 같다. 좀 더 여러 문제를 풀어보면서 익숙해지고자 끊임 없이 풀어야겠다.