백준 1167 - 트리의 지름

문제

트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.

입력

트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.

먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

예제 입력 1

5
1 3 2 -1
2 4 4 -1
3 1 2 4 3 -1
4 2 4 3 3 5 6 -1
5 4 6 -1

예제 출력 1

11

문제 풀이

이 문제는 핵심 아이디어가 필요한 문제라고 한다.

가장 긴 경로 찾기 아이디어 :
임의의 노드에서 가장 긴 경로로 연결되어 있는 노드는 트리의 지름에 해당하는 두 노드 중 하나이다.

처음 아이디어를 봤을 때는 감이 오지 않았다....
그래서 검색을 하다가 좋은 블로그가 있어서 참고하였다.

https://moonsbeen.tistory.com/101

결국 트리의 지름을 구하기 위해서는 임의의 정점 $x$ 를 하나 잡고 그 정점에서 가장 먼 정점인 $y$ 를 찾는다.

그 후 $y$에서 가장 먼 정점인 $z$를 찾으면 되는 것이다.

여기서는 BFS를 이용하여 문제를 푸는 것이 좋을것 같다.

필요한 것들은 BFS 를 풀 때 필요한 인접리스트 A 와 방문 배열을 저장하는 visited 그리고 거리를 저장할 배열 distance 가 있다.

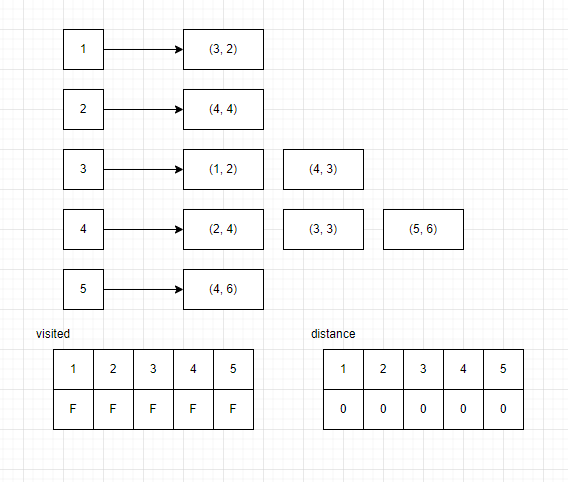여기서 노드는 (3, 2) 형태로 이루어졌기 때문에 클래스 형태로 표현해야 한다.

1. 임의의 노드를 1부터 잡고 시작하면 방문배열에는 1을 true 로 바꿔주고 (3, 2) 가 뜻하는 바는 노드 3까지의 거리가 2만큼 떨어졌다는 것이다. 따라서 distance[3]에 떨어진 거리 2를 더해준다.
   

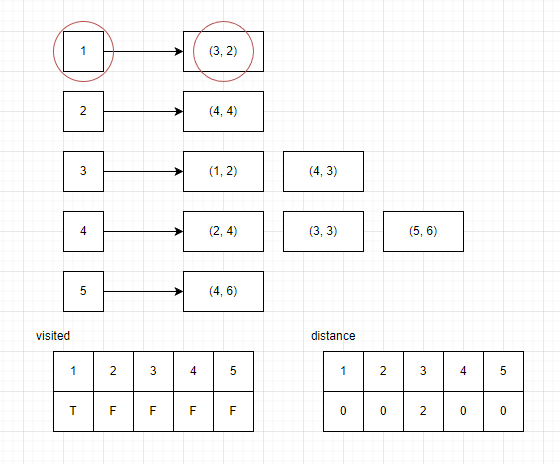
2. 3 노드에서 연결되어 있는 노드는 (1, 2) ,(4, 3) 가 있지만 1은 이미 방문하 상태이기 때문에 (4, 3)으로 이동한다. 방문배열에는 4를 true로 바꿔주고 현재 떨어진 거리(2) 에서 3을 더해준 5를 distance[4]에 더해준다.
   

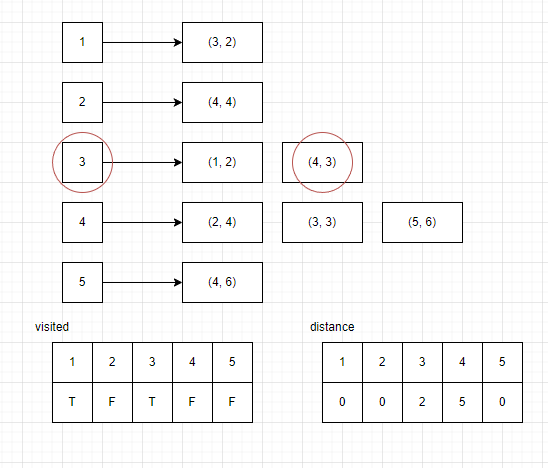
3. 4 노드에서 연결되어 있는 노드는 (2, 4), (5, 6) 이다 (3, 3)은 이미 방문한 곳이기 때문에 제외한다.
   (2, 4) 로 이동하면 방문배열에는 2를 true로 바꿔주고 distance[2] 에는 현재 떨어진 거리(5) 에서 4를 더해준다.
   (5, 6) 로 이동하면 방문배열에는 5를 true로 바꿔주고 distance[5] 에는 현재 떨어진 거리 (5)에서 6을 더해준다.

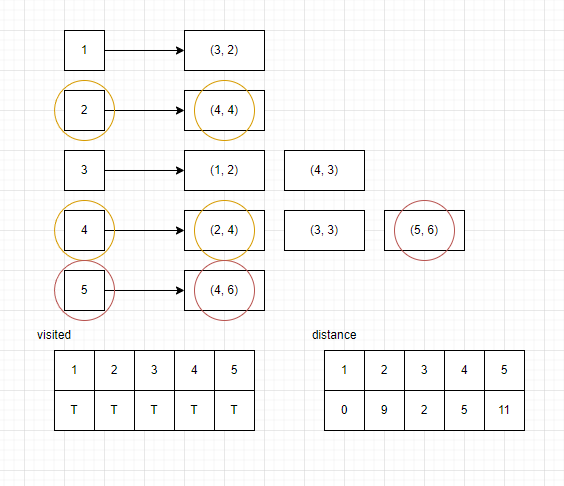
4. 이제 모든 노드를 방문하였기 때문에 distance에서 가장 높은 값을 가진 11 의 인덱스인 5를 이용하여 위와 같이 BFS를 한번 더 실행하면 트리의 지름을 구할 수가 있다.

이를 코드에 적용하면 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class 트리의지름 {

    static ArrayList<Edge>[] A;
    static boolean[] visited;
    static int[] distance;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        A = new ArrayList[N + 1];
        visited = new boolean[N + 1];
        distance = new int[N + 1];

        for(int i = 1; i <= N; i++) {
            A[i] = new ArrayList<>();
        }

        StringTokenizer st;
        for(int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            while(true) {
                int end = Integer.parseInt(st.nextToken());
                if(end == -1)
                    break;
                int length = Integer.parseInt(st.nextToken());
                A[start].add(new Edge(end, length));
            }
        }

        BFS(1);
        int Max = 1;
        for(int i = 2; i < distance.length; i++) {
            if(distance[Max] < distance[i]) {
                Max = i;
            }
        }

        visited = new boolean[N + 1];
        distance = new int[N + 1];
        BFS(Max);
        Arrays.sort(distance);
        System.out.println(distance[N]);

    }

    private static void BFS(int index) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(index);
        visited[index] = true;

        while(!queue.isEmpty()) {
            int now_node = queue.poll();
            for(Edge e : A[now_node]) {
                int end = e.end;
                int length = e.length;
                if(!visited[end]) {
                    visited[end] = true;
                    queue.add(end);
                    distance[end] = distance[now_node] + length;
                }
            }
        }
    }

    static class Edge {
        int end;
        int length;

        public Edge(int end, int length){
            this.end = end;
            this.length = length;
        }

    }

}

회고

트리의 지름을 구하는 방법을 이해하기가 힘들었다. 사실 아직까지도 누군가 증명하라고 하면 버버벅 거릴 것 같다. 이 증명만 안다면 문제를 푸는데는 크게 어려울 것은 없어 보이는데 틈틈히 계속 트리의 지름을 보면서 공부하도록 하겠다.