백준 2178 - 미로 탐색

YongHyun·2023년 4월 24일

백준, 프로그래머스 - 코딩테스트

목록 보기

27/43

문제

시간 제한 1초
N×M크기의 배열로 표현되는 미로가 있다.

1	0	1	1	1	1

1	0	1	0	1	0

1	0	1	0	1	1

1	1	1	0	1	1

미로에서 1은 이동할 수 있는 칸을 나타내고, 0은 이동할 수 없는 칸을 나타낸다. 이러한 미로가 주어졌을 때, (1, 1)에서 출발하여 (N, M)의 위치로 이동할 때 지나야 하는 최소의 칸 수를 구하는 프로그램을 작성하시오. 한 칸에서 다른 칸으로 이동할 때, 서로 인접한 칸으로만 이동할 수 있다.

위의 예에서는 15칸을 지나야 (N, M)의 위치로 이동할 수 있다. 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.

입력

첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.

출력

첫째 줄에 지나야 하는 최소의 칸 수를 출력한다. 항상 도착위치로 이동할 수 있는 경우만 입력으로 주어진다.

예제 입력 1

4 6
101111
101010
101011
111011

예제 출력 1

15

문제 풀이

N과 M의 최댓값은 100으로 매우 작기 때문에 시간 제한에 크게 신경 쓸 필요는 없어 보인다. 지나가야 하는 최소의 칸 수를 구하면 되는 문제인데 이 때 사용할 알고리즘이 DFS 와 BFS 로 추려낼 수 있다. 왜냐하면 완전탐색을 진행하면서 몇 번째 깊이에 값을 찾을 수 있는 것과 동일하기 때문이다.

그렇다면 DFS와 BFS 중 어떤 것을 선택해야 하는가?
둘 중 어떤것을 선택하여도 문제를 푸는데는 상관이 없지만 BFS를 사용하는 것이 해당 깊이에서 갈 수 있는 노드 탐색을 마치고 다음 깊이로 넘어가기 때문에 BFS 를 선호한다고 한다.

N = 4, M = 6
101111
101010
101011
111011
형태로 입력됬다고 가정하면 다음과 같이 그림으로 표현할 수 있다.

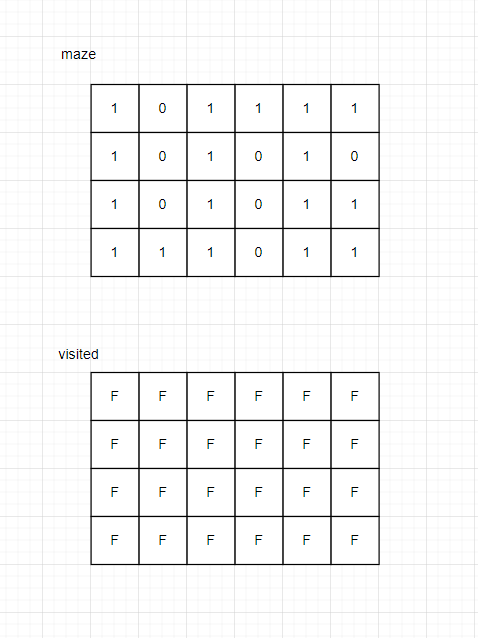
그 후 BFS 알고리즘을 수행한다. 처음 maze[0][0] 부터 시작하는데 칸을 셀 때에는 시작 위치와 도착 위치도 포함한다.는 지문이 있기 때문에 방문 배열에 visited[0][0] 을 true로 바꿔준다. 그리고 위, 아래, 오른쪽, 왼쪽 으로 이동할 수 있는지 판단한다. 현재는 오른쪽, 아래 로 이동이 가능하지만 여기서 또 판단해줘야 하는 것이 0은 이동할 수 없는 칸이기 때문에 아래로만 이동이 가능하다는 것을 최종적으로 알 수 있다.

아래로 이동할 칸은 현재 값에서 1을 더한 값으로 변경시켜준다. 이렇게 하면 깊이가 계속 내려가는 것이 이동한 거리와 같다는 것을 알게 된다.

위의 과정을 한 번 더 거치면 아래로 내려갈 수 밖에 없기 때문에 현재 값에서 1을 더한 값인 3으로 변경 시켜준다.

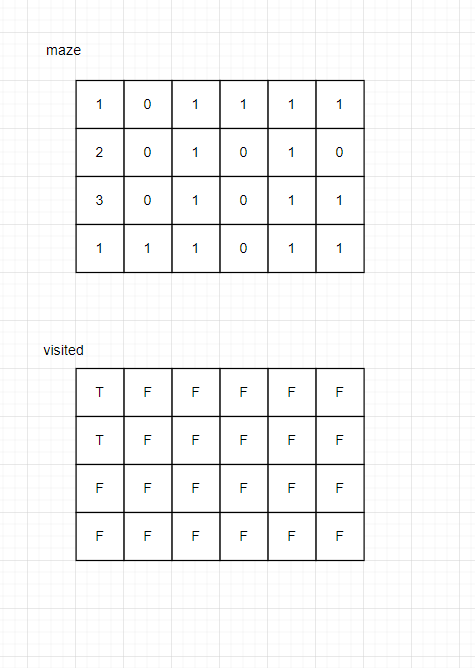
이렇게 BFS 알고리즘을 계속 수행하다보면 다음과 같은 결과가 나온다.

이를 코드에 적용시키면 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class 미로탐색 {

    static int[] dx = {0, 1, 0, -1};    // 위, 오른쪽, 왼쪽, 아래 방향으로 움직이기 위한 방향표
    static int[] dy = {1, 0, -1, 0};
    static int[][] maze;                // N * M 크기의 배열 미로
    static boolean[][] visited;             // 방문했던 곳을 체크하기 위한 배열
    static int N, M;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        maze = new int[N][M];       // 미로 N * M 크기로 초기화
        visited = new boolean[N][M];    // 방문 배열 N * M 크기로 초기화


        /*
            maze 의 값을 채워주는 로직
         */
        for(int i = 0; i < N; i++) {
            String[] line = br.readLine().split("");
            for(int j = 0; j < M; j++) {
                maze[i][j] = Integer.parseInt(line[j]);
            }
        }

        BFS(0, 0);
        System.out.println(maze[N - 1][M - 1]);

    }

    private static void BFS(int i, int j) {
        Queue<int[]> queue = new LinkedList<>();	// BFS 알고리즘을 사용하기 위해서는 Queue 를 사용하여야 한다.
        queue.offer(new int[] {i,j});				// queue의 현재 위치의 노드 값을 넣어준다.
        visited[i][j] = true;						// 방문배열에도 체크해준다.

        while(!queue.isEmpty()) {					
            int[] now = queue.poll();			
            for(int k = 0; k < 4; k++) {
                int x = now[0] + dx[k];				// 현재위치의 노드 값이 어디로 이동할 수 있는지 파악한다.
                int y = now[1] + dy[k];
                if(x >= 0 && y >= 0 && x < N && y < M) {	// 범위를 벗어나는지 체크
                    if(!visited[x][y] && maze[x][y] != 0) { // 방문했던 곳인지 && 0이어서 이동할 수 없는지 체크
                        visited[x][y] = true;		
                        maze[x][y] = maze[now[0]][now[1]] + 1; // 현재 위치한 곳에서 + 1 한 값 즉, 깊이를 다음 이동할 곳에 값으로 변경시켜준다.
                        queue.add(new int[] {x, y});
                    }
                }
            }
        }
    }
}