백준 1929 - 소수 구하기

YongHyun·2023년 5월 18일

Java 백준 코딩테스트

백준, 프로그래머스 - 코딩테스트

목록 보기

36/43

문제

시간 제한 2초

M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.

출력

한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.

예제 입력 1

3 16

예제 출력 1

3
5
7
11
13

문제 풀이

M 이상 N 이하의 소수를 출력하는 문제이다. 먼저 소수란 자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수를 뜻하기도 하며 같은 의미로 1과 자기 자신 외에 약수가 존재하지 않는 수라고도 뜻할 수 있다.

이렇게 소수를 구하는데 이중 for 문을 이용하여 접근하는 것도 있지만 유명한 에라토스테네스의 체 원리를 알아두면 유용하다. 아니 소수를 구하는 이런 문제에서는 꼭 기억해야 하는 거라고 생각한다.

에라토스테네스의 체 원리

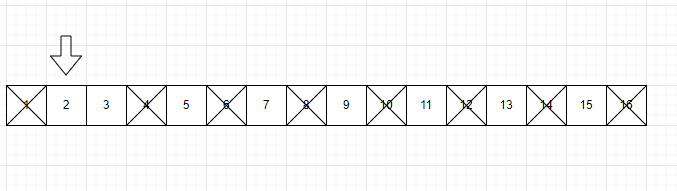
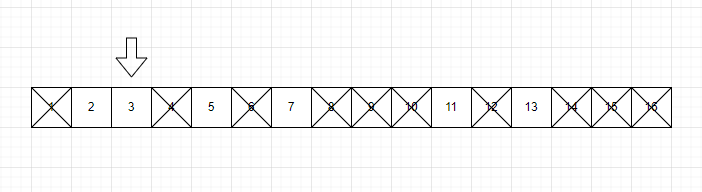
구하고자 하는 소수의 범위만큼 1차원 배열을 생성합니다. (예제 입력 1처럼 1 부터 16까지로 입력받았다고 가정)

2부터 시작하고 현재 숫자가 지워지지 않을 때는 현재 선택된 숫자의 배수에 해당하는 수를 배열에서 끝까지 탐색하면서 지웁니다. 이때 처음으로 선택된 숫자는 지우지 않습니다.

배열의 끝까지 2를 반복한 후 배열에서 남아 있는 모든 수를 출력합니다.
[2, 3, 5, 7, 11, 13] 총 6개가 정답이다.

이를 코드에 적용하면 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 소수구하기 {

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int M = Integer.parseInt(st.nextToken());
        int N = Integer.parseInt(st.nextToken());
        boolean[] prime = new boolean[N + 1];	// N + 1 만큼에 소수를 체크할 배열 prime

        prime[1] = true; // 1은 소수가 아니기 때문에 제외
        for (int i = 2; i <= Math.sqrt(N); i++) {	// N의 제곱근 까지 탐색

            if(prime[i] == true) {
                continue;
            }

            for(int j = i + i; j <= N; j += i) {
                prime[j] = true;
            }

        }

        StringBuilder sb = new StringBuilder();
        for (int i = M; i <= N; i++) {
            if (!prime[i]) {
                sb.append(i).append("\n");
            }
        }

        System.out.println(sb);
    }
}

에라토스테네스의 체 시간복잡도 및 분석

참고 블로그 : https://st-lab.tistory.com/81

소수를 구하는 문제에서 이중 for 문을 이용하면 시간복잡도는 $O(N^2)$ 이 나온다고 할 수 있지만 실제 시간 복잡도는 일반적으로 $O(Nlog(logN))$ 입니다. 이유는 배수를 삭제하는 연산으로 실제 구현에서 바깥쪽 for 문을 생략하는 경우가 빈번하게 발생하기 때문이다.

N의 제곱근까지만 탐색하는 이유는 N이 a*b 라고 가정했을 때, a 와 b 모두 N의 제곱근보다 클 수는 없다고 한다. 예시로 N 이 16인 경우를 생각해보자
1 X 16
2 X 8
4 X 4
8 X 2
16 X 1

a와 b 중 하나는 반드시 $\sqrt{N}$ 보다 작거나 같다. 즉 $\sqrt{N}$ 이하의 자연수 중에 나누어 떨어지는 수가 있다면 이는 1과 N 을 제외한 다른 자연수가 N의 약수라는 의미이므로 소수가 아니게 된다.
16보다 작은 숫자는 항상 4보다 작은 약수를 갖게 된다고 결론을 내릴 수 있다. 따라서 4 까지만 확인하고 소수 판별을 진행하면 된다.