
문제 설명
첫 번째 분수의 분자와 분모를 뜻하는 numer1, denom1, 두 번째 분수의 분자와 분모를 뜻하는 numer2, denom2가 매개변수로 주어집니다. 두 분수를 더한 값을 기약 분수로 나타냈을 때 분자와 분모를 순서대로 담은 배열을 return 하도록 solution 함수를 완성해보세요.
제한 사항
0 <numer1, denom1, numer2, denom2 < 1,000
입출력 예
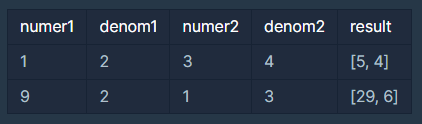
풀이 과정
처음 풀이를 할때는 일반 분수의 합으로 계산하면 된다고 생각하여서 다음과 같이 생각했지만
풀이 : numer1 * denum2 + numer2 * denum1/denom1 * denom2
결과 : 10 / 8약분해야 하는 과정에서 최대공약수를 구해야 하기 때문에
이 최대공약수를 구하는 방법을 찾다 보니 유클리드 호제법이라는 알고리즘을 알게 되었다.
유클리드 호제법 또는 유클리드 알고리즘은 2개의 자연수 또는 정식의 최대공약수를 구하는 알고리즘의 하나이다.
1071과 1029의 최대공약수를 구하면,
1071은 1029로 나누어 떨어지지 않기 때문에, 1071을 1029로 나눈 나머지를 구한다. ≫ 42
1029는 42로 나누어 떨어지지 않기 때문에, 1029를 42로 나눈 나머지를 구한다. ≫ 21
42는 21로 나누어 떨어진다.
따라서, 최대공약수는 21이다.
출처:https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
위의 예시를 따르면 10과 8의 최대공약수는
10/8 => 2
8/2 => 0
이때 나머지가 0이 되었을 때 나누는 수가 최대공약수이다.
따라서 2가 최대 공약수이고 분모와 분자의 각 각 2로 나눠주면
5/4 가 나와 정답인 것을 알게 되었다.
정답
class Solution {
public int eucd(int bn, int sn) {
int r = bn % sn;
if (r == 0) {
return sn;
} else {
return eucd(sn, r);
}
}
public int[] solution(int numer1, int denom1, int numer2, int denom2) {
int numerator = numer1 * denom2 + numer2 * denom1;
int denominator = denom1 * denom2;
int gcd = eucd(numerator, denominator);
int[] answer = {numerator/gcd, denominator/gcd};
return answer;
}
}후기
여러 곳의 검색을 통해서 푼 문제라 기본기가 많이 부족한 것 + 알고리즘에 익숙해질 때까지
여러 문제를 풀어봐야 겠다는 생각을 가지게 되었다.
