📘 다익스트라(Dijkstra) 알고리즘

📖 개요

📌 음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘.

• 에츠허르 다익스트라가 고안해낸 알고리즘으로 지금까지 계속 개선되어오고 있다.

• 다이나믹 프로그래밍 활용한 대표적인 최단 경로 탐색 알고리즘이다.

• GPS 소프트웨어 등에 사용된다.

📖 알고리즘의 설명

가능한 적은 비용으로 가장 빠르게 해답에 도달하는 경로를 찾아내는 대부분의 문제에 응용되며

통상적으로 임의의 노드에서 다음 노드로 가는 값을 비용이라고 한다.

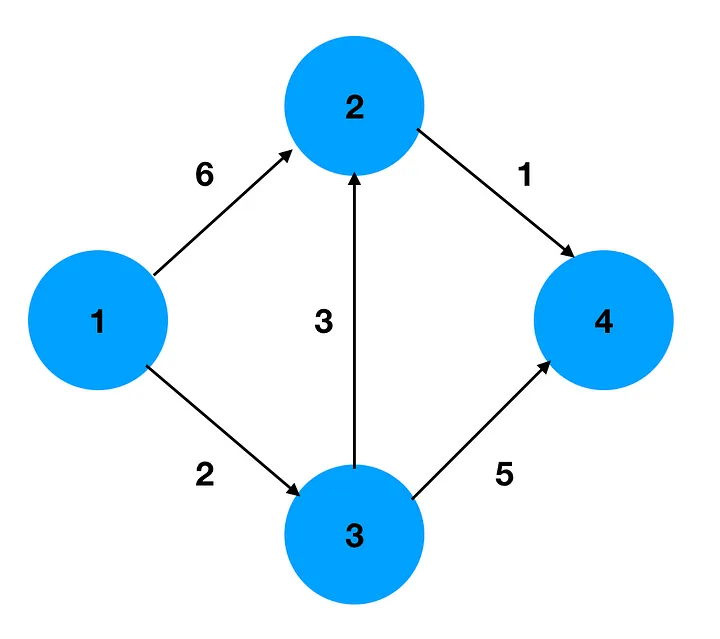
예를 들면

노드1에서 노드2로 가는 비용은 6이고

노드2에서 노드4로 가는 비용은 1이다.

위 그림에서 모든 경로는

경로 - 1 -> 2 -> 4 / 비용(누적) - 6 -> 7

경로 - 1 -> 3 -> 4 / 비용(누적) - 2 -> 7

경로 - 1 -> 3 -> 2 -> 4 / 비용(누적) - 2 -> 5 -> 6

가장 적은 비용으로 이동한 경로는 1 -> 3 -> 2-> 4로 이동한 경로이다.

이 방법은 다익스트라 알고리즘의 구현 중에서 선형 탐색을 이용한 방법이다.

📖 알고리즘의 실질적 활용

📌 최단 경로는 여러 개의 최단 경로로 이루어져있다.

1. 출발 노드에서 도착 노드까지의 비용을 저장한 costs를 만든다.

   • costs에 출발 노드는 0, 나머지는 INFINITY로 채운다.

   • 이유인 즉슨 알지 못하는 값을 INF으로 채워 정보를 업데이트하기 전에 비용 계산에 간섭 여지를 주지 않기 위해서다.

2. 방문했던 노드를 저장할 visited를 만든다.

3. 현재 노드를 나타내는 변수 cur에 출발 노드를 저장한다.

4. cur에서 갈 수 있는 다음 노드 next에 대해 (cur까지의 최단 거리의 비용 + cur -> next의 비용)과 B까지의 최단거리의 비용을 비교한다.

5. 전자가 더 작다면(더 짧은 경로라면) 후자의 값을 전자로 갱신한다.

6. cur의 모든 이웃 노드에 대해 위 작업을 수행한다.

7. cur를 visited에 저장해 방문 완료를 표시한다. 이것으로 이제 cur은 사용되지 않는다.

8. visited에 없는 즉, 방문하지 않은 노드들 중 출발 노드에서 거리가 가장 짧은 노드를 cur로 넣는다.

9. 4 ~ 8 과정을 모든 노드가 방문 완료가 되거나 미방문 노드를 선택할 수 없을 때 까지 반복한다.

마지막 노드에 저장된 값이 출발 노드로부터의 최단 거리이다. 이 값이 INF라면 길이 끊겨있는 것을 의미한다.

아래는 다익스트라 알고리즘을 활용해서 풀어본 문제이다.

📃 문제

여러 개의 도시가 연결된 그래프가 있습니다. 각 도시에는 특정한 비용으로만 이동할 수 있으며, 특정 출발지에서 도착지로 이동할 때 최소 비용을 계산하세요.

⌨ 입력

• N: 도시의 수 (1 ≤ N ≤ 1,000)
• M: 도로의 수 (1 ≤ M ≤ 10,000)
• 도로 정보
  • M개의 줄에 걸쳐 각 줄은 세 정수 u, v, w로 이루어져 있습니다.
  • 이는 도시 u에서 도시 v로 가는 비용이 w임을 의미합니다.
• 시작 도시 S와 도착 도시 E

🔎 예시:
[입력]
N = 5, M = 6
도로 정보:
1 2 2
1 3 3
2 3 2
2 4 4
3 4 1
4 5 2
S = 1, E = 5

💻 풀이

• 우선 순위 큐를 구현하지는 않고 개념만을 이용했기 때문에 시간 복잡도 효율은 좋지 못하다.

function hitTheRoad(n, m, road, s, e) {
  let roadList = Array.from({ length: n + 1 }, () => []);
  let distance = Array(n + 1).fill(Infinity);
  let visited = Array(n + 1).fill(false);

  // 노드의 인접 노드 정보 저장
  road.forEach(([u, v, w]) => {
    roadList[u].push({ node: v, cost: w });
  });

  // 큐 생성 및 초기화
  const queue = [];
  queue.push({ node: s, cost: 0 });
  distance[s] = 0;

  while (queue.length > 0) {
    // 각 노드 최소 비용 정렬
    queue.sort((a, b) => a.cost - b.cost);
    const { node: curNode, cost: curCost } = queue.shift();

    // 방문한 노드 갱신 및 재방문 방지
    if (visited[curNode]) continue;
    visited[curNode] = true;

    // 노드에서 인접 노드 비용 계산
    roadList[curNode].forEach(({ node: nextNode, cost: nextCost }) => {
      const newCost = curCost + nextCost;

      if (newCost < distance[nextNode]) {
        distance[nextNode] = newCost;
        queue.push({ node: nextNode, cost: newCost });
      }
    });
  }
  return distance[e];
}

// 출발 노드 설정
// 출발 노드를 기준으로 각 노드의 최소 비용을 저장
// 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
// 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신
// 위 과정을 반복
const n = 5,
  m = 6,
  s = 1,
  e = 5;
const road = [
  [1, 2, 2],
  [1, 3, 3],
  [2, 3, 2],
  [2, 4, 4],
  [3, 4, 1],
  [4, 5, 2],
];

console.log(hitTheRoad(n, m, road, s, e)); // 6