📘 브루트 포스 (무차별 대입 검색)

📖 개요

📃 브루트 포스는 완전 탐색 알고리즘

• 가능한 모든 경우의 수를 모두 탐색하면서 요구 조건에 충족되는 결과만 가져온다.

• 구현하기 간단하고 솔루션이 존재하는 경우 항상 솔루션을 찾는다.

• 구현 비용(시간복잡도,공간복잡도 등)은 후보 솔루션이 비례한다. -> 규모가 작은 문제에만 사용

• 처리 속도보다는 구현의 단순성이 더 중요할 경우 사용한다.

📃 종류

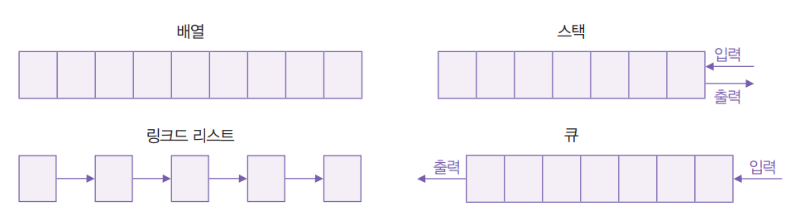
• 선형 구조 전체를 탐색하는 순차 탐색

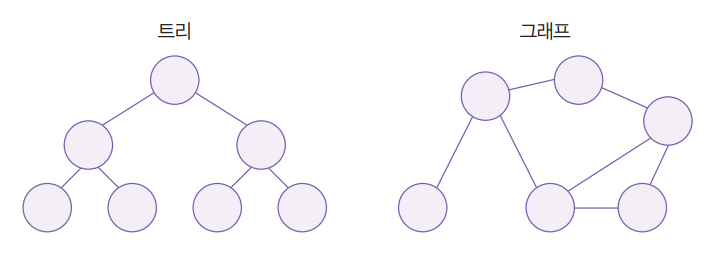
• 비선형 구조를 전체적으로 탐색하는 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS)
  

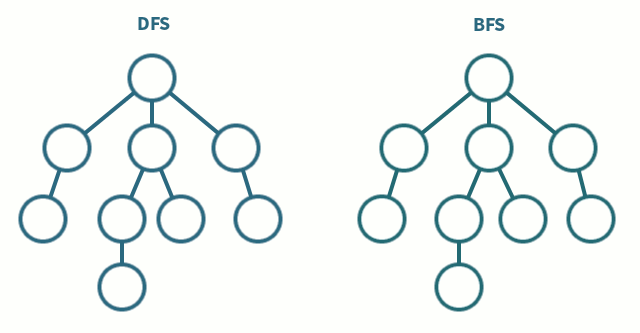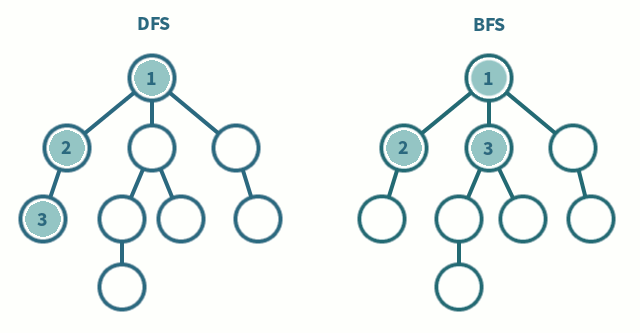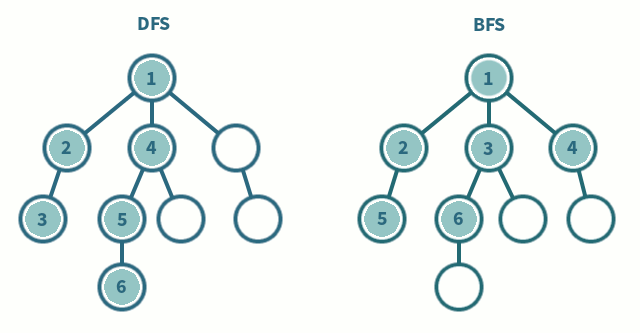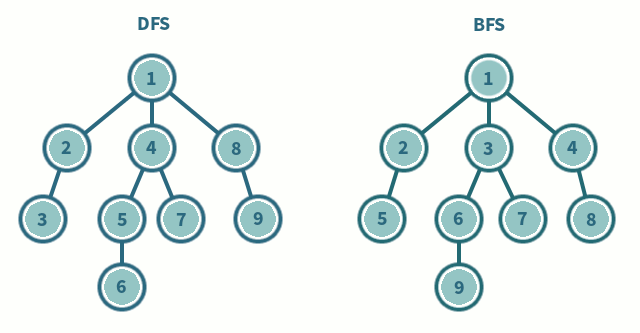
  • 깊이 우선 탐색(Deep first search)

    • 노드에서 다음 분기로 넘어가기 전에 해당 분기를 끝까지 탐색하는 방법

    • 보통 스택과 재귀로 구현

    • 해가 없을 경우 스택오버플로우에 빠질 수 있다. (무한 루프)

    • 목표 노드가 깊을 경우 사용

  • 너비 우선 탐색(Breath first search)

    • 노드에서 단계별로 횡방향으로 탐색하는 방법

    • 보통 큐로 구현

    • 목표 노드가 깊을 경우 DFS에 비해 많은 공간복잡도를 요구한다.

    • 최단 경로를 찾는 다익스트라에도 활용된다.(그래프에 가중치가 없는 경우)

    • 스택으로 구현하는 DFS와 구조가 매우 유사하다.

📖 실질적 활용

📃 순차 탐색

학생들의 번호를 나타내는 정수 배열 number가 매개변수로 주어질 때, 학생들 중 삼총사를 만들 수 있는 방법의 수를 return 하도록 solution 함수를 완성하세요.

• 삼총사 = 3명의 학생의 번호의 합이 0인 경우

function solution(number) {
    let answer = 0;
    for (let i = 0; i < number.length - 2; i++) {
        for (let j = i+1; j < number.length; j++) {
            for (let k = j+1; k < number.length; k++) {
                
                if (number[i]+number[j]+number[k] == 0) {
                    answer++
                }
            }
        }
    }
    return answer;
}

📃 깊이 우선 탐색

n개의 음이 아닌 정수들이 있습니다. 이 정수들을 순서를 바꾸지 않고 적절히 더하거나 빼서 타겟 넘버를 만들려고 합니다. 예를 들어 [1, 1, 1, 1, 1]로 숫자 3을 만들려면 다음 다섯 방법을 쓸 수 있습니다.

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

사용할 수 있는 숫자가 담긴 배열 numbers, 타겟 넘버 target이 매개변수로 주어질 때 숫자를 적절히 더하고 빼서 타겟 넘버를 만드는 방법의 수를 return 하도록 solution 함수를 작성해주세요.

function solution(numbers, target) {
    let answer = 0;
    // 스택 방식 사용
    const stack = [{ idx: 0, sum: 0 }];
    
    // 스택이 빌 때 까지
    while (stack.length > 0) {
        
        const { idx, sum } = stack.pop();
        
        // 모두 순회한 경우
        if (idx === numbers.length) {
            // 합이 타겟 넘버와 일치하면
            if (sum === target) {
                answer++;
            }
        } else {
            // 현재 인덱스의 값을 더하는 경우
            stack.push({ idx: idx + 1, sum: sum + numbers[idx] });
            // 현재 인덱스의 값을 빼는 경우
            stack.push({ idx: idx + 1, sum: sum - numbers[idx] });
        }
        
    }
    return answer;
}

📃 너비 우선 탐색

위와 같은 문제

n이 큰 경우 시간이 매우 많이 걸린다. O(2n)

set을 이용한 중복 제거로 시간을 줄일 수 있다.

function solution(numbers, target) {
    let answer = 0;
    // 큐 방식 사용
    const queue = [{ index: 0, sum: 0 }];

    // 큐가 빌 때까지
    while (queue.length > 0) {
      
        const { idx, sum } = queue.shift();

        // 모든 숫자를 사용한 경우
        if (idx === numbers.length) {
            // 현재 합이 타겟과 같으면 경우의 수 증가
            if (sum === target) {
                answer++;
            }
        } else {
            // 현재 인덱스의 값을 더하는 경우
            queue.push({ index: idx + 1, sum: sum + numbers[idx] });
            // 현재 인덱스의 값을 빼는 경우
            queue.push({ index: idx + 1, sum: sum - numbers[idx] });
        }
    }

    return answer;
}