[머신러닝을 위한 기초수학] - 구분구적법과 정적법

구분구적법과 정적법

1. 구분구적법은 주어진 구간을 여러 개의 작은 구간으로 나누어서, 각각의 작은 구간에서 함수값을 근사적으로 계산한 후 이 값을 더해 정적분 값을 근사하는 방법
   이 방법은 직사각형의 넓이를 계산하여 근사적인 값을 얻으므로, 정확도가 낮을 수 있다.

2. 정적법은 부정적분을 이용하여 원래의 함수를 다른 함수로 치환한 후, 적분을 수행하는 방법
   이 방법은 원래 함수를 구할 수 있다면 정확한 값으로 적분을 수행할 수 있으므로,
   구분구적법보다 정확도가 높다.

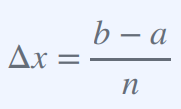
Δx = (b - a) / n 은 구간 [a, b]를 n 등분하여 한 구간의 길이인 Δx를 계산하는 공식

여기서,
1) a와 b는 구간의 시작점과 끝점입니다.
2) n은 구간을 등분하는 개수이며, n이 클수록 구간의 등분이 미세해지고 Δx가 작아져서 구분구적법의 정확도가 향상된다.
3) Δx는 구간 [a, b]를 n 등분한 각 구간의 길이를 의미

예를 들어, 구간 [0, 4]를 8 등분하여 구분구적법을 적용하려고 할 때, Δx = (4 - 0) / 8 = 0.5 가 된다.
따라서, 각 등분된 구간의 길이는 0.5이며, 이를 이용하여 각 구간에서의 함수값을 근사적으로 계산하여 적분 값을 근사할 수 있다!

아래는 정말 잘 정리되어 있는 블로그 링크!
https://post.naver.com/viewer/postView.nhn?volumeNo=14462772&memberNo=8076928