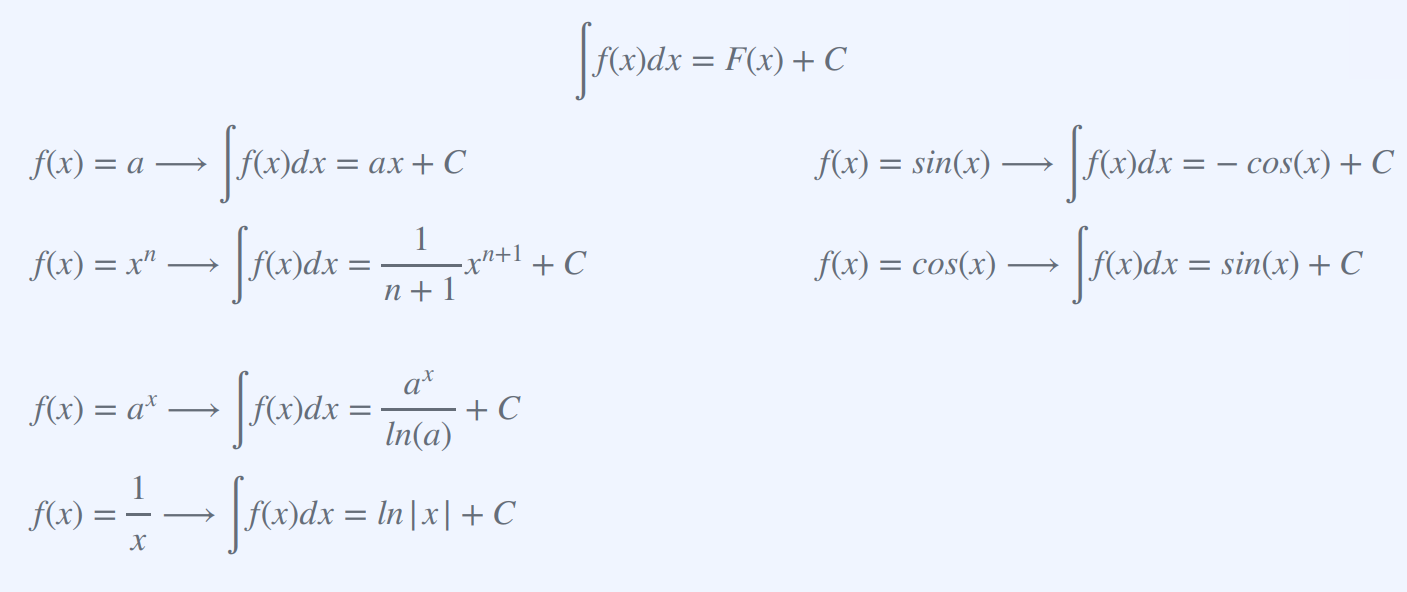[머신러닝을 위한 기초수학] - 적분공식과 부정적분

부정적분이란 미분과 반대되는 개념으로, 주어진 함수의 원래 함수를 찾는 것.
적분은 함수의 기울기를 찾아내는 미분과 반대로 함수의 면적을 구하는 것!

1. 적분 공식

1. 기본적분 공식: ∫ x^n dx = (x^(n+1))/(n+1) + C (단, n ≠ -1)

2. 삼각함수 적분 공식: ∫ sin(x) dx = -cos(x) + C , ∫ cos(x) dx = sin(x) + C

3. 지수함수 적분 공식: ∫ e^x dx = e^x + C

4. 로그함수 적분 공식: ∫ (1/x) dx = ln|x| + C

5. 역삼각함수 적분 공식: ∫ (1/√(1-x^2)) dx = arcsin(x) + C, ∫ (1/√(1+x^2)) dx = arctan(x) + C

2. 적분 규칙

1. 선형성: ∫ (af(x) + bg(x)) dx = a∫f(x) dx + b∫g(x) dx

2. 치환법: ∫ f(g(x))g'(x) dx = ∫ f(u) du (단, u = g(x))

3. 부분적분: ∫ u dv = uv - ∫ v du

3. 미적분학의 기본 정리

f(x)를 구간 [a, b]에서 연속인 함수라고 할 때, 다음 두 가지 결과가 성립한다.

1. f(x)의 부정적분을 F(x)라고 하면, F(x)는 [a, b]에서 f(x)의 어떤 원시함수(primitive function)이다.
   즉, F(x)는 f(x)의 면적을 누적한 함수이며, F'(x) = f(x)가 성립한다.

2. f(x)를 [a, b]에서 적분한 값은 다음과 같이 구할 수 있다.
   ∫ a ~ b f(x) dx = F(b) - F(a)

즉, f(x)의 면적을 [a, b]에서 구한 후, F(b)와 F(a)를 뺀 값과 같다.

이 정리는 미분과 적분이 서로 역함수 관계에 있다는 것을 나타내므로, 미분과 적분의 계산을 상호보완적으로 할 수 있도록 도와준다.
또한, 이 정리를 통해 함수의 면적을 쉽게 계산할 수 있다.