[머신러닝을 위한 기초수학] - 극한

Limits 극한

1. x가 a에 접근할 때 f(x)가 L에 접근한다.
2. 하지만 x는 절대로 a와 같아지지 않는다.
3. 구체적으로, 임의의 양수 ε에 대해, |x-a| < δ인 경우 |f(x) - L| < ε가 되도록 양수 δ가 존재한다.
   

좌극한과 우극한 (Left / Right-hand Limits)

• 함수 f(x)의 점 a에서의 좌극한은
  "x가 a에서 왼쪽으로 접근할 때 f(x)의 극한" 또는 "x → a⁻로 다가갈 때 f(x)의 극한"으로 표시

• 함수 f(x)의 점 a에서의 우극한은
  "x가 a에서 오른쪽으로 접근할 때 f(x)의 극한" 또는 "x → a⁺로 다가갈 때 f(x)의 극한"으로 표시

• 함수 f(x)의 점 a에서의 좌극한과 우극한이 모두 존재하고 서로 같은 경우,
  f(x)가 x가 a에 접근할 때의 극한이 존재하고 이 공통의 값을 가진다고 말한다.

• 그러나 좌극한과 우극한이 서로 다른 경우, 함수 f(x)의 극한이 존재하지 않는다.

즉, 함수가 특정 지점에서 극한을 가진다면, 해당 지점에서 "연속"이라고 한다.
그러나 함수가 특정 지점에서 극한을 갖지 않는다면, 해당 지점에서 "불연속"이라고 한다.

추가개념

1. 구간 내 연속성 :

   함수 f(x)가 닫힌 구간 [x1, x2]에서 모든 점에서 연속적이라면,
   즉 모든 a ∈ [x1, x2]에 대하여 다음이 성립한다면:

   lim f(x) = f(a)
   x → a

   여기서 x가 a에 왼쪽과 오른쪽에서 접근할 때 f(x)의 극한이 존재하고 f(a)와 같다는 것을 의미
   만약 이 조건이 구간 [x1, x2]의 모든 점 a에 대해서 성립한다면, 함수 f(x)는 구간 [x1, x2]에서 연속적

2. 점에서 연속성 :

   함수 f(x)가 정의역 D에서 a 지점에서 연속이라면,
   즉 다음이 성립한다면:

   lim f(x) = f(a)
   x → a

   여기서 x가 a에 접근할 때 f(x)의 극한이 존재하고 f(a)와 같다는 것을 의미
   이것은 함수 f(x)가 a에서 갑작스런 변화나 점프 없이 부드럽게 변화하며, 펜을 종이에서 떼지 않고 a에서 그릴 수 있다는 것을 의미
   이 조건이 정의역 D의 모든 점 a에 대해서 성립한다면, 함수 f(x)는 정의역 D에서 연속적이라고 말한다.
   

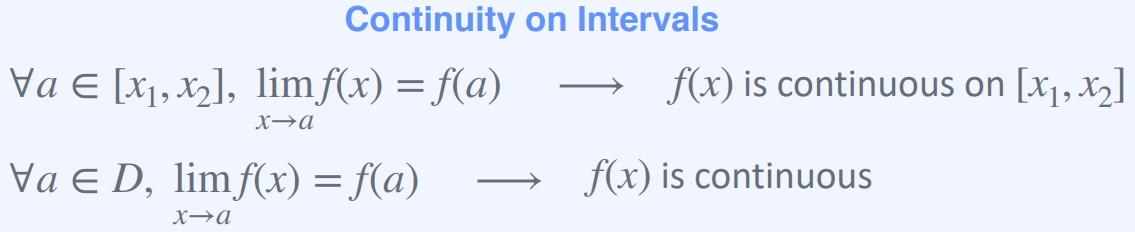
3. 수평접선(horizontal asymptotes) :

   수평접선은 함수가 어떤 값에 접근할 때 함수 값이 수평선에 접근하는 현상을 말한다.
   예를 들어, 함수 f(x)가 x가 양의 무한대로 가면서 0으로 수렴하는 경우, 이 함수는 y = 0에 대해 수평접선을 가진다. (즉, 미분 계수가 0이다.)

   일반적으로, 함수 f(x)가 x가 양의 무한대로 가면서 L로 수렴하거나 x가 음의 무한대로 가면서 L로 수렴하는 경우, 이 함수는 y = L에 대해 수평접선을 가집니다. 이때, L은 수평접선의 방정식

   수평접선을 가지는 함수는 극한이 존재하며, 수평접선의 위치는 극한값과 일치

4. 수직접선(vertical asymptotes) :

   수직 접선은 함수 f(x)가 어떤 값 x = a에서 발산(infinite)할 때 나타난다.
   보통 분모가 0이 되거나, 로그 함수의 정의역에서 0이 될 때, 또는 지수 함수의 정의역에서 음수가 되는 경우가 대표적

   이러한 경우에 함수는 무한대로 발산하기 때문에 그래프는 수직 방향으로 무한히 증가하거나 감소하게 된다.'

   이 때, 그래프는 x=a에서 수직선에 수렴(converge)하며, 이를 수직 접선이라고 한다.