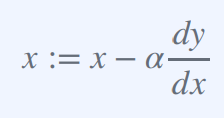평균변화율 (Average Rates of Change) / 순간변화율(Instantaneous Rates of Change)

출처 : https://www.youtube.com/watch?v=VNwTmjYMJ7A
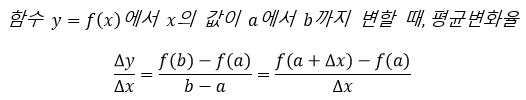
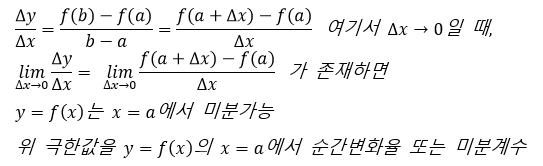
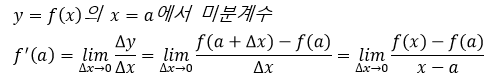
즉, 미분계수(Differential Coefficients) = 접선의 기울기 = 그 점에서의 순간 변화율
- 어떠한 함수 y=f(x)에 대해 x=a에서 미분 가능하다면 f'(a)를 미분계수라고 정의
만약, 미분계수가 함수처럼 나타나 있다면? 그것을 바로 도함수라 한다.
(미분계수와 도함수의 차이는 함수의 형태를 하고 있느냐 없느냐의 차이)
도함수는 함수의 기울기, 변화율, 최대값, 최소값 등의 정보를 추출하는 데에 유용하게 사용된다.
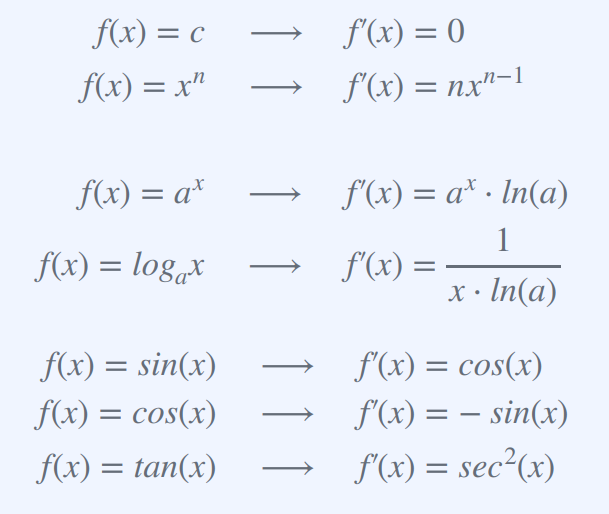
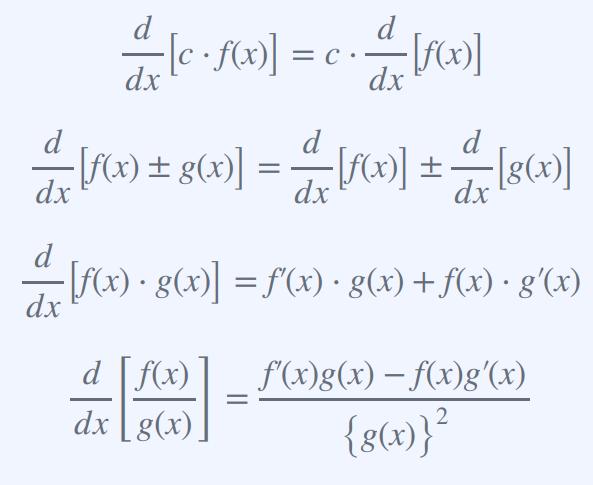
Chain Rule 체인룰 : 합성함수의 도함수를 구하는 데 사용되는 기본적인 규칙 중 하나
합성 함수 f(g(x))의 도함수가 외부 함수의 도함수 f'(g(x))와 내부 함수의 도함수 g'(x)의 곱으로 주어진다는 것을 말한다.
즉, (d/dx)[f(g(x))] = f'(g(x)) * g'(x)
예를들어,
함수 h(x) = (x^2 + 1)^3을 살펴보자!
이 함수는 두 개의 함수 f(x) = x^3과 g(x) = x^2 + 1의 합성으로 볼 수 있다.
연쇄 법칙(체인룰)을 적용하여 h(x)의 도함수를 구할 수 있다.
h'(x) = f'(g(x)) g'(x) = 3(g(x))^2 2x = 6x(x^2 + 1)^2
경사 하강법(Gradient Descent) : x := x − α dy/dx
위 식에서 α는 학습률(learning rate) dy/dx는 손실 함수 f(x)의 x에 대한 편미분값을 의미한다.
경사 하강법은 기울기가 가장 가파른 방향으로 계속 이동하며
손실 함수를 최소화하는 값을 찾는 최적화 알고리즘이다.
위 식은 현재 x 값에서 기울기(dy/dx)와 학습률(α)을 곱한 값을 현재 x 값에서 빼는 것으로,
새로운 x 값이 업데이트된다.
이러한 과정을 손실 함수가 최소값을 갖을 때까지 반복한다.
참고) :=는 대입 연산자를 나타내며, 오른쪽의 값을 왼쪽의 변수에 대입한다.

출처 : https://heung-bae-lee.github.io/2019/12/08/deep_learning_02/
추가개념)
경사 하강법은 다음과 같은 과정으로 이루어진다.
1) 초기값 설정: 경사 하강법을 시작하기 위해, 최적화하고자 하는 함수의 변수들의 초기값을 설정한다.
2) 기울기 계산: 초기값으로부터 함수의 기울기를 계산합니다. 이를 위해서는 각 변수들에 대한 편미분을 계산한다.
3) 업데이트 규칙 적용: 기울기와 학습률(learning rate)을 곱한 값을 현재 변수 값에서 빼는 방식으로 변수 값을 업데이트함. 이를 반복하여 함수의 최솟값을 찾는다.
4) 종료 조건 확인: 일정 횟수나 일정한 기준에 도달하면 알고리즘을 종료한다.
학습률은 변수 값을 업데이트할 때 얼마나 크게 변화시킬지를 결정하는 하이퍼파라미터로,
적절한 값을 선택하는 것이 중요하다.
학습률이 너무 작으면 수렴 속도가 느리고, 너무 크면 최솟값을 찾지 못하고 발산하는 문제가 발생할 수 있다.
경사 하강법은 함수의 모양에 따라서 최적화가 잘 되지 않을 수 있다.
만약 함수가 복잡한 형태를 가지고 있거나 로컬 최솟값(local minimum)이 많은 경우, 알고리즘이 전역 최솟값(global minimum)을 찾지 못하고 로컬 최솟값에 수렴할 가능성이 있다.
이를 해결하기 위해서는 초기값 설정이나 학습률 조정 등의 방법을 사용할 수 있다.