
샤논 정보량(Shannon Information) 또는 샤논 엔트로피(Shannon entropy)
: 확률 분포에서의 불확실성 또는 무작위성의 정도를 측정하는 방법 중 하나
사건 A의 샤논 정보량은 I(P(A))로 표기되며, A의 확률의 음의 로그로 정의된다.
I(P(A)) = -log(P(A))
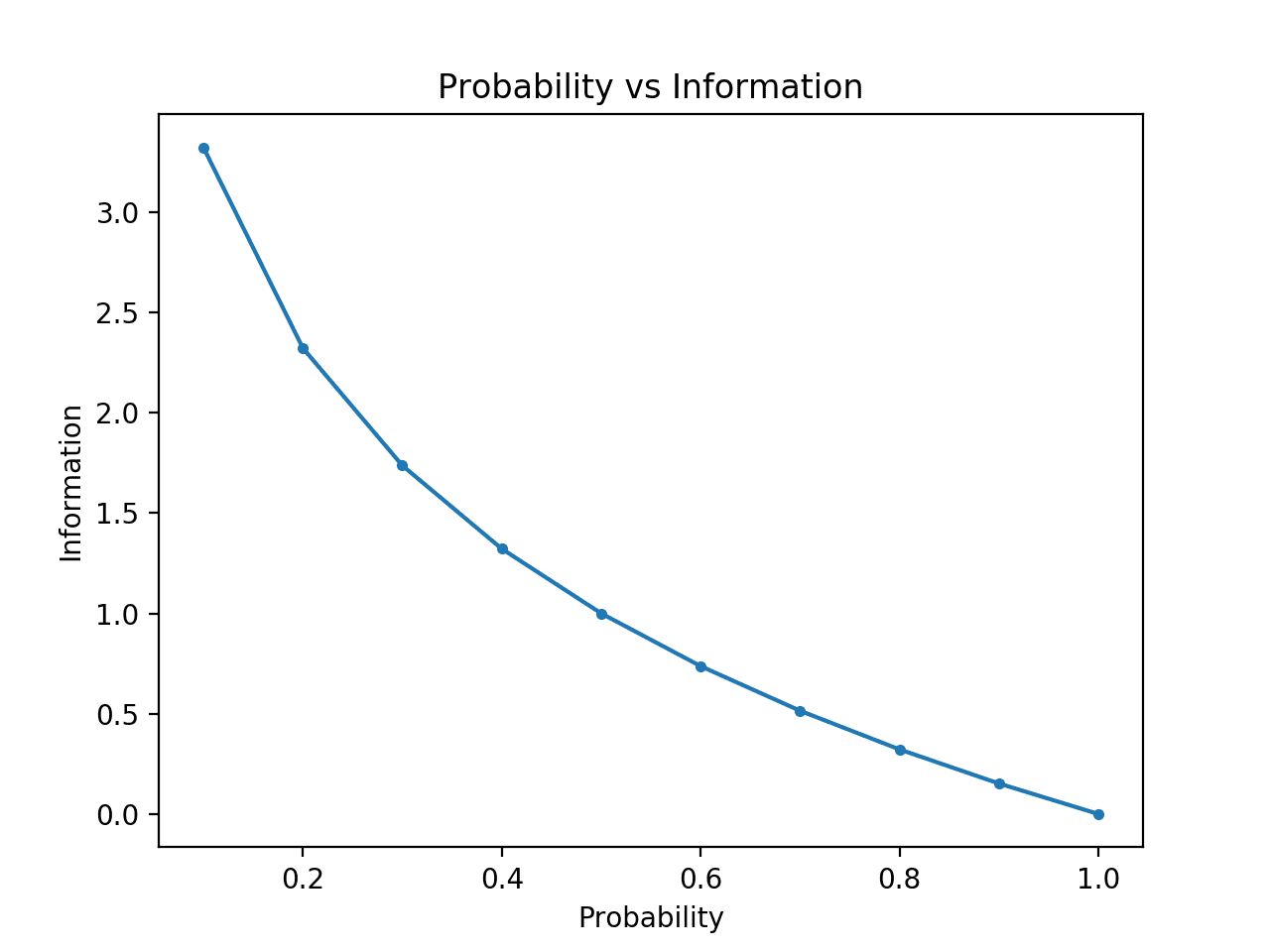
샤논 정보량은 확률이 0에 가까워질수록 증가하는 0 이상의 양수이다.
즉, 사건이 더욱 불확실할수록, 발생할 때 더 많은 정보를 제공한다.
반면에, 사건이 반드시 발생할 확률이 1인 경우에는 전혀 정보를 제공하지 않는다.
샤논 정보량은 암호학, 데이터 압축, 그리고 머신 러닝 등의 분야에서 널리 사용되며,
신호나 데이터 집합의 정보 내용을 측정하는 데 사용될 수 있다.
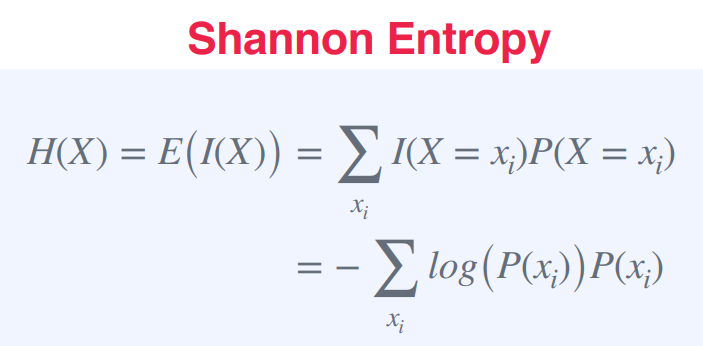
확률 변수 X에 대한 Shannon Entropy는 다음과 같이 정의된다.
H(X) = E(I(X)) = Σ I(X = xi)P(X = xi)여기서, I(X = xi)는 확률 변수 X가 xi값을 가질 때 정보의 양을 나타내는 Shannon Information이고,
P(X = xi)는 X가 xi값을 가질 확률이다.
Shannon Information을 이용하여 계산된 Shannon Entropy는 X의 분포에서의 불확실성 또는 엔트로피를 측정한다.
즉, Shannon Entropy가 높을수록 X의 분포가 더 불확실하거나 더 예측하기 어렵다는 것을 의미!
Shannon Entropy는 다음과 같은 식으로도 표현될 수 있다.
H(X) = - Σ P(xi) log(P(xi))여기서, P(xi)는 X가 xi값을 가질 확률
이 식에서는 Shannon Information의 정의를 이용하여 Shannon Entropy를 간단히 표현하고 있다.
정리)
Shannon 엔트로피(H)는 확률 분포에서의 불확실성이나 무질서 정도를 나타내는 지표로
무작위 변수 X에 포함된 "놀라움"이나 "정보"의 양을 알려준다.
X의 Shannon 엔트로피를 계산하려면, 먼저 X의 각 가능한 결과 xi의 Shannon 정보를 계산해야함
xi의 Shannon 정보는 P(xi)가 xi의 확률일 때, -log(P(xi))로 정의된다.
그런 다음 X의 모든 가능한 결과에 대해 Shannon 정보의 기댓값을 구한다.
이 기댓값은 X의 Shannon 엔트로피이며, H(X)로 표기된다.
다시 말해, X의 Shannon 엔트로피는 X의 각 가능한 결과의 확률과 해당 Shannon 정보의 곱의 합으로 계산된다. 이는 각 결과의 로그와 확률의 곱의 부정수 합으로도 작성할 수 있다.
이 공식은 복잡해 보일 수 있지만, 본질적으로 확률 분포에서 얼마나 많은 불확실성이 있는지를 양적으로 나타내는 방법이다.
엔트로피가 높을수록 분포는 예측하기 어려워지며, 분포가 몇 가지 결과에 집중될수록 엔트로피는 낮아진다. 분포의 모든 결과가 동일한 확률을 가질 때 엔트로피는 최대값을 가진다.
H(X)는 X에 대한 정보의 기댓값!
Shannon Information을 각각의 확률값으로 가중평균한 것이 H(X)가 되므로,
각 확률값이 정보의 "기여도"를 나타내게 된다.
따라서 H(X)는 X의 불확실성 혹은 무질서도를 나타내는 값으로,
X의 분포가 얼마나 예측하기 어려운지를 측정하는 지표!Binary Entropy
이항 분포에서 나오는 확률 변수 X의 확률 분포에 대한 Shannon entropy(불확실성)를 계산한 것
이항 분포에서 X가 1일 확률이 p이므로, X가 0일 확률은 1-p이다.
따라서 Shannon entropy의 공식을 이에 맞게 적용하면 아래와 같다.
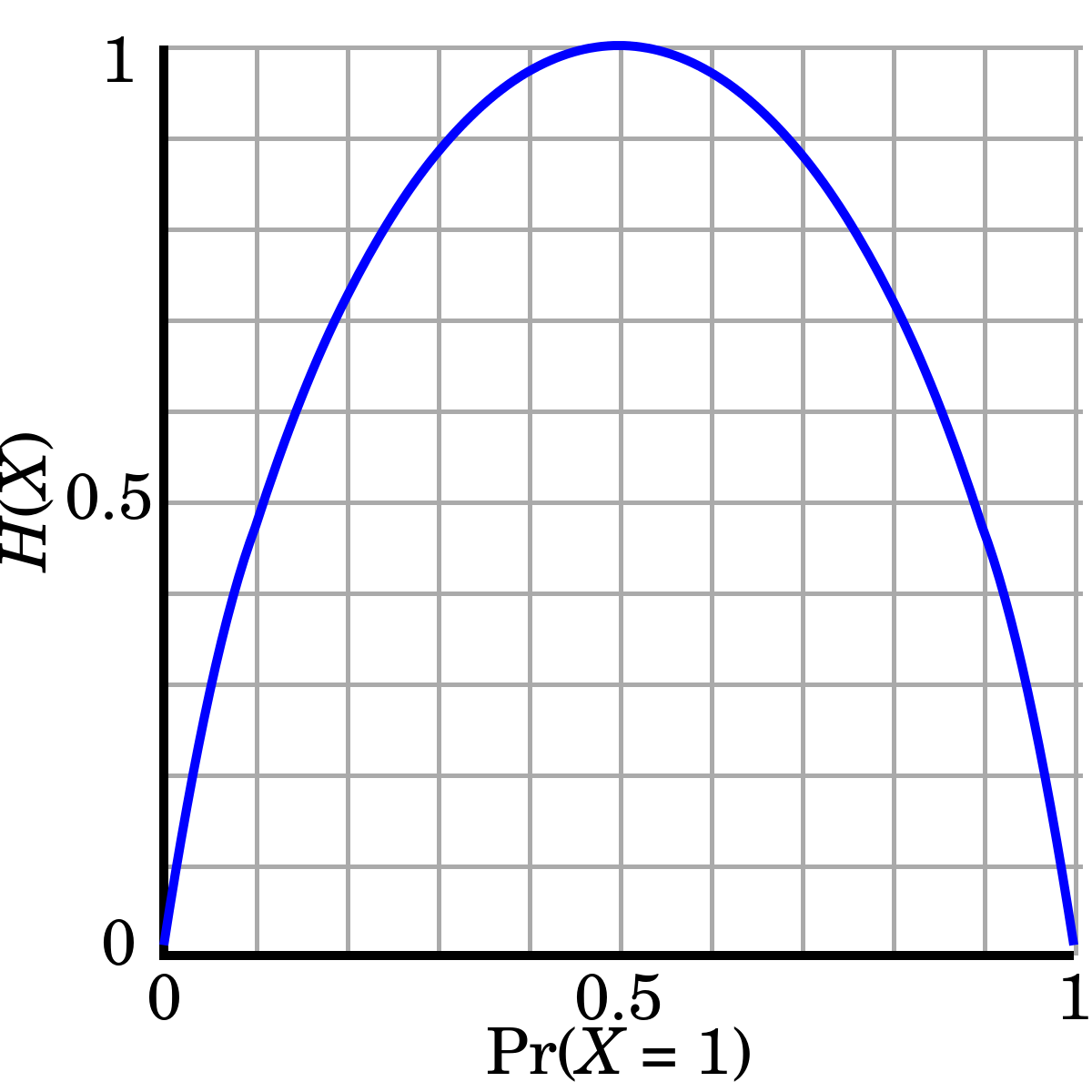
H(X) = - [plog(p) + (1 - p)log(1 - p)]두 가능한 결과가 있으므로 확률은 합쳐서 1이어야 한다.
위 공식은 하나의 이항 결정에 포함된 정보 또는 엔트로피의 양을 나타낸다.
만약 p=0.5라면, 이벤트 X=1이 X=0과 동일한 확률로 발생하기 때문에 이항 엔트로피는 최대값을 가진다.
이것은 결정이 가장 불확실하고, 가장 많은 정보를 제공한다는 것을 의미한다.
만약 p=0 또는 p=1이면, 불확실성이 없으므로 이항 엔트로피는 0이다.
예를 들어, 동전이 0.8의 확률로 앞면(X=1)이 나오고, 0.2의 확률로 뒷면(X=0)이 나온다면,
이항 엔트로피는 다음과 같이 계산할 수 있다
B(X) = -[0.8 log2(0.8) + 0.2 log2(0.2)]
≈ 0.7219이 값은 동전을 던졌을 때 포함된 정보의 양을 나타낸다.
이 경우 동전은 편향되어 있기 때문에 던지기 전에는 많은 정보를 제공한다.
만약 동전이 공평하다면, 이항 엔트로피는 최대값을 가지며, 던지기 전에 가장 많은 정보를 제공한다.

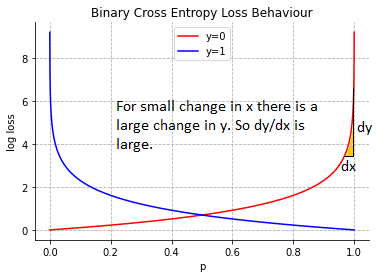
Binary Cross Entropy (또는 Binary Log Loss) : 분류 모델의 손실 함수 중 하나
이 함수는 실제 값과 예측 값이 0 또는 1인 이진 분류 문제에서 사용된다.
J = − [ylog(ŷ) + (1 − y)log(1 − ŷ)]여기서 y는 실제 값 (0 또는 1)이고, ŷ는 모델의 예측 값(0과 1 사이의 확률값)이다.
이 함수는 모델이 예측한 확률 값이 실제 값과 얼마나 차이 나는지를 나타낸다.
수식에서 첫 번째 항은 y=1일 때의 손실, 두 번째 항은 y=0일 때의 손실을 계산한다.
이 값을 최소화하면 모델이 더 정확한 예측을 할 수 있다!
이 함수는 모델이 예측한 값이 실제 값과 일치할 때 손실이 최소가 된다.
즉, 모델이 정확하게 예측할수록 손실이 작아진다.
예를 들어, 이진 분류 모델이 스팸 메일을 예측하는 문제에서 Binary Cross Entropy를 사용할 수 있다.
모델이 스팸 메일인 것으로 예측한 메일의 ŷ값이 0.8이고, 이 메일이 실제로 스팸 메일인 경우 y값은 1이다.
이 경우 Binary Cross Entropy는 다음과 같이 계산된다.
J = − [1log(0.8) + (1 − 1)log(1 − 0.8)] ≈ 0.223이 값은 모델이 스팸 메일을 예측하는 데 얼마나 잘 수행되는지에 대한 척도로 사용된다.
더 높은 값은 모델의 성능이 더 나쁘다는 것을 의미하고, 낮은 값은 모델이 더 나은 예측을 한다는 것을 의미한다.
결론) 스팸 필터링 같은 이진 분류 문제에서 모델이 스팸 메일인 경우를 1로, 스팸이 아닌 경우를 0으로 예측하는 경우에 적합!
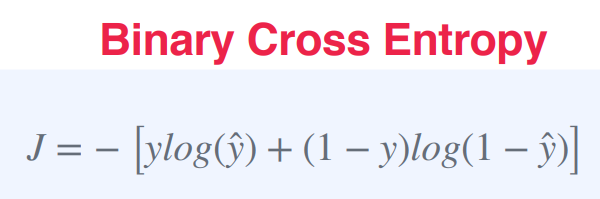
Cross Entropy 교차 엔트로피
: 예측 확률 분포와 라벨 집합의 실제 분포를 비교하는 데 사용되는 두 확률 분포의 차이를 측정하는 지표
J = - ∑ y*log(ŷ)여기서 y는 실제 분포를, ŷ는 예측 분포를 나타낸다
합산은 분포의 모든 카테고리(또는 클래스)에 대해 이루어진다.
교차 엔트로피는 종종 입력을 여러 카테고리 중 하나로 분류하는 모델의 학습을 위한 손실 함수로 사용된다.
학습 프로세스의 목표는 예측된 확률 분포와 라벨의 실제 분포 간의 교차 엔트로피를 최소화하는 것이다!
다시 말해, 라벨이 알려진 일련의 학습 예제가 있다면, 우리는 예측된 분포와 실제 분포 간의 교차 엔트로피 손실을 최소화함으로써 새로운 예제의 라벨을 예측하는 모델을 훈련시킬 수 있다.
예를 들어, 각 예제를 0 또는 1로 라벨링할 수 있는 이진 분류 문제가 있다고 가정해보자!
실제 라벨이 1이면 실제 분포 y는 [0, 1]이 되며, 예측된 분포 ŷ는 [ŷ0, ŷ1]이 된다.
이 예제의 교차 엔트로피 손실은 다음과 같다.
J = - (0log(ŷ0) + 1log(ŷ1))
= -log(ŷ1)예측된 확률 ŷ1이 1에 가까울수록 손실은 작아지며, 모델이 올바른 라벨을 높은 신뢰도로 예측하고 있음을 나타낸다.
예측된 확률 ŷ1이 0에 가까울수록 손실은 커지며, 모델이 높은 신뢰도로 잘못된 라벨을 예측하고 있음을 나타낸다.

