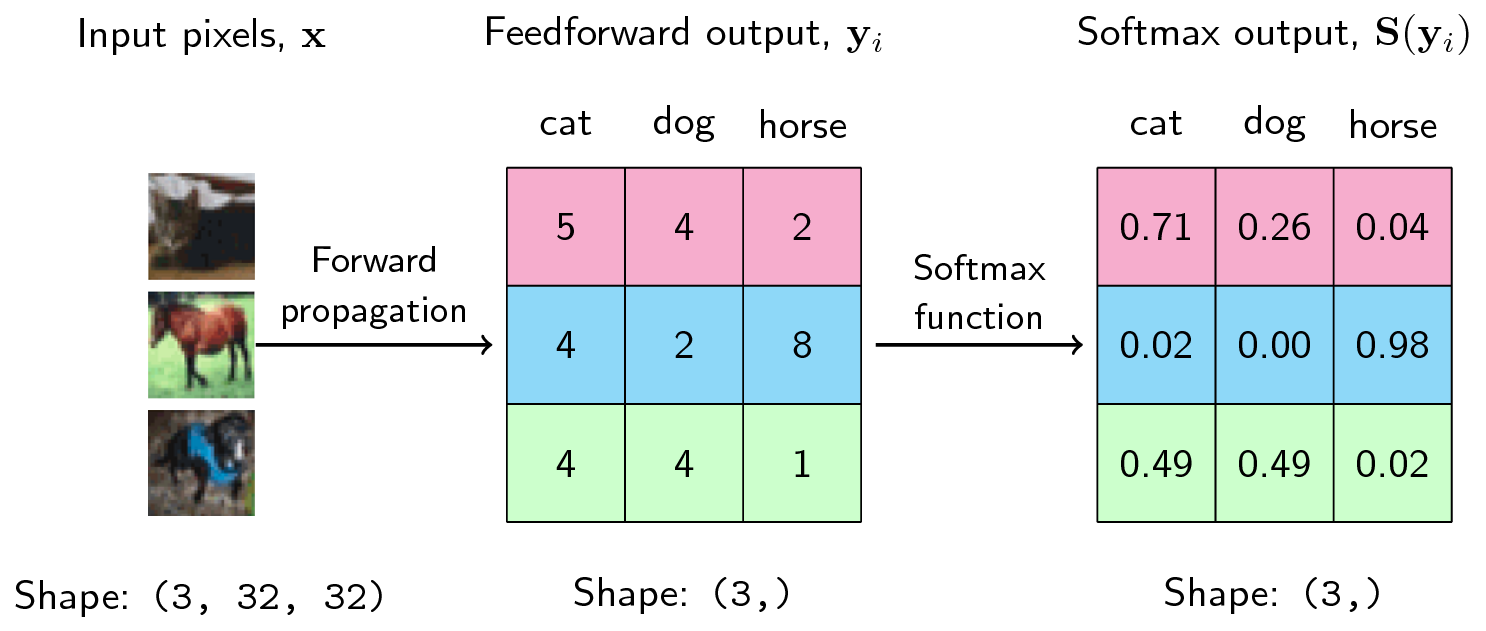
로짓(logit) : 어떤 사건의 성공 확률을 나타내는 P(A)와 실패 확률을 나타내는 1-P(A)의 비율의 로그값
어떤 사건 A의 확률값 P(A)를 실수값인 로짓(logit) 또는 로그 오즈(log-odds) 값으로 매핑한다.
구체적으로, 어떤 사건 A의 확률값 P(A)가 주어졌을 때, 로짓은 다음과 같이 계산 가능하다.
logit(A) = log(P(A) / (1 - P(A)))
즉, 확률을 받아 로짓값으로 만들어준다고 생각하자!결과적으로 얻어지는 로짓 값은 실수값이므로 0에서 1까지의 확률값을 모델링할 때 유용하다.
즉, 로짓은 성공 확률 P(A)와 실패 확률 1-P(A)의 비율을 나타내므로, 어떤 사건에 대한 로짓 값이 양수인 경우에는 해당 사건이 성공할 확률이 50%보다 높은 것으로 해석 가능!
마찬가지로 로짓 값이 음수인 경우에는 해당 사건이 실패할 확률이 50%보다 높은 것으로 해석할 수 있다.
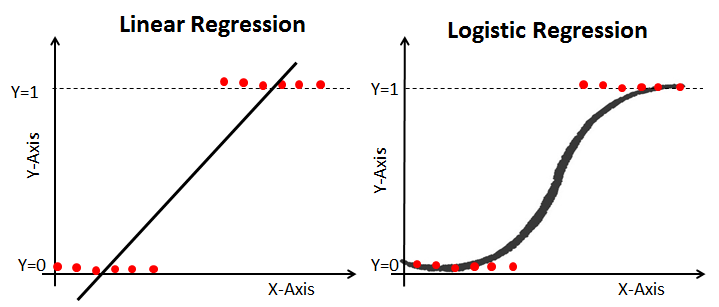
로짓 함수는 로지스틱 회귀(logistic regression)와 같은 분류 알고리즘에서 사용된다.
로지스틱 회귀는 입력값과 가중치의 선형 결합을 로짓 함수에 적용한 결과를 시그모이드 함수(sigmoid function)를 통해 확률값으로 변환한다.
이렇게 변환된 확률값을 기반으로 분류 결정을 내리게 됨!
참고) 로지스틱 함수는 로짓 함수의 역함수이며, 로짓 값으로부터 원래의 확률값을 계산하는 함수

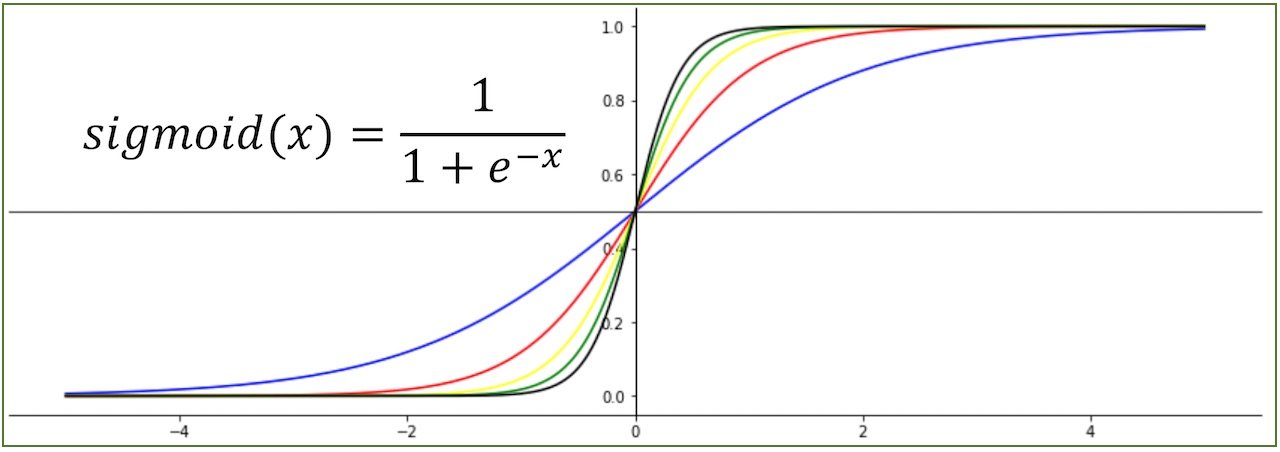
시그모이드(sigmoid) 함수 : 어떤 실수 값이든 0과 1 사이의 값을 매핑
입력값을 확률 값으로 변환하는 역할!
시그모이드 함수는 S자 형태의 곡선을 가지는 비선형 함수로,
어떤 입력값에 대해서도 0과 1 사이의 값으로 출력한다.
σ(x) = 1 / (1 + e^(-x))
즉, logit을 받아 확률로 바꿔준다고 생각하자!로짓 함수와 시그모이드 함수의 관계는 시그모이드 함수가 로짓 함수의 역함수라는 것!
구체적으로, 시그모이드 함수를 사용하여 로짓 값을 확률 값으로 변환할 수 있다.
P(x) = 1 / (1 + e^(-logit(x)))여기서 x는 입력값을 의미
시그모이드 함수의 출력값은 입력값 x에 따라 달라지며, x가 양수일수록 1에 가까워지고, 음수일수록 0에 가까워진다.
x가 0일 때는 함수값이 0.5가 됨!
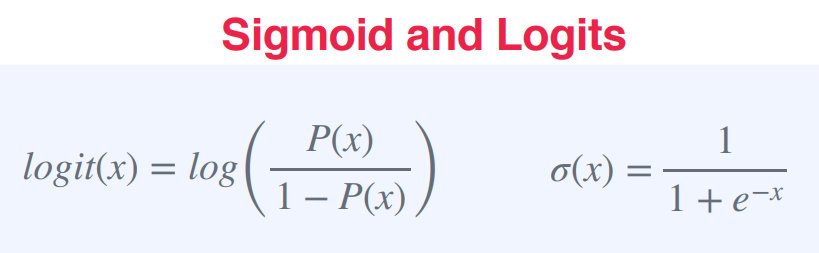
Probability Vector and Softmax (확률 벡터와 소프트맥스 함수)
확률 벡터는 각 클래스에 속할 확률을 벡터로 나타낸 것
벡터의 각 요소는 0과 1 사이의 값을 가지며, 모든 요소의 합은 1이다.
예를 들어, 세 개의 클래스 A, B, C가 있을 때, 확률 벡터 [0.3, 0.4, 0.3]은 클래스 A에 속할 확률이 0.3,
클래스 B에 속할 확률이 0.4, 클래스 C에 속할 확률이 0.3임을 나타낸다.
소프트맥스 함수는 각 입력값을 확률 값으로 변환하는 함수이다.
입력값을 벡터로 나타낸 경우, 소프트맥스 함수는 벡터의 각 요소를 0과 1 사이의 값으로 변환하고,
변환된 값의 합이 1이 되도록 정규화한다.
소프트맥스 함수 : St(l) = e^lt / ∑C_i=1 e^li여기서 l은 입력 벡터의 인덱스를 나타내며, t는 임의의 상수를 의미
함수의 출력값은 입력 벡터의 각 요소를 확률 값으로 변환한 확률 벡터이다.
소프트맥스 함수는 로지스틱 회귀 등의 분류 모델에서 활성화 함수로 사용되며, 입력값을 확률 값으로 변환하는 역할을 한다.
또한, 신경망에서 출력값을 확률 값으로 변환하는 데에도 사용된다.
추가 참고)
확률 벡터는 여러 가능한 결과 중에서 각 결과가 나타날 확률을 나타내는 벡터이다.
예를 들어, 주사위를 굴려 나올 수 있는 6가지 결과를 고려해보자
각 결과에 대해 1/6의 확률을 할당할 수 있으며, 이를 벡터로 표현하면 다음과 같다.
[1/6, 1/6, 1/6, 1/6, 1/6, 1/6]소프트맥스 함수는 이러한 확률 벡터를 다루는 데에 유용.
소프트맥스 함수는 어떤 벡터를 입력으로 받아, 각 요소를 확률로 해석할 수 있는 벡터로 변환한다.
이를 위해, 입력 벡터의 각 요소를 지수 함수로 변환한 후, 이를 모두 더한 값으로 나누어 각 요소의 상대적인 크기를 유지하면서 전체 합이 1인 확률 벡터를 만든다.
예를 들어, 다음과 같은 벡터를 고려해보자!
[2.0, 1.0, 0.1]이 벡터에 소프트맥스 함수를 적용하면 다음과 같이 계산된다.
St(1) = exp(2.0) / (exp(2.0) + exp(1.0) + exp(0.1)) = 0.659
St(2) = exp(1.0) / (exp(2.0) + exp(1.0) + exp(0.1)) = 0.242
St(3) = exp(0.1) / (exp(2.0) + exp(1.0) + exp(0.1)) = 0.099
결과적으로, 소프트맥스 함수는 다음과 같은 확률 벡터를 반환한다.
[0.659, 0.242, 0.099]