
선형 함수(Linear Functions)
y = ax + b
- 여기서 a와 b는 상수
- x는 독립 변수이고, y는 종속 변수
- a는 기울기(slope)를 나타내고, b는 y절편(y-intercept)을 나타냄
- 선형 함수의 그래프는 직선 >> 일직선 모양
- 또한 x의 차수가 1차이기 때문에 다항식 함수(polynomial function)의 일종
-> 일반적으로 x가 1차항으로 들어가 있고, 상수항 b가 있기 때문에 1차 함수로도 불림
Power Functions
y = x^n
g(x) = x^n
예를 들어
n = 2인 경우, y = x^2는 포물선 모양인 이차 함수가 된다.
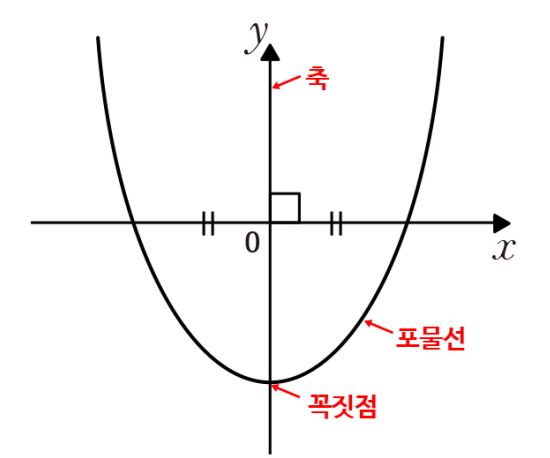
n = 1/2인 경우, y = √x는 원점에서 시작하여 서서히 증가하는 곡선인 제곱근 함수가 된다.
n = -1인 경우, y = 1/x는 초형 모양인 역함수가 된다.
Power functions은 인구 증가, 방사성 물질의 붕괴, 유체의 흐름 등 많은 자연 현상을 모델링하는 데 사용
또한 신호 처리, 이미지 분석, 데이터 압축 등 많은 공학 및 과학적 응용 분야에서도 사용된다.
상수배(Constant Multiple)
g(x) = α ⋅ f(x)
- 함수의 출력값에 상수를 곱해주는 것을 의미 (여기서 α 는 상수를 의미)
- 상수배를 취한 함수는 원래 함수와 그래프의 모양은 동일하지만, y축 방향으로 늘어나거나 줄어들게 된다.
- 상수배는 함수의 크기를 조절할 때 매우 유용하게 사용
함수의 덧셈(Addition)
h(x) = f(x) + g(x)
- 두 함수를 합치는 연산 -> f(x)와 g(x)를 더하면 새로운 함수 h(x)가 생성
- 예를들어, f(x) = x^2이고 g(x) = x + 1이라면,
이 두 함수를 더하면 h(x) = f(x) + g(x) = x^2 + x + 1이 된다.
이차 및 삼차 함수
y = ax^2 + bx + c,
y = ax^3 + bx^2 + cx + d
- 이차 함수는 2차 다항식 함수로, 독립 변수 x의 최고 차수가 2인 함수이다.
- 일반적인 이차 함수의 형태는 y = ax^2 + bx + c이며, 여기서 a, b 및 c는 상수
- 계수 a는 포물선이 위로 열리는지 아래로 열리는지를 결정하며, 상수 b와 c는 꼭짓점의 위치와 x 및 y 축과의 교점을 결정한다.
- 이차 함수는 발사체의 궤적, 위성 안테나의 모양 또는 열기관의 효율성과 같은 다양한 물리적 현상을 모델링하는 데 자주 사용한다.
- 삼차 함수는 3차 다항식 함수로, 독립 변수 x의 최고 차수가 3인 함수
- 일반적인 삼차 함수의 형태는 y = ax^3 + bx^2 + cx + d이며, 여기서 a, b, c 및 d는 상수
- 삼차 함수는 이차 함수보다 더 복잡한 모양을 가지며, 두 개의 꼭지점 또는 변곡점을 가진다.
- 계수 a는 곡선의 전반적인 모양을 결정하며, 상수 b, c 및 d는 꼭지점 및 x 및 y 축과의 교점과 변곡점의 위치와 성격을 결정
- 삼차 함수는 유체 역학, 구조 역학 및 시장 동향과 같은 복잡한 현상을 모델링하기 위해 물리학, 공학 및 경제학 등의 다양한 분야에서 사용
유리함수(다항식의 비율로 나타낼 수 있는 함수)
f(x) = P(x) / Q(x)
- 여기서 P(x)와 Q(x)는 각각 다항식이며, Q(x)는 0이 아닌 상수항을 가지고 있다.
즉, 유리함수는 분모가 0이 되는 값을 제외하고는 모든 x에 대해 정의되는 함수이다. - 예를 들어, f(x) = (x^2 + 1) / (x - 3)는 유리함수이다.
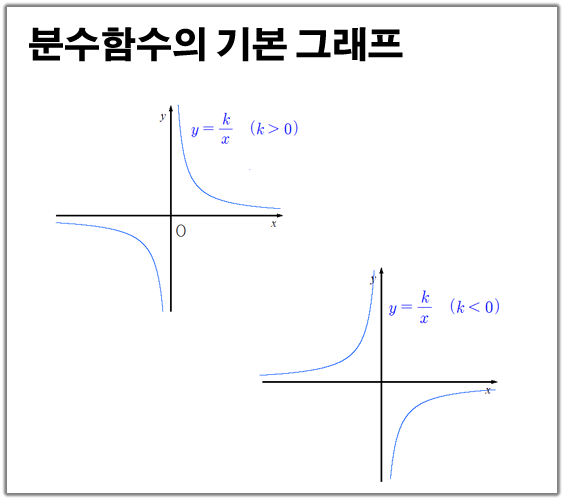
유리함수는 미적분학, 수학 물리학, 공학 및 통계학 등의 분야에서 중요하게 사용된다.
예를 들어, 통계학에서는 통계 모형의 오차 구조를 모형화할 때 유리함수를 사용한다.
무리함수(제곱근을 포함하는 함수)
f(x) = √(ax + b)
- 여기서 a와 b는 상수이며, x는 함수의 독립 변수이다.
- f(x) = √(x)의 경우, x는 0 이상의 실수여야만 한다.
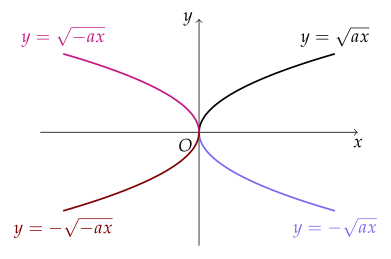
물리학에서는 무리함수를 사용하여 운동량-위치 관계나 에너지-위치 관계를 모델링한다.
또한, 금융 분야에서는 무리함수를 사용하여 이자율의 변화나 변동성을 모델링한다.
지수함수
f(x) = a^x
- a는 양수이면서 1이 아닌 상수이며, x는 함수의 독립 변수
- 지수함수에서 밑수 a는 양수이므로 함수값은 항상 양수이다.
- 지수함수는 x가 증가할수록 함수값이 기하급수적으로 증가하거나 감소한다.
- 지수함수는 미분 가능한 함수이며, 미분 결과도 다시 지수 함수 형태가 된다.
-> 이러한 특성으로 인해 지수함수는 최적화 문제나 변화율 문제를 해결하는 데에 유용하게 사용
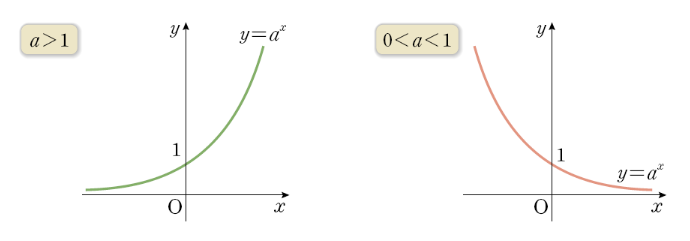
지수함수는 자연과학, 공학, 경제학 등 다양한 분야에서 사용된다.
예를 들어, 지수함수는 물리학에서 반감기나 전기적인 충전 및 방전 등에 대한 모델링에 사용
또한, 경제학에서는 지수함수를 사용하여 인구 성장, 이자 계산, 주식 시장 등을 모델링한다.
로그함수
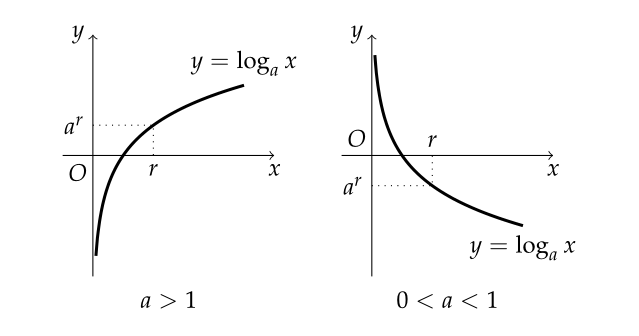
f(x) = log_a(x)
- a는 양수이면서 1이 아닌 상수이며, x는 함수의 독립 변수
- 로그함수에서 밑수 a는 양수이며, 함수값은 x가 양수일 때 음수가 될 수 없다.
- 로그함수는 지수함수의 역함수로 정의되며, 로그함수의 입력값 x는 밑수 a를 거듭제곱하여 만들 수 있는 값이다. ex) log_2(8) = 3은 2^3 = 8
- 로그함수도 지수함수와 마찬가지로 미분 가능한 함수이며, 미분 결과는 1/x * ln(a) 형태가 된다 -> 이러한 특성으로 인해 로그함수는 최적화 문제나 변화율 문제를 해결하는 데에 유용하게 사용
로그함수는 지수 함수와 마찬가지로 다양한 분야에서 사용된다.
예를 들어, 로그함수는 컴퓨터 과학에서 알고리즘 분석에 사용된다.
또한, 확률론에서는 로그함수를 사용하여 확률분포 함수의 곱셈을 덧셈으로 변환하여 계산한다.
삼각함수
f(x) = sin(x), f(x) = cos(x), f(x) = tan(x)
- 삼각함수의 기본공식
sin²θ + cos²θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = csc²θ
-
삼각함수의 부호
사분면 기준으로 각각의 삼각함수의 부호를 파악할 수 있다.
제 1사분면에서는 모든 함수가 양수이다.
제 2사분면에서는 사인함수만 양수이다.
제 3사분면에서는 탄젠트함수만 양수이다.
제 4사분면에서는 코사인함수만 양수이다. -
삼각함수의 짝수-홀수성
짝수함수 : cos(-θ) = cos(θ), 짝수(even)함수의 그래프는 y-축 대칭
홀수함수 : sin(-θ) = -sin(θ), 홀수(odd)함수의 그래프는 원점 대칭
탄젠트함수는 홀수함수가 아니므로 짝수성, 홀수성을 가지지 않음. -
삼각함수의 주요공식
1) 덧셈공식
sin(α + β) = sinαcosβ + cosαsinβ
cos(α + β) = cosαcosβ - sinαsinβ
tan(α + β) = (tanα + tanβ)/(1 - tanαtanβ)2) 차례로 빼기공식
sin(α - β) = sinαcosβ - cosαsinβ
cos(α - β) = cosαcosβ + sinαsinβ
tan(α - β) = (tanα - tanβ)/(1 + tanαtanβ)3) 이중각공식
sin2θ = 2sinθcosθ
cos2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ
tan2θ = (2tanθ)/(1 - tan²θ)4) 반각공식
sin(θ/2) = ±√[(1 - cosθ)/2]
cos(θ/2) = ±√[(1 + cosθ)/2]
tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]5) 쌍곡선 함수와 지수함수
sinh(x) = (e^x - e^(-x))/2
cosh(x) = (e^x + e^(-x))/2
tanh(x) = sinh(x)/cosh(x) = (e^x - e^(-x))/(e^x + e^(-x))
sech(x) = 1/cosh(x) = 2/(e^x + e^(-x))
csch(x) = 1/sinh(x) = 2/(e^x - e^(-x))
coth(x) = cosh(x)/sinh(x) = (e^x + e^(-x))/(e^x - e^(-x))
삼각함수의 이동 및 변환
-
수평 이동(horizontal shift)
y = f(x - c) : 함수 f(x)의 그래프를 오른쪽으로 c만큼 이동합니다.
y = f(x + c) : 함수 f(x)의 그래프를 왼쪽으로 c만큼 이동합니다. -
수직 이동(vertical shift)
y = f(x) + c : 함수 f(x)의 그래프를 위쪽으로 c만큼 이동합니다.
y = f(x) - c : 함수 f(x)의 그래프를 아래쪽으로 c만큼 이동합니다. -
축소/확대(scale)
y = a f(x) : 함수 f(x)의 그래프를 y축 방향으로 a배 만큼 축소 또는 확대한다.
a가 1보다 크면 확대, 1보다 작으면 축소한다.
y = f(bx) : 함수 f(x)의 그래프를 x축 방향으로 1/b배 만큼 축소 또는 확대한다.
b가 1보다 크면 축소, 1보다 작으면 확대한다. -
반전(reflection)
y = -f(x) : 함수 f(x)의 그래프를 x축에 대해 대칭하여 반전
y = f(-x) : 함수 f(x)의 그래프를 y축에 대해 대칭하여 반전
y = -f(-x) : 함수 f(x)의 그래프를 원점에 대해 대칭하여 반전
우함수와 기함수는 함수의 대칭성에 관한 속성
-
우함수(even function)는 다음을 만족하는 함수
f(-x) = f(x)
즉, 함수의 그래프가 y축 대칭인 함수
예를 들어, f(x) = x^2는 우함수이다.
왜냐하면, f(-x) = (-x)^2 = x^2 = f(x)이기때문에, 이 함수의 그래프는 y축 대칭이다. -
기함수(odd function)는 다음을 만족하는 함수
f(-x) = -f(x)
즉, 함수의 그래프가 원점 대칭인 함수
예를 들어, f(x) = x^3은 기함수이다.
왜냐하면, f(-x) = (-x)^3 = -x^3 = -f(x)이기때문에, 이 함수의 그래프는 원점 대칭이다.
- 우함수와 기함수는 다음과 같은 성질을 가집니다.
1) 두 우함수의 합은 우함수
2) 두 기함수의 합은 기함수
3) 우함수와 기함수의 곱은 기함수
동차성(Homogeneity), 가법성(Additivity), 선형성(Linearity)
- 함수의 입력값에 대한 스케일링과 조합에 따른 행동에 관련된 속성
-
동차성(또는 스케일링 속성)은 함수가 입력값의 스케일링에 대해 어떻게 행동하는지를 설명하는 속성
함수 f(x)가 k차 동차 함수라면 임의의 스칼라 α에 대해 f(αx) = α^k * f(x)가 성립
이것은 입력값 x를 α배로 스케일링하면 출력값 f(x)도 α^k배 만큼 스케일링됨을 의미 -
가법성(또는 중첩성 속성)은 함수가 입력값의 합에 대해 어떻게 행동하는지를 설명하는 속성
함수 f(x)가 가법 함수라면 임의의 두 입력값 x1과 x2에 대해 f(x1 + x2) = f(x1) + f(x2)가 성립
이것은 함수 f(x)가 각 입력값에 대해 개별적으로 반응하는 것과 동일한 방식으로 결합된 입력값에 반응함을 의미 -
선형성(Linearity)은 동차성과 가법성의 결합
함수 f(x)가 동차성과 가법성 모두를 만족하면 선형 함수라고 한다.
즉, 임의의 스칼라 α와 β와 임의의 입력값 x1과 x2에 대해 f(αx1 + βx2) = αf(x1) + βf(x2)가 성립
이것은 입력값의 스케일링과 합에 대한 효과가 독립적이고 예측 가능하다는 것을 의미
선형 함수의 정의
f(x) = ax
f(αx1 + βx2) = αf(x1) + βf(x2)
-
f(x) = ax라는 함수가 주어졌을 때, a는 상수이며 x는 변수
이 함수는 x에 대해 1차 함수(직선)의 형태를 가지며, 그래프는 원점을 지나는 직선이다. -
또한, f(αx1 + βx2) = αf(x1) + βf(x2)는 선형 함수의 중요한 성질 중 하나
이를 선형성(linearity)이라고 한다.
이 성질은 함수가 스칼라곱과 합의 분배법칙을 만족한다는 것을 의미
즉, 함수의 입력값이 αx1 + βx2라면, 이를 x1과 x2의 가중합으로 나타내어 f(x1)과 f(x2)의 가중합으로 분해할 수 있다. 이때 가중치는 α와 β
함수 g(x) = ax + b는 선형이 아닌 어파인 함수
-
이 함수는 동차성 (또는 스케일링 특성)을 만족하지만 가법성 (또는 중첩 특성)을 만족하지 않는다.
어파인 함수에서는 입력값에 상수를 곱하면, 출력값도 상수만큼 변한다. -
g(x) = ax + b
g(αx1) = a(αx1) + b = α(ax1) + b = α(ax1) + b >>> x에 αx1 대입한 결과α g(x1) = α(ax1 + b) = α(ax1) + αb
위 두 식의 결괏값은 동일하지 않다.
