마구간 정하기(결정알고리즘)

문제

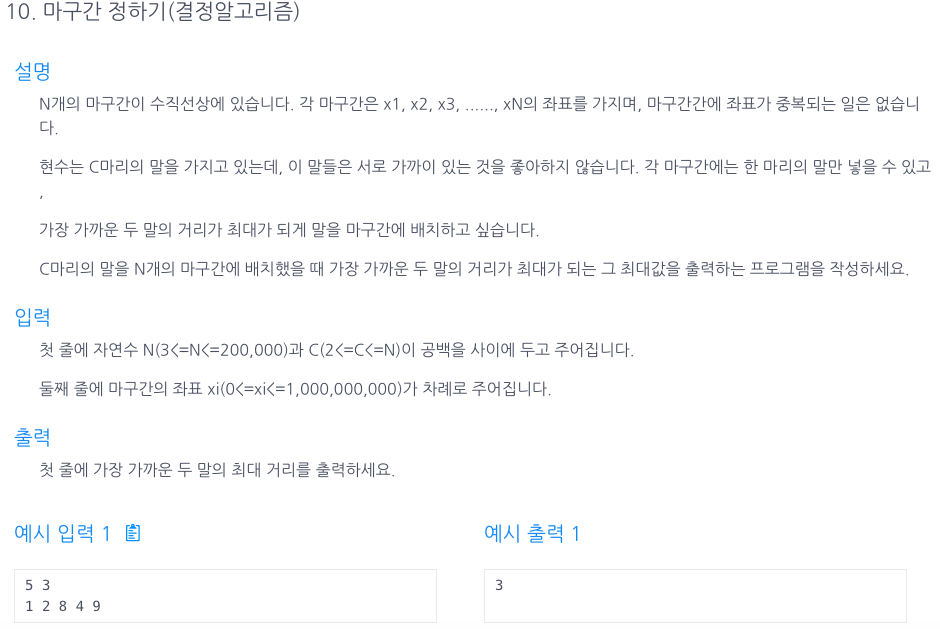
나의풀이

import java.util.*;
class Main {
	//들어갈수있는 말 마릿수
	public int Count(int[] arr, int distance) {
		int cnt = 0;
		int ep = 0;
		for(int i=0; i<arr.length;i++) {
			//첫번째 말
			if(i == 0) {
				cnt++;
				ep = arr[i];
			}
			if(i>0 && arr[i]-ep >= distance) {
				cnt++;
				ep = arr[i];
			}
		}
		return cnt;
	}
	public int solution(int n, int c,int[] arr) {
		//n 마구간의 갯수/ c 말의 갯수/ arr 마구간좌표
		int answer = 0;
		Arrays.sort(arr);
		//lt = 거리의 최솟값이 될수있는값. rt = 거리의 최댓값이 될수있는값.
		int lt = 1, rt = arr[n-1];
		while(lt<=rt) {
			int mid = (lt+rt)/2;
			if(Count(arr, mid) >= c) {
				answer = mid;
				lt = mid +1;
			}
			else rt = mid -1;
		}
		
		return answer;
	}

		    
	public static void main(String[] args) {
		Main T = new Main();
		Scanner kb = new Scanner(System.in);
		int n = kb.nextInt();
		int m = kb.nextInt();
		int[] arr = new int[n];
		for(int i=0; i<n; i++) arr[i] = kb.nextInt();
		System.out.print(T.solution(n, m, arr));
	}
	
}

++ Count함수 요약

	public int Count(int[] arr, int distance) {
		int cnt = 0;
		int ep = arr[0];
		for(int i=1; i<arr.length;i++) {
			if(i>0 && arr[i]-ep >= distance) {
				cnt++;
				ep = arr[i];
			}
		}
		return cnt;
	}

풀이방법

전 문제와 비슷하듯 다른듯하다..
lt를 마구간 사이의 거리가 될 수 있는 최솟값인 1로두고,
rt를 마구간 사이의 거리가 될 수 있는 arr의 젤 끝 원소로 지정해줬다.

mid((lt+rt)/2) 값부터 탐색을 시작해서 mid거리 만큼 갭을 두고 말을 두면 최대 몇마리의 말을 둘 수 있는지 return하는 Count함수를 만들었다.

첫번째 말은 항상 제일 작은 좌표에 담겨야하므로 cnt = 1부터 시작하고
ep(바로 직전 말이 들어간 마구간좌표)는 arr[0] 부터 시작된다.

만약 (현재 마구간의 좌표) - (바로 직전 말이 있는 좌표) = 직전 말과의 거리
가 distance보다 크거나 같다면 그 말은 현재 마구간에 들어갈 수 있으므로
cnt++ 되고 ep는 현재 마구간 좌표로 바뀐다.

만약, 말의 마구간에 들어간 말의 마릿수가 c(타겟넘버)보다 크거나 같다면, 거리가 더 늘어나도 된다는 의미이므로 mid보다 더 작은값은 탐색이 필요없으므로 lt = mid+1이 되고,

그렇지않고, c보다 작다면 거리가 너무 크다는 의미이므로 mid보다 더 큰 값은 탐색이 필요없으므로 rt = mid-1이 된다.

while문이 돌면서 answer에 최대거리를 저장하게 된다.

핵심키워드

아직까지 lt와 rt값을 어떤값으로 시작해야할지 감이 잘 안온다...
결정알고리즘을 이용한 더 다양한 문제를 풀어봐야겠다!