프롤로그
자료구조 에서 heap이 뭔지, 특성은 무엇인지 알아보기 위한
개인 공부개념으로 블로그를 작성했으며, 문제시 수정하겠습니다!
힙(heap)
힙(heap)은 트리 기반의 자료구조로, 특정한 규칙을 만족하는 완전 이진트리이다. 힙은 주로 우선순위 큐를 구현하는 데 사용된다.
힙의 특성
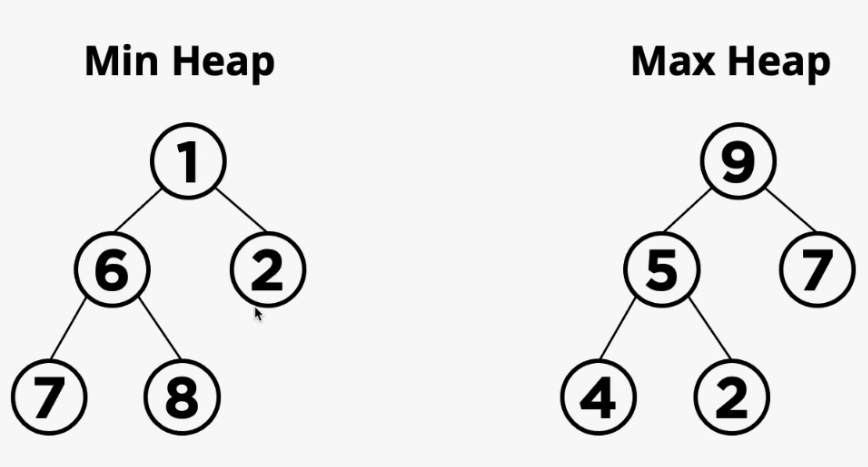
힙은 최대 힙 Max Heap 과 최소 힙 Min Heap 으로 구분할 수 있다. 최대 힙은 부모노드가 항상 자식 노드보다 큰 값을 가지고 있기 때문에 루트 노드는 항상 트리의 최대값을 가지고 있게 된다. 반대로 최소 힙은 부모노드의 값은 항상 자식 노드보다 작기 때문에, 루트 노드는 트리의 최소값이 된다. 따라서, 이 힙의 새로운 값이 추가되거나 삭제되어도 특성이 유지된다.
출처: https://rosweet-ai.tistory.com/60
힙은 이진탐색트리와는 다르게 값의 중복을 허용하고, 이진탐색트리에서는 왼쪽 오른쪽 기준으로 작은값과 큰 값에 대한 제약이 존재한다면, 힙은 좌우 노드간에는 값의 제약이 없고 상하 관계에서만 값의 제약을 받는다.
min heap 과 max heap인 위의 그림을 보면, 왼쪽은 루트에 최소값 1을 가진 min heap인 것을 알 수 있다. 루트1의 자식인 6과 2는 둘다 부모노드보다 큰 값이고, 6노드의 자식 노드들도 모두 6보다 큰 값인 것을 알 수 있다.
오른쪽 그림은 가장 큰 값이 9를 가진 max heap 이다. 자신보다 작은 값인 5와 7이 루트노드의 자식으로 있으며, 5의 자식들도 5보다 작은 4와 2가 들어있다.
그림을 토대로, 위아래가 아닌 좌우 노드간에 크기관계는 제약이 없는 것을 확인할 수 있다.
시간복잡도
힙(heap)은 자료구조에서 최대 혹은 최소값을 빠르게 가져오는게 중요한 상황에서 사용할 수 있다.
힙에서 최대 혹은 최소값은 항상 루트노드에 있기 때문에, 시간 복잡도는 0(1) 상수값으로 찾을 수가 있다. 찾는 연산과는 다르게 데이터의 삽입과 삭제는 0(logN)의 값을 갖는데 왜 그럴까
응용
힙의 대표적인 응용에는 우선순위 큐 가 있다.
일반적인 큐는 먼저 들어온 데이터가 먼저 나가는 FIFO(First In First Out)의 데이터 구조이다. 우선순위 큐는 데이터가 들어온 순서와 상관없이 우선순위가 높은 데이터 순으로 처리하는 구조이다.
ex) 운영체제의 작업 스케쥴링
우리가 처리할 일이 있으면, 일의 중요도에 따라서 먼저 처리하는 것처럼 컴퓨터도 비슷한 과정으로 task를 처리한다.
용어 정리
- Queue
큐는 '선입선출' , FIFO(First In First Out)의 개념을 가진 선행 자료구조이다. 스택은 입구와 출구가 동일하여 나중에 들어온 순서대로 나가는 구조지만, 큐는 입구와 출구가 달라 먼저 들어온 데이터가 먼저 나가는 구조이다.
힙 정렬(Heap sort)
https://rosweet-ai.tistory.com/60
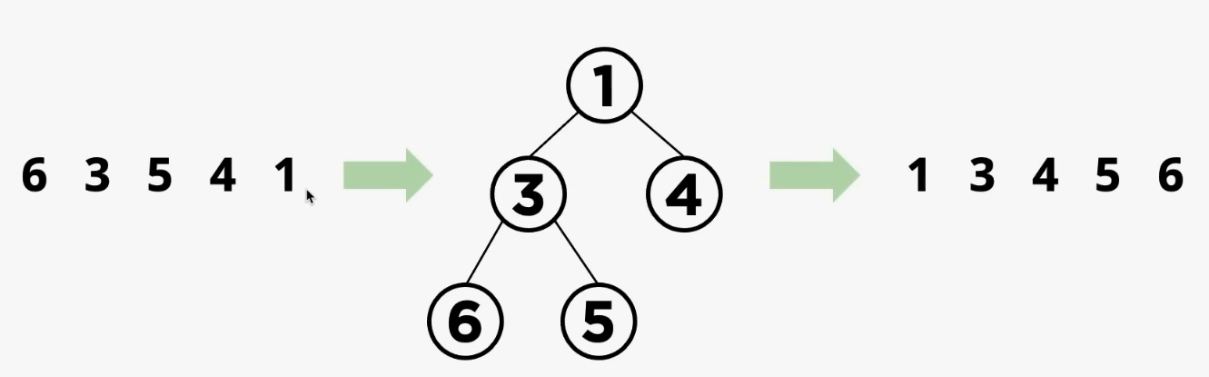
우선순위 큐 말고도 자료구조 힙의 특성을 이용한 힙 정렬이 있다. 왼쪽처럼 정렬되지 않은 데이터가 무작위의 순서로 주어지면 주어진 데이터로 힙을 구성하게 된다. 가운데 min heap 이 구성된 것을 볼 수 있다. 여기서 루트의 값을 가져오는 pop연산을 수행하면 항상 힙에 있는 최소값이 출력되서, 데이터가 순서대로 정렬된 결과를 얻을 수가 있다. 만약 max heap 을 구성하면 내림차순된 결과를 얻을 수 있다.
힙을 배열로
힙은 완전 이진트리이기 때문에, 중간에 빈 값이 없는 1차원 배열로 표현이 가능하다.
이때 배열의 0번째 인덱스부터 채우게 되지만, 노드탐색의 용이성 때문에, 보통 1번 인덱스부터 루트값을 채운다. 특정 인덱스에 위치한 노드의 부모노드는 자신의 인덱스를 2로 나눈 인덱스에서 찾을 수 있고, 왼쪽 자식노드는 자신의 인덱스 곱하기2, 오른쪽 자식노드는 인덱스에 곱하기 2+1의 위치에 존재한다.
힙의 연산 Heapify
출처:https://rosweet-ai.tistory.com/60
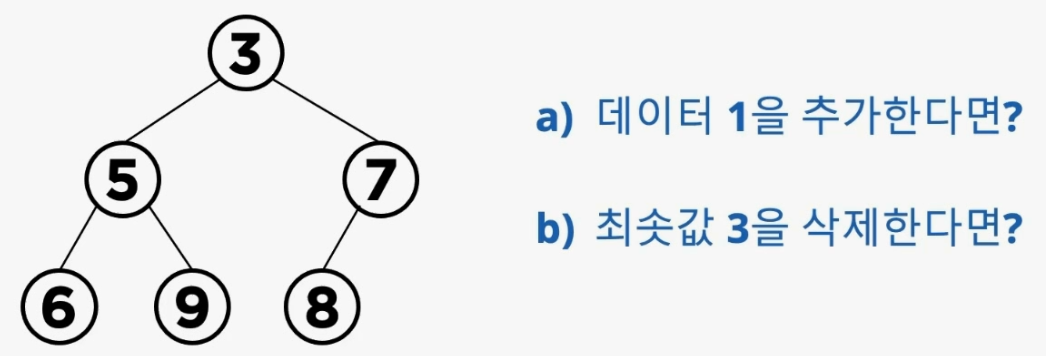
힙에서 가장 핵심이 되는 연산은 Heapify 이다.
힙의 데이터가 추가되거나, 삭제가 될 경우 힙의 데이터 최대힙(max heap), 최소힙(min heap)의 속성은 유지되어야 한다.
위의 그림과 같이 min heap이 있을 경우, 루트값보다 더 작은 데이터 1을 힙에 삽입하려고 하면 min heap 의 루트값이 바뀌면서 하위의 트리 구조도 다시 재구조화가 필요하다. 또한 min heap의 최소값인 루트 노드의 3 값을 삭제할 경우, 루트 노드를 채워주며 min heap 이 유지되어야 한다.
이렇게 힙을 재구조화 해주는 연산을 heapify 라고 한다.
데이터 삽입
출처: https://rosweet-ai.tistory.com/60
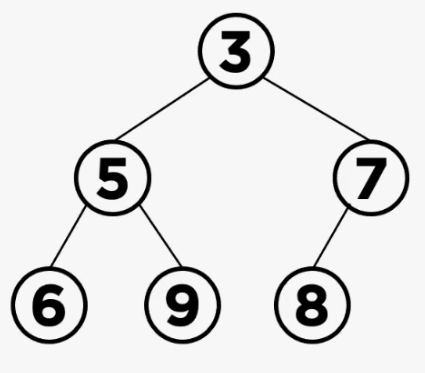
먼저 최소힙(min heap)에서 데이터가 삽입될 경우, 힙 내부에서 어떻게 처리되는지 알아보자.
ex) min heap에서 데이터 1을 min heap의 추가할 경우
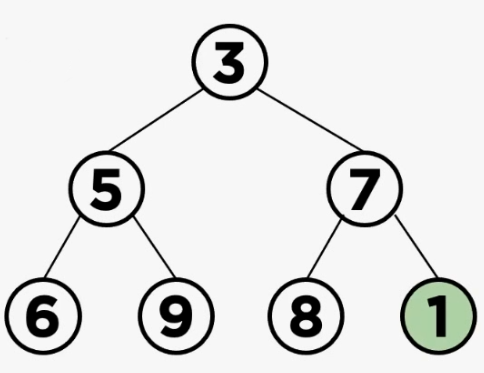
출처: https://rosweet-ai.tistory.com/60
(1) leaf 노드의 데이터 삽입
힙은 완전이진트리의 형태를 유지해야하기 떄문에, leaf 노드에 제일 먼저 데이터를 삽입하게 된다. 이 트리에서 완전 이진트리 형태를 유지하는 leaf 노드의 위치는 데이터 7의 오른쪽 자식 노드가 된다. 따라서 먼저 leaf 노드에 데이터를 삽입한 후 min heapdml 조건을 만족하는 지 확인한다.
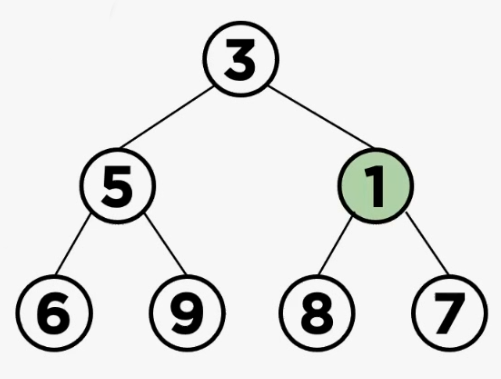
출처: https://rosweet-ai.tistory.com/60
(2) 삽입된 노드를 부모 노드와 바꿔주는 연산 진행
최소힙(min heap)의 조건을 충족하면 추가적인 연산을 할 필요없이 삽입 연산을 바로 종료한다. 그러나 지금의 경우 추가된 노드가 min heap의 조건을 만족하지 못하기 때문에, 삽입된 노드를 부모 노드와 바꿔주는 연산을 진행한다.
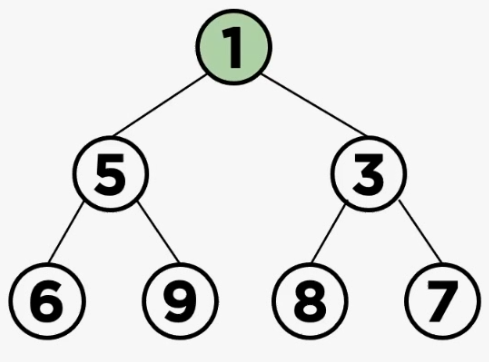
출처: https://rosweet-ai.tistory.com/60
(3) 여기서 최소힙의 조건을 충족하면 삽입 연산 종료
=> 삽입 연산시 우선 leaf 노드에 데이터를 추가하고, 다음에 추가돈 노드가 heap의 조건을 만족하는지 확인 후 힙의 조건을 만족할 때까지 부모노드와 값을 바꾸는 동작을 계속 진행하게 된다. max heap도 부등호의 방향만 반대로 바뀌고 동일한 방법으로 데이터의 삽입이 이루어진다.
데이터 삭제
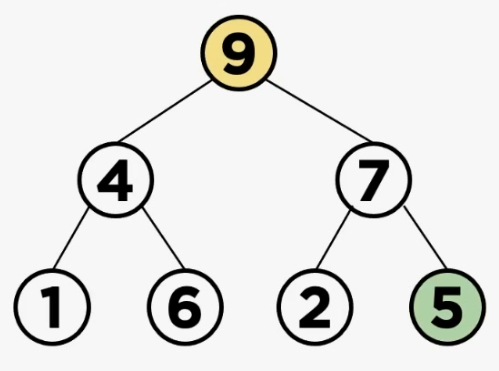
출처: https://rosweet-ai.tistory.com/60 맥스힙의 예시
이번에는 힙에서 데이터의 삭제 연산을 확인해보자.
힙은 최소값이나 최대값을 빠르게 찾기위한 자료구조이기 때문에, 최소힙이든 최대힙이든 루트 노드에서만 삭제연산이 이뤄지는 케이스이다. 이번에는 max heap으로 알아보자
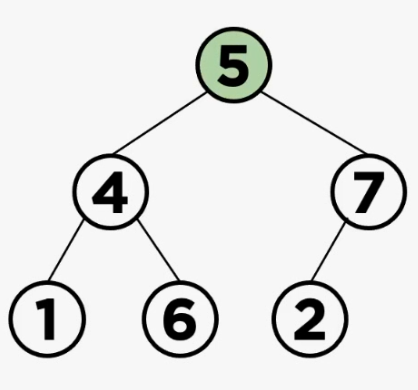
출처: https://rosweet-ai.tistory.com/60
(1) leaf 노드의 데이터 삽입
완전 이진트리가 유지되어야하는 조건은 동일하기에, 완전 이진트리의 가장 마지막에 위치한 노드를 루트로 가지고 오면서 마지막 노드를 삭제한다. 그러면 아래와 같은 그림 모양으로 max heap의 값이 변경된다.
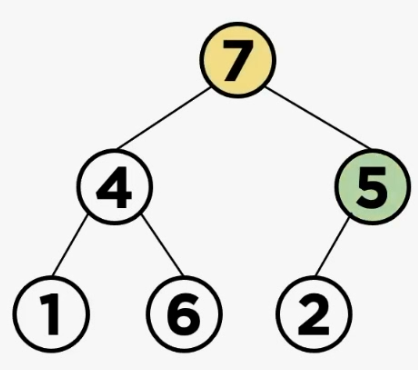
출처: https://rosweet-ai.tistory.com/60
(2) 삽입된 데이터를 자식 노드와 위치 교환
이 상태에서 삽입할 때와 동일하게 힙 조건을 만족하는지 확인 후, 만족하지 않는다면, 자식노드와 위치를 바꿔주면 된다. 삽입할 때는 부모노드와 자리를 바꾸었다면 삭제할 때는 자식 노드와 자리를 바꿔가면서 heapify의 연산을 한다고 보면 된다.
시간복잡도
힙에서 최소값 혹은 최대값을 찾는 연산은 루트에 있는 값만 가져오면 되서, 시간복잡도는 O(1)이다. 하지만 힙에서 데이터의 삽입과 삭제 과정에서는 이진트리에 데이터가 N개가 있을때 1/2씩 인덱스를 줄여나가면서 자신의 위치를 찾기 때문에 시간복잡도는 logN이 된다.

